Zusammenfassung – Wahrscheinlichkeitsmodelle
Von der Realität zum Modell
Wahrscheinlichkeiten werden immer von Menschen gesetzt. Sie sind mathematische Modelle, die passend zu realen Situationen erschaffen werden.
Im Fall eines Standardwürfels wird in der Regel von der Annahme ausgegangen, dass er fair ist und alle Augenzahlen mit gleicher Chance fallen. Das spiegelt sich in der Setzung $P(e) = \frac{1}{6}$ für alle möglichen Ergebnisse $e$ beim Würfelwurf wider.
Wenn wie beim Pyramidenwürfel keine sinnvolle Annahme möglich ist, dann wird eine längere Versuchsreihe durchgeführt und mit Hilfe der ermittelten relativen Häufigkeiten die gesuchten Wahrscheinlichkeiten geschätzt. Solche Schätzungen sind unsicher.
Vom Modell zur Realität
Modelle müssen sich in der Realität bewähren.
Bei einem Standardwürfel werden in einer langen Versuchsreihe relative Häufigkeiten erwartet, die den Wahrscheinlichkeiten entsprechen. Gibt es hier größere Abweichungen, dann gibt es Zweifel, ob der Würfel tatsächlich fair ist. Mit weiteren Versuchsreihen und entsprechenden Berechnungen muss das dann geklärt werden. Wir werden das in einem weiteren Kapitel durchspielen.
Wenn die Wahrscheinlichkeiten mit Hilfe einer Schätzung gesetzt wurden, dann sind diese Werte von Beginn an eher unsicher. Gegebenenfalls müssen sie – wenn neue Daten oder Erkenntnisse vorliegen – nochmal nachjustiert werden.
Präzisierung von Wahrscheinlichkeitsmodellen
Einschätzung zu realen Situationen werden meist informell in unserer gängigen Umgangssprache formuliert. Mathematische Modelle werden dagegen immer möglichst präzise in der Sprache der Mathematik beschrieben. Hierfür werden dann spezielle Fachbegriffe und Schreibweisen verwendet. Die folgenden Beispiele verdeutlichen die Verwendung dieser unterschiedlichen Sprachen.
Beispiel: Standardwürfel-Modell
| Realität | Modell | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Zufallsexperiment: einen Standardwürfel werfen und dabei die Augenzahl beobachten |
|||||||||||||||
| Ergebnisse: 1: Augenzahl 1 2: Augenzahl 2 ... |
Ergebnismenge: $\Omega = \{1, 2, 3, 4, 5, 6\}$ |
||||||||||||||
| Wahrscheinlichkeitsannahme: Alle Ergebnisse sind gleichwahrscheinlich. |
Wahrscheinlichkeitsfunktion:
|
Beispiel: Pyramidenwürfel-Modell
| Realität | Modell | ||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Zufallsexperiment: einen Pyramidenwürfel werfen und dabei die Augenzahl beobachten |
|||||||||||||||||||||||||||||
| Ergebnisse: 1: Augenzahl 1 2: Augenzahl 2 ... |
Ergebnismenge: $\Omega = \{1, 2, 3, 4, 5, 6\}$ |
||||||||||||||||||||||||||||
| Wahrscheinlichkeitsschätzung: Die Wahrscheinlichkeiten werden ausgehend von den relativen Häufigkeiten aus einer langen Versuchsreihe gesetzt.
|
Wahrscheinlichkeitsfunktion:
|
Die Beispiele zeigen, dass wir ein Wahrscheinlichkeitsmodell mit einer Ergebnismenge und einer Wahrscheinlichkeitsfunktion beschreiben.
Die Ergebnismenge zu einem Zufallsexperiment ist die Menge aller möglichen Ergebnisse des Zufallsexperiments.
Beachte, dass bei der Festlegung der Ergebnismenge immer genau berücksichtigt werden muss, was beim Zufallsexperiment beobachtet wird. Zur Darstellung einer Ergebnismenge benutzen wir in der Regel den griechischen Buchstaben $\Omega$ (Omega).
Eine Wahrscheinlichkeitsfunktion ist eine Funktion $P$, die jedem Ergebnis $e \in \Omega$ eine Wahrscheinlichkeit $P(e)$ zuordnet. Dabei müssen folgende Bedingungen erfüllt sein:
- $P(e)$ ist für alle $e \in \Omega$ eine reelle Zahl aus dem Intervall $0 \leq x \leq 1$.
- Die Summe aller Wahrscheinlichkeiten $P(e)$ für $e \in \Omega$ muss den Wert $1$ ergeben.
Eine Wahrscheinlichkeitsfunktion legt eine Wahrscheinlichkeitsverteilung über der Ergebnismenge fest. Eine solche Wahrscheinlichkeitsverteilung kann grafisch mit einem Histogramm veranschaulicht werden.
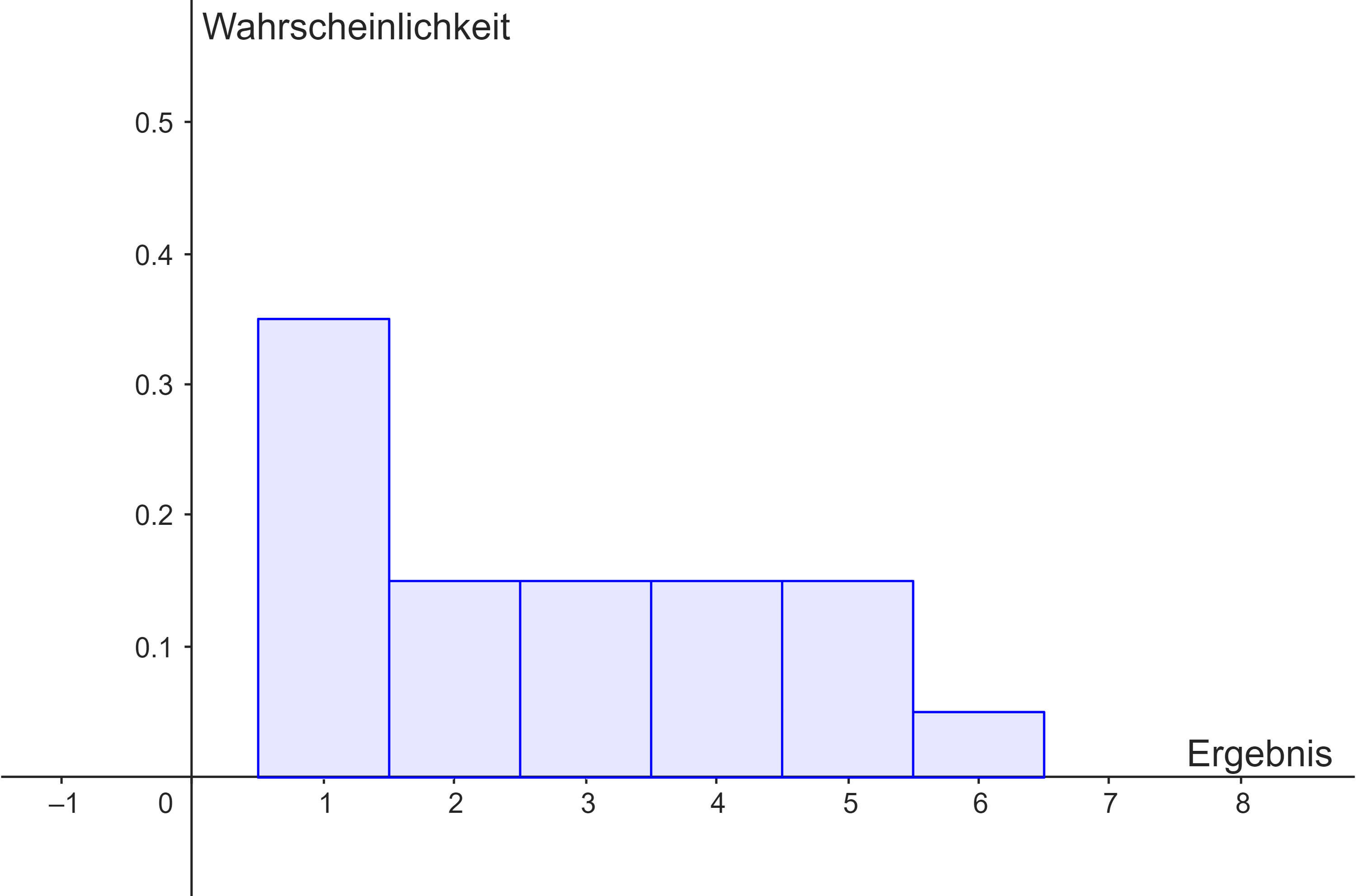
Ein Wahrscheinlichkeitsmodell zu einem Zufallsexperiment besteht aus einer Ergebnismenge $\Omega$ und einer zugehörigen Wahrscheinlichkeitsfunktion $P$.
Laplace-Experimente
Besonders einfach sind Wahrscheinlichkeitsmodelle, bei denen vorausgesetzt wird, dass alle Ergebnisse gleichwahrscheinlich sind. Zufallsexperimente mit dieser Eigenschaft werden Laplace-Experimente (nach dem französischen Mathematiker Pierre-Simon Laplace, der von 1749 bis 1827 lebte) genannt.
Ein Laplace-Experiment ist ein Zufallsexperiment, bei dem alle Ergebnisse gleichwahrscheinlich sind.
Das Zufallsexperiment „einen Standardwürfel werfen und dabei die Augenzahl beobachten“ ist ein Laplace-Experiment. Das Zufallsexperiment „einen Pyramidenwürfel werfen und dabei die Augenzahl beobachten“ ist dagegen kein Laplace-Experiment.
Bei einem Laplace-Experiment mit $n$ Ergebnissen wird die Wahrscheinlichkeit folgendermaßen festgelegt:
$P(e) = \frac{1}{n}$ für alle Ergebnisse $e$ aus der Ergebnismenge $\Omega$.

