Erarbeitung – Wahrscheinlichkeiten
Wahrscheinlichkeiten von Ergebnissen bestimmen
Wir betrachten weiterhin das folgende Zufallsexperiment:
Ein Würfel wird genau 3-mal geworfen. Dabei wird beobachtet, ob bei den einzelnen Würfen eine 6 oder keine 6 fällt.
Wir bearbeiten jetzt folgende Fragestellung:
Leitfrage
Wie erhält man die Wahrscheinlichkeiten der einzelnen Ergebnisse bei diesem Zufallsexperiment?
Die Idee ist, sich vorzustellen, dass das Zufallsexperiment sehr oft durchgeführt wird.
Aufgabe 1 – Wahrscheinlichkeiten der jeweiligen Würfe
(a) Trage in einem ersten Schritt die Wahrscheinlichkeiten der jeweiligen Würfe in das Baumdiagramm ein.
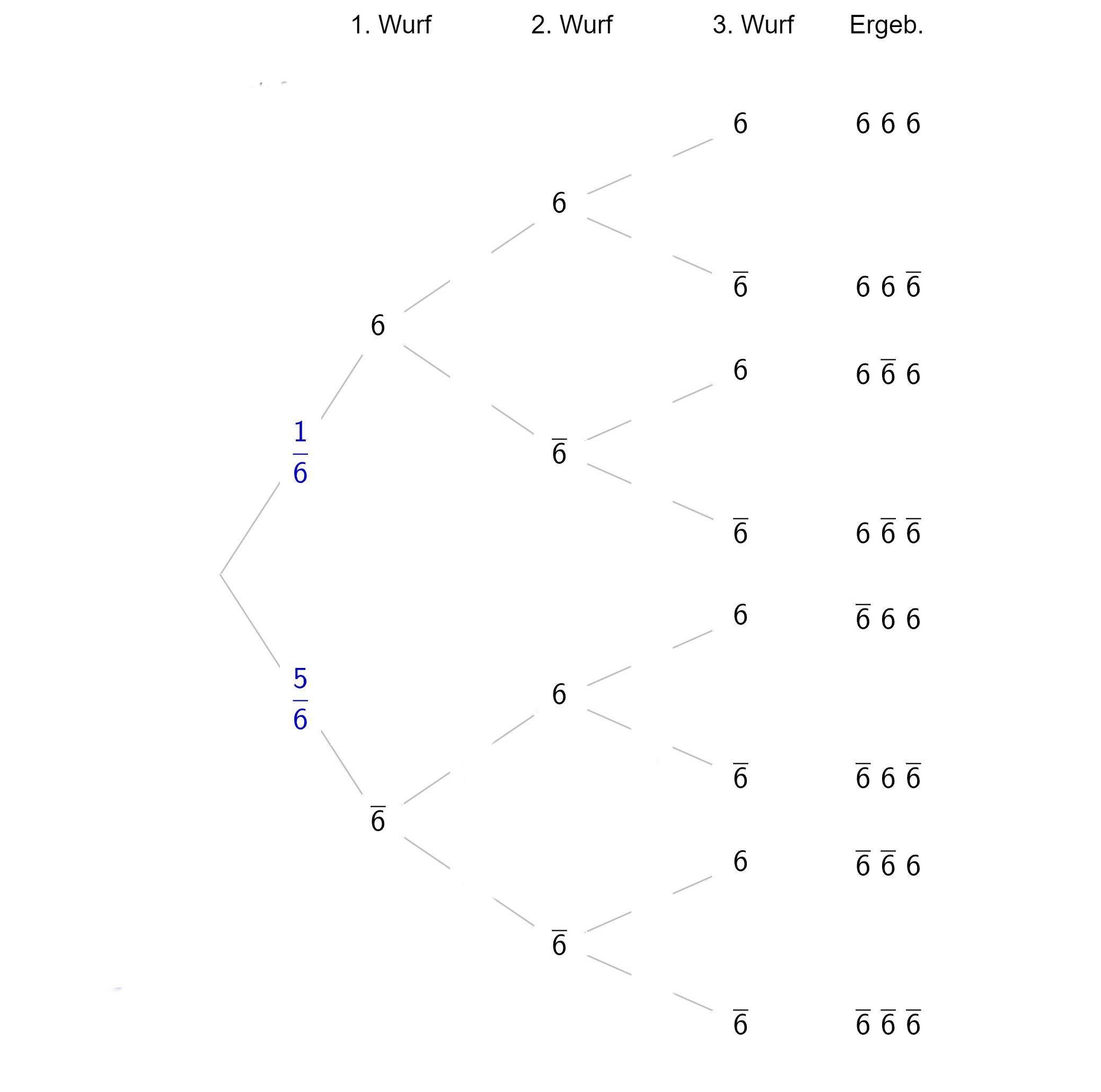
(b) Benutze zunächst das GeoGebra-Applet, um die Wahrscheinlichkeitsangaben in Aufgabe (a) zu kontrollieren:
(c) Wenn du alle Stufen des Zufallsexperiments angezeigt hast, dann kannst du zusätzlich einen Schieberegler einblenden, mit dem
eine Wiederholungszahl $n$ festgelegt werden kann, die angibt, wie oft das Zufallsexperiment 3-mal würfeln
(in Gedanken) durchgeführt werden soll. (Die Zahlen, die für $n$ eingestellt werden können, wirken zunächst etwas merkwürdig. Sie sind so gewählt, dass die Rechnungen einfache Zahlenwerte liefern).
Stelle die Wiederholungszahl $n$ auf den höchsten Wert $n = 2160$ ein. Notiere an jeder Verzweigung und am Pfadende, wie oft dieser Fall idealerweise auftritt.
Wenn du Hilfe benötigst, dann schaue dir die Berechnungen für ein Ergebnis hier an:
Hilfe
Zum Herunterladen: haeufigkeiten.ggb
Die berechneten Häufigkeiten kannst du hier kontrollieren:
Kontrolle
Zum Herunterladen: baum_3malwuerfeln_3.ggb
Aufgabe 2 - Wahrscheinlichkeiten festlegen
Die Wahrscheinlichkeit eines Ergebnisses beschreibt die erwartete relative Häufigkeit des Ergebnisses bei einer langen Versuchsreihe.
Wir nutzen die Überlegungen und Berechnungen aus Aufgabe 1, um die Wahrscheinlichkeiten beim Zufallsexperiment 3-mal würfeln
festzulegen.
(a) Beschreibe und erkläre mit Hilfe des folgenden GeoGebra-Applets ein Verfahren, mit dem man die Wahrscheinlichkeit eines
Ergebnisses beim Zufallsexperiment 3-mal würfeln
erhält.
Zum Herunterladen: pfadregel.ggb
Beim betrachteten Zufallsexperiment erhält man die Wahrscheinlichkeit eines Ergebnisses, indem man ....
(b) Bestimme analog die Wahrscheinlichkeiten aller Ergebnisse beim Zufallsexperiment 3-mal würfeln
.
Die ermittelten Wahrscheinlichkeiten kannst du hier kontrollieren:
Kontrolle
Zum Herunterladen: baum_3malwuerfeln_4.ggb
