Erarbeitung – Ergebnisse
Die möglichen Ergebnisse beschreiben
Wir betrachten das folgende Zufallsexperiment:
Ein Würfel wird genau 3-mal geworfen. Dabei wird beobachtet, ob bei den einzelnen Würfen eine 6 oder keine 6 fällt.
Wir wollen zunächst alle Möglichkeiten aufschreiben. Das können wir in der folgenden Form tun:
- ${\overlinepatch{6}}\,{\overlinepatch{6}}\,6$:
Beim 1. Wurf und 2. Wurf keine 6 und beim 3. Wurf eine 6.
Leitfrage
Wie notiert und wie erhält man die Ergebnisse bei diesem Zufallsexperiment?
Aufgabe – Bestimmung aller Ergebnisse
(a) Probiere zunächst selbst, alle möglichen Ergebnisse des oben beschriebenen Zufallsexperiments zu ermitteln. Vervollständige hierzu die Ergebnismenge:
$\Omega=\{\,6\,6\,6,~ 6\,6\,{\overlinepatch{6}},~ ...\}$
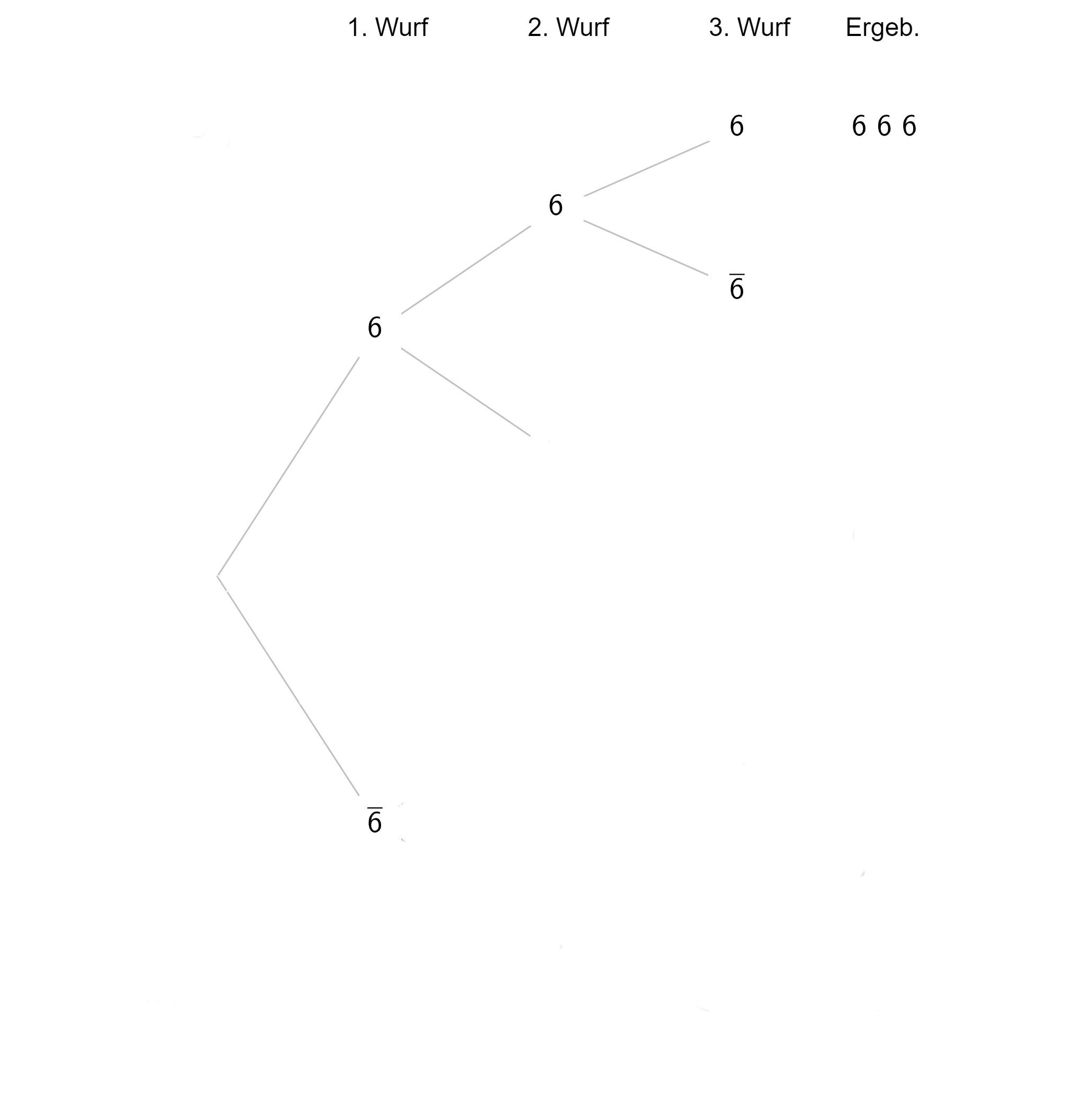
(b) Kontrolliere deine Ergebnisse, indem du ein Baumdiagramm erstellst.
💡 Tipp
Das Baumdiagramm erfasst die Ergebnisse systematisch:
Hier findest du die Lösung zur Selbstkontrolle.
Zusatzaufgabe – Beschreibung der Ergebnisse
Es gibt viele Möglichkeiten ein Ergebnis bei dem oben dargestellten Zufallsexperiment zu beschreiben.
Beurteile die folgenden Vorschläge mit Einschätzungen wie z.B. (gut) geeignet
, (eher) ungeeignet
:
- $(1, 4, 6)$:
Beim 1. Wurf die Augenzahl 1, beim 2. Wurf die Augenzahl 4 und beim 3. Wurf die Augenzahl 6. - $146$:
Beim 1. Wurf die Augenzahl 1, beim 2. Wurf die Augenzahl 4 und beim 3. Wurf die Augenzahl 6. - $(\overlinepatch{6} , \overlinepatch{6} , 6)$:
Beim 1. Wurf und 2. Wurf keine 6 und beim 3. Wurf eine 6. - ${\overlinepatch{6}} - {\overlinepatch{6}} - 6$:
Beim 1. Wurf und 2. Wurf keine 6 und beim 3. Wurf eine 6. - $\overlinepatch{6} ~ \overlinepatch{6} ~ 6$:
Beim 1. Wurf und 2. Wurf keine 6 und beim 3. Wurf eine 6.
