Zusammenfassung – Wahrscheinlichkeiten und relative Häufigkeiten
Zufallsexperimente
Der Begriff „wahrscheinlich“ wird immer dann verwendet, wenn in einer Situation unklar ist, welches Ergebnis eintritt.
Beispiele
- Beim Werfen eines Würfels ist unklar, welche Augenzahl fällt.
- Bei einer Wettervorhersage ist es heute noch nicht ganz klar, ob es in genau einer Woche an einem bestimmten Ort gegen 12 Uhr regnet.
- Bei einer Flugreise ist es unklar, ob alle gebuchten Flüge auch tatsächlich angetreten werden.
- Bei einer Befragung einer unbekannten Person ist es unklar, welche Antwort diese Person ankreuzen wird.
- ...
Solche Situationen werden mit dem Begriff Zufallsexperiment beschrieben.
Ein Zufallsexperiment (oder Zufallsversuch) ist ein Vorgang, ...
- ... bei dem mehrere Ergebnisse möglich sind,
- ... bei dem vorab aber nicht genau vorhergesagt werden kann, welches Ergebnis tatsächlich eintritt,
- ... der unter gleichen Bedingungen beliebig oft wiederholt werden kann.
Dabei spielt es für uns keine Rolle, warum keine eindeutige Vorhersage möglich ist. Das kann auf Erscheinungen beruhen, die uns zufällig vorkommen, oder auch auf Unwissenheit.
Empirisches Gesetz der großen Zahlen
Wenn ein Zufallsexperiment einmalig durchgeführt wird, kann das Eintreffen eines Ergebnisses nicht vorhergesagt werden. Wenn das Zufallsexperiment dagegen wiederholt durchgeführt wird, zeigen sich Stabilisierungseffekte.
Beispiele
- Wenn oft gewürfelt wird, dann kommen alle Augenzahlen etwa gleich oft vor.
- Bei einer bestimmten Wetterlage beträgt die Regenwahrscheinlichkeit 90%.
- Erfahrungen zeigen, dass 99% aller gebuchten Flüge von ... nach ... auch angetreten werden.
- Wenn viele Personen befragt werden, dann ergibt sich ein Meinungsbild.
- ...
Dieses Stabilisierungsphänomen lässt sich auch experimentell bestätigen. Hierzu wird die relative Häufigkeit der Ergebnisse betrachtet.
$\text{relative Häufigkeit} = \displaystyle\frac{\text{absolute Häufigkeit}}{\text{Anzahl der Wiederholungen}}$
Die Abbildung verdeutlicht diesen Stabilisierungseffekt für das Eintreffen der Augenzahl 1 beim 100-maligen Würfeln mit einem Standardwürfel.
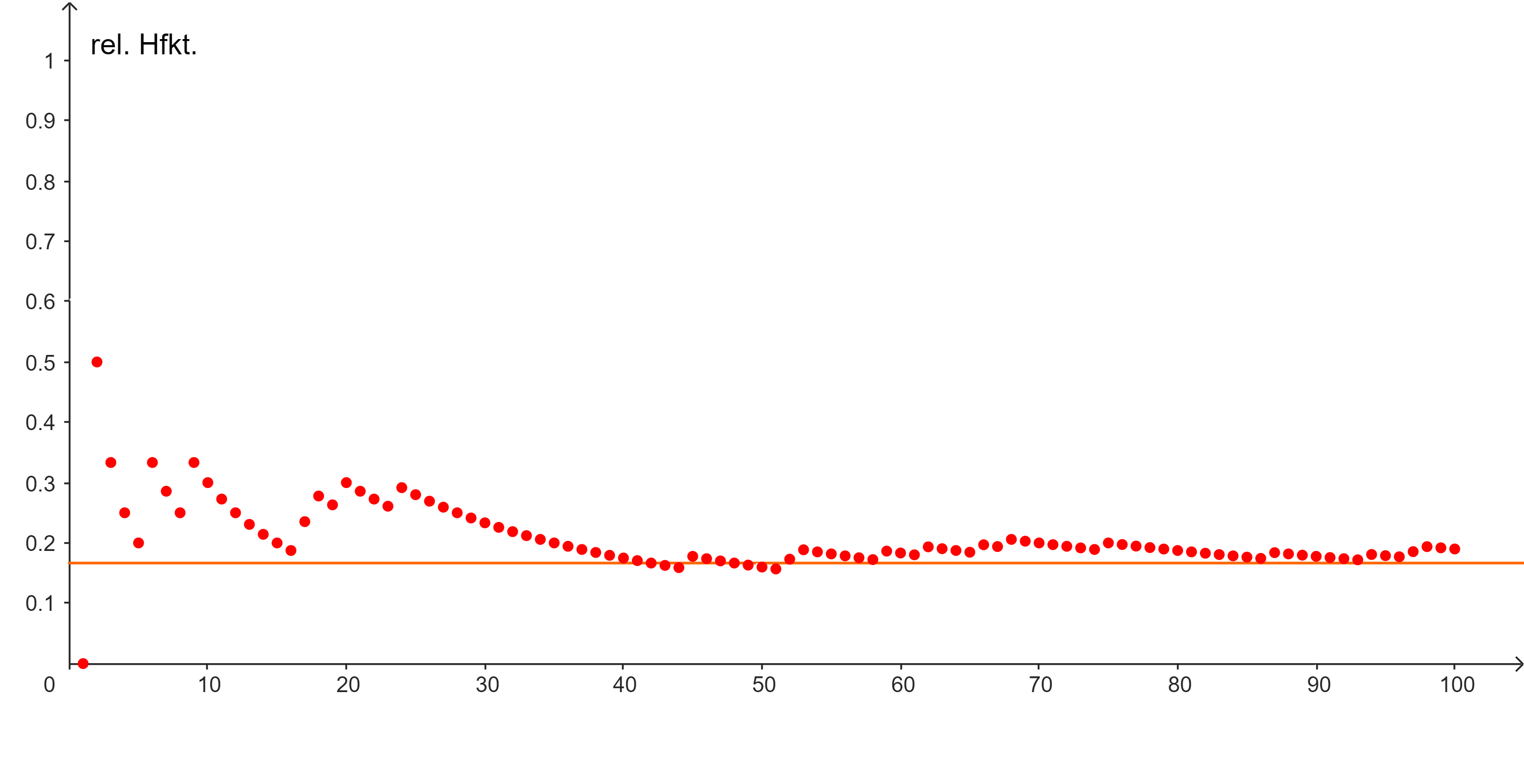
Auf der x-Achse kann die Anzahl der Wiederholungen abgelesen werden, auf der y-Achse die zugehörigen relativen Häufigkeiten des Ergebnisses „Augenzahl 1“.
Für eine kleine Anzahl von Wiederholungen schwanken die relativen Häufigkeiten noch stark. Mit zunehmender Anzahl von Wiederholungen nehmen die Schwankungen immer mehr ab, wodurch ein (mehr oder weniger) stabiler Endwert gefunden wird. Dieser Stabilisierungseffekt kann auch noch präziser gefasst werden, indem die Schwankungen mit Schranken beschrieben werden. Das werden wir in einem der weiteren Kapitel genauer betrachten.
Empirisches Gesetz der großen Zahlen
Wenn ein Zufallsexperiment wiederholt durchgeführt wird, dann stabilisieren sich mit zunehmender Wiederholungszahl die relativen Häufigkeiten der Ergebnisse.
Das Stabilisierungsverhalten bei der wiederholten Durchführung von Zufallsexperimenten ermöglicht es, das Eintreffen von Ergebnissen bei Zufallsexperimenten mit Hilfe von Zahlen - die wir Wahrscheinlichkeiten nennen - zu beschreiben.
Wahrscheinlichkeiten als Prognosewerte für relative Häufigkeiten
Bei einem fairen Standardwürfel wird davon ausgegangen, dass alle Augenzahlen mit den gleichen Chancen fallen und auf lange Sicht somit etwa gleich oft auftreten. Wir beschreiben diese Annahme, indem wir jeder Augenzahl die Wahrscheinlichkeit $\frac{1}{6}$ zuordnen.
| Augenzahl $e$ | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ |
|---|---|---|---|---|---|---|
| Wahrscheinlichkeit $P(e)$ | $\frac{1}{6}$ | $\frac{1}{6}$ | $\frac{1}{6}$ | $\frac{1}{6}$ | $\frac{1}{6}$ | $\frac{1}{6}$ |
Die Zahl $\frac{1}{6}$ für das Ergebnis „Augenzahl 6“ wird folgendermaßen gedeutet: Wenn ein Standardwürfel oft (z.B. 1000-mal) geworfen wird, dann wird erwartet, dass das Ergebnis „Augenzahl 6“ in etwa mit dieser relativen Häufigkeit in der Würfelserie vorkommt. Bei 1000 Würfen bedeutet dies, dass die 6 etwa $\frac{1}{6} \cdot 1000 = 167$ mal fällt.
Wahrscheinlichkeiten als Prognosewerte für relative Häufigkeiten
Angenommen, wir kennen die Wahrscheinlichkeit eines Ergebnisses. Dann benutzen wir diese Wahrscheinlichkeit als Prognosewert für die relative Häufigkeit bei einer geplanten Versuchsreihe.
Bei der Deutung und Verwendung von Wahrscheinlichkeiten ist der Blick also immer ein vorausschauender.
Relative Häufigkeiten als Schätzwerte für Wahrscheinlichkeiten
Häufig ist es so, dass die Wahrscheinlichkeiten der Ergebnisse eines Zufallsexperiments nicht bekannt sind. In diesem Fall werden experimentell bestimmte relative Häufigkeiten von langen Versuchsreihen als bestmögliche Schätzwerte für die (nicht bekannten) Wahrscheinlichkeiten genutzt. Betrachte als Beispiel einen Pyramidenwürfel, bei dem mehrere Würfelserien mit jeweils 500 Würfelwürfen durchgeführt wurden. Die Tabelle zeigt die jeweils ermittelten relativen Häufigkeiten der Augenzahlen:
| Augenzahl e | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ |
|---|---|---|---|---|---|---|
| relative Häufigkeit $h(e)$ [Version 1] | $0.358$ | $0.158$ | $0.146$ | $0.138$ | $0.138$ | $0.062$ |
| relative Häufigkeit $h(e)$ [Version 2] | $0.318$ | $0.13$ | $0.136$ | $0.17$ | $0.192$ | $0.054$ |
| relative Häufigkeit $h(e)$ [Version 3] | $0.372$ | $0.138$ | $0.156$ | $0.148$ | $0.1442$ | $0.042$ |
Ausgehend von diesen empirisch ermittelten Daten (sowie der Annahme, dass bei einem symmetrischen Pyramidenwürfel die „Seitenzahlen“ 2, 3, 4, 5 auf lange Sicht wohl gleich oft fallen werden) könnten die Wahrscheinlichkeiten der Augenzahlen so festgelegt werden:
| Augenzahl $e$ | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ |
|---|---|---|---|---|---|---|
| geschätzte Wahrscheinlichkeit $P(e)$ | $0.35$ | $0.15$ | $0.15$ | $0.15$ | $0.15$ | $0.05$ |
Beachte, dass die Wahrscheinlichkeiten hier gesetzt werden. Es ist nicht möglich, Wahrscheinlichkeiten mit Hilfe von Versuchsreihen exakt zu bestimmen. Auf diese Schwierigkeit gehen wir im nächsten Kapitel nochmal genauer ein.
Relative Häufigkeiten als Schätzwerte für Wahrscheinlichkeiten
Angenommen, wir kennen die relative Häufigkeit eines Ergebnisses aus einer oft wiederholten Durchführung des Zufallsexperiments. Dann benutzen wir die relative Häufigkeit als Schätzwert für die Wahrscheinlichkeit des Ergebnisses.
Die Bestimmung von Wahrscheinlichkeiten mit Hilfe von relativen Häufigkeiten erfolgt somit rückblickend auf bereits vorliegende Daten.

