Überprüfung - Ereignisse

Aufgabe 1

Beim Roulette wird eine kleine Kugel in den Roulette-Kessel geworfen, die nach mehreren Runden im Kessel zufällig auf einer der 37 Zahlen von 0 bis 36 liegen bleibt. Die Zahlen sind in 18 rote und 18 schwarze Zahlen sowie die grüne Null eingeteilt.

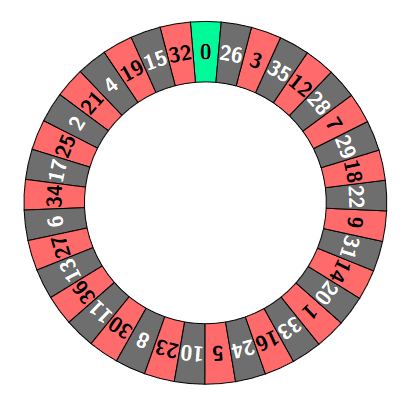
Benutze zur Beschreibung der Ausgangssituation beim Roulette das folgende Wahrscheinlichkeitsmodell:

Realität	Modell
Zufallsexperiment: eine Kugel in den Roulette-Kessel werfen und dabei die Zahl beobachten, auf der die Kugel liegen bleibt.
Ergebnisse: Zahlen 0, ..., 36	Ergebnismenge: { 0, 1, 2, ..., 36 }
Wahrscheinlichkeitsannahme: Alle Ergebnisse sind gleich wahrscheinlich.	Wahrscheinlichkeitsfunktion: $P(e) = \displaystyle{\frac{1}{37}}$ für alle Ergebnisse $e$ aus $\Omega$

Für das Wetten werden Chips auf ein Roulette-Tableau gesetzt.

Beim Wetten spielen Ereignisse eine zentrale Rolle. Zeige anhand der folgenden Beispiele, wie Ereignisse mathematisch beschrieben werden und wie die zugehörigen Wahrscheinlichkeiten bestimmt werden.

• $A$: "Rouge" bzw. die Kugel fällt auf eine rote Zahl
• $B$: "Cheval" bzw. die Kugel fällt auf zwei benachbarte Zahlen auf dem Tableau (wie z. B. 0 und 2)
• $C$: "Milieu" bzw. die Kugel fällt auf die mittleren Zahlen 13-24

Aufgabe 2 - Daten einer Erhebung

In einer Studie wurde die Nutzung von Social Media in den verschiedenen Altersgruppen untersucht (siehe Studie). In dieser Studie wurden u. a. folgende Daten erhoben:

Gehe von den Daten in der folgenden Übersicht aus:

	Babyboomer	Generation X	Generation Y	Generation Z	Summe
ja	18	41	62	36	...
nein	344	250	209	64	...
Summe	...	...	...	...	...

Betrachte die Befragung als Zufallsexperiment: "eine (beliebig ausgewählte) Person befragen und dabei die Antworten auf die beiden Merkmale Altergruppe und Social-Media-Nutzung beobachten".

Zur Beschreibung der Befragungsresultate benutzen wir die folgenden Ereignisse:

• $B$: Altersgruppe? Babyboomer
• $X$: Altersgruppe? Generation X
• $Y$: Altersgruppe? Generation Y
• $Z$: Altersgruppe? Generation Z
• $J$: Social-Media-Nutzung mehr als 10-mal am Tag? ja

Ergänze die Einträge in der Tabelle.

Ereignis	Beschreibung	Wahrscheinlichkeit
$\overlinepatch{J}$	Die befragte Person ...	$P(\overlinepatch{J}) = \displaystyle{\frac{867}{1004} \approx \dots}$
$X \cup Y$	...	...
$B \cap J$	...	...
$\overlinepatch{B} \cap \overlinepatch{J}$	...	...
$Z \cap \overlinepatch{J}$	...	...
$(X \cup Y \cup Z) \cap J$	...	...