Erkundung - Abstände im Kristallgitter

Kristalle untersuchen

Kristalle sind Körper, deren Bausteine (Atome oder Moleküle) gitterförmig angeodnet sind. Das Foto zeigt eine Nahaufnahme von Kochsalz (NaCl), das eine kristalline Struktur hat.

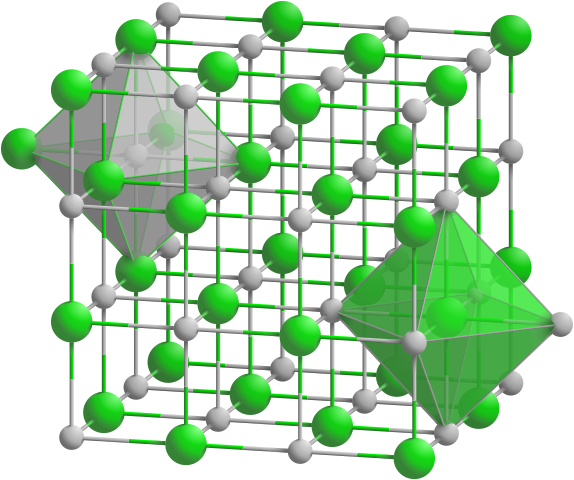
Die Anordnung der Kochsalzatome basiert auf einem einfachen kubischen Gitter (grau: Na⁺-Ionen; grün: Cl^--Ionen).

In solchen Kristallgittern interessiert man sich häufig für die Abstände von Gitterpunkten. Mit solchen Abstandsbestimmungen werden wir uns hier beschäftigen.

Abstände mit Hilfe von Vektoren bestimmen

Zum Herunterladen: betrag1.ggb

Aufgabe 1

(a) Erläutere, was man unter dem Betrag $|\vec{v}|$ eines Vektors $\vec{v}$ versteht.

(b) Erkläre, wie man mit Hilfe des Satzes von Pythagoras zur Formel $|\vec{v}| = \sqrt {v_1^2 + v_2^2 + v_3^2}$ gelangt.

(c) Verdeutliche am Beispiel, wie man den Abstand $d(P, Q)$ zwischen zwei Punkten $P$ und $Q$ mit dem Betrag eines geeigneten Vektors bestimmen kann. Erkläre das Vorgehen anhand der Formel $d(P, Q) = | \overrightarrow{ PQ } |$.

Abstände im Kristallgitter bestimmen

Wir betrachten ein einfaches kubisches Kristallgitter, bei dem die Gitterpunkte würfelartig angeordnet sind. Wir gehen dabei davon aus, dass die Würfel die Kantenlänge 1 haben. Das Applet zeigt einen Ausschnitt aus einem solchen Kristallgitter.

Zum Herunterladen: gitter1.ggb

Aufgabe 2

(a) Betrachte den Punkt $P$, der im Koordinatenursprung liegen soll. Begründe, dass $P$ im Gitter von insgesamt 26 direkten Nachbarn umgeben wird. Bestimme die Abstände zu diesen Nachbarn. Du musst keine 26 Rechnungen durchführen – manche Abstände sind aus Symmetriegründen gleich.

(b) Erkläre, welche Abstände zu direkten Nachbarn im vorgegebenen Gitter möglich sind. Erstelle eine Skizze, in der mit unterschiedlichen Farben die Gitterpunkte mit jeweils gleichem Abstand markiert sind.