Beschränktheit von Folgen
Begriffe definieren
In diesem Abschnitt klären wir Begriffe, die man zur Beschreibung der Beschränktheit von Folgen benutzt.
| Eigenschaft | Bedingung | Beispiel |
|---|---|---|
| es gibt eine reelle Zahl | 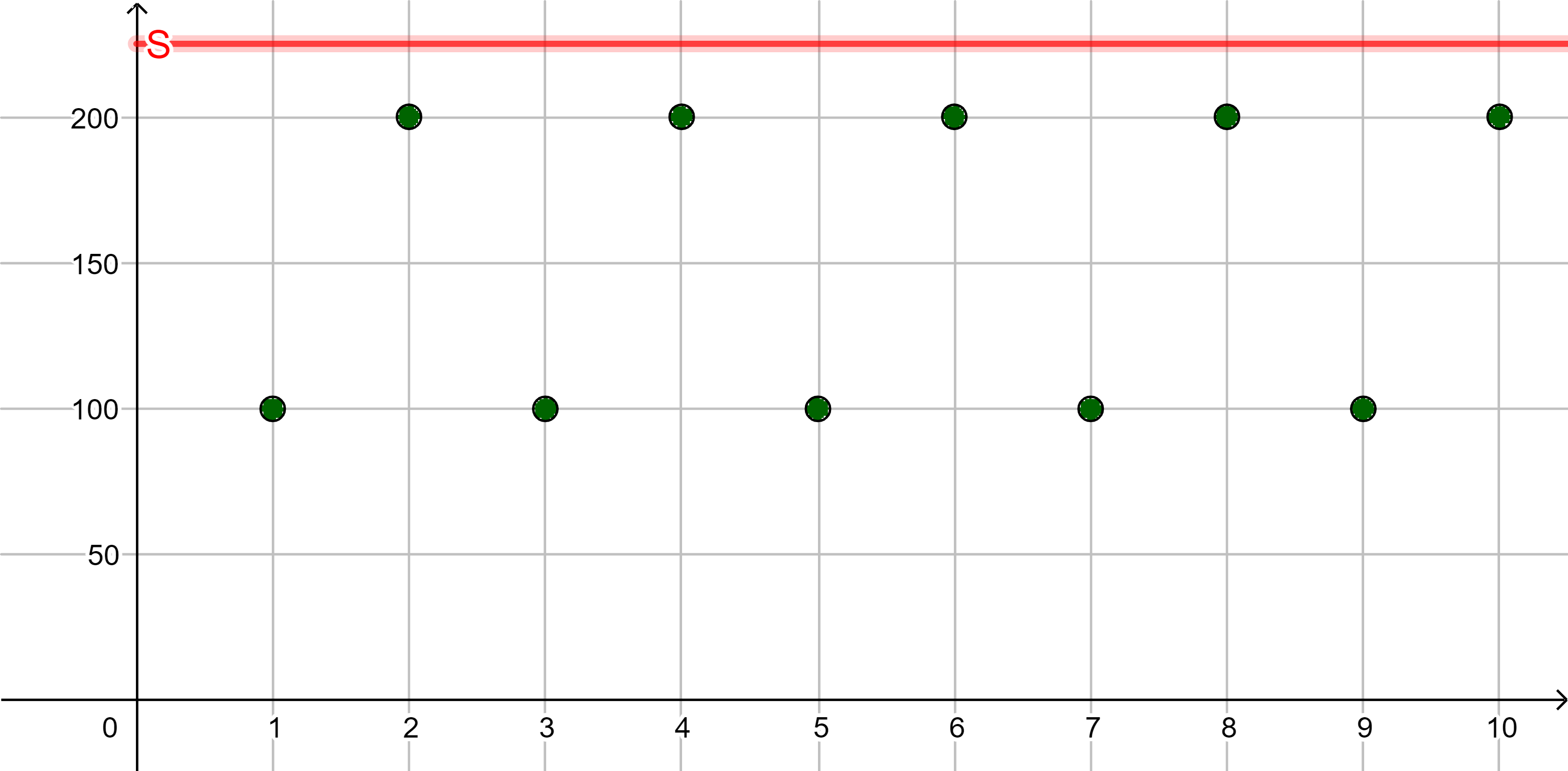 | |
| es gibt eine reelle Zahl | 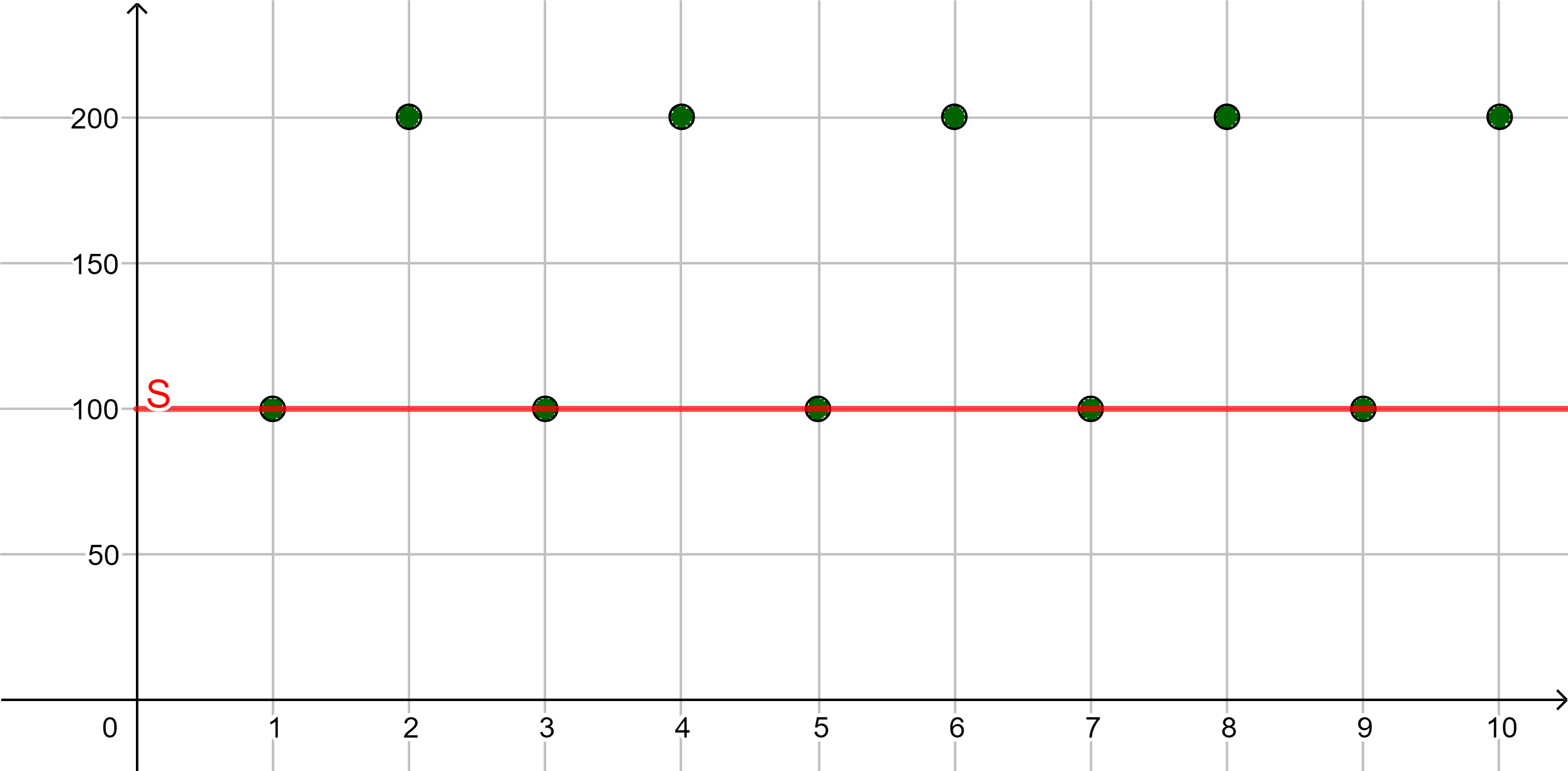 | |
Aufgabe 1
(a) Beschreibe in eigenen Worten, was die oben definierten Begriffe bedeuten.
(b) Skizziere eine Folge, die nicht nach oben beschränkt ist.
(c) Stimmt das: Wenn eine Folge eine obere (bzw. untere) Schranke hat, dann hat sie unendlich viele obere (bzw. untere) Schranken.
Aufgabe 2
Halte deine Ergebnisse in diesem Wissensspeicher fest.

