Anzahl der Züge
Die minimale Anzahl der Bewegungen bestimmen
Wir betrachten das Umschichtungsproblem jetzt aus einer anderen Perspektive.
Gegeben ist ein Turm mit $n$ Scheiben im Stapel A. Gesucht ist die minimale Anzahl $a_n$ von Scheibenbewegungen (bzw. Zügen), die man benötigt, um den Turm über den Hilfsstapel B zum Zielstapel C umzuschichten.
Zustand vorher:
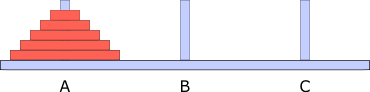
Zustand nachher:
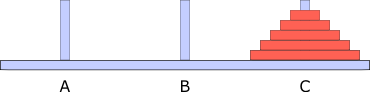
Aufgabe 1
(a) Beginne mit den einfachsten Fällen. Bestimme $a_1$ und $a_2$. Diese Werte kann man sofort angeben.
(b) Bestimme anschließend $a_3$. Dazu musst du wissen, wie man einen 3-Scheiben-Turm umschichtet.
(c) Bestimme auch $a_4$. Nutze die im letzten Abschnitt entwickelte Strategie zur Lösung des Umschichtungsproblems.
Eine Zahlenfolge beim Problemlösen nutzen
Wenn man die minimalen Anzahlen von Bewegungen $a_1; a_2; a_3; a_4; a_5; ...$ zum Umschichten eines $n$-Scheiben-Turmes systematisch bestimmt, dann ergibt sich diese Zahlenfolge:
$1; 3; 7; 15; 31; ...$
Aufgabe 2
(a) Vielleicht ist dir auch schon folgende Gesetzmäßigkeit aufgefallen:
$a_2 = 2 \cdot a_1 + 1$
$a_3 = 2 \cdot a_2 + 1$
$a_4 = 2 \cdot a_3 + 1$
...
Erkläre, warum das so ist. Benutze das rekursive Löseverfahren, das im letzten Abschnitt entwickelt wurde.
(b) Beschreibe die Gesetzmäßigkeit jetzt allgemein. Ergänze hierzu die Formel für $a_n$.
$a_1 = 1$
$a_2 = 2 \cdot a_1 + 1$
$a_3 = 2 \cdot a_2 + 1$
$a_4 = 2 \cdot a_3 + 1$
...
$a_n = ...$ (für $n = 2, 3, ...$)
