Rekursive Darstellung einer Folge
Ein Knobelproblem mit einer Folge bearbeiten
Wir betrachten das Kartenhausproblem.
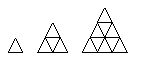
Für das 1. Kartenhaus benötigt man 3 Karten, für das 2. Kartenhaus 9 Karten. Das erhält man direkt durch Abzählen. Wie viele Karten benötigt man für das 10. bzw. 100. Kartenhaus?
Zur Bearbeitung des Problems benutzen wir eine Folge. Die Folge
Aufgabe 1
Ergänze die Formel für
...
Aufgabe 2
(a) Rekursive Darstellungen führen zu zurücklaufenden Berechnungen. Erkläre das Vorgehen bei der Ausführung einer Berechnung an folgendem Beispiel.
| rekursiver Abstieg | rekursiver Aufstieg |
|---|---|
(b) Begründe, warum eine rekursive Berechnung eines Folgenglieds recht aufwendig ist.
Aufgabe 3
Welche rekursive Darstellung kann man zur Berechnung der oben beschriebenen Folge nutzen? Begründe kurz.
Variante 1:
Variante 2:
Variante 3:
Aufgabe 4
(a) Es ist recht schwierig, eine explizite Formel für
Überprüfe, ob die Formel stimmt. Berechne hierzu zur Kontrolle mindestens 3 Folgenglieder.
(b) Mache dir an Beispiel "Kartenhaus" nochmal klar, dass es manchmel recht leicht ist, eine rekursive Darstellung einer Folge zu bestimmen. Die Berechnung der Folgenglieder ist dagegen aufwendig.

