Zusammenfassung - Beschränktheit von Folgen
Schranken für die Folgenglieder
Beschränktheitsbegriffe benutzt man, um Folgen zu beschreiben, deren Folgenglieder bestimmte Schranken nicht über- bzw. unterschreiten. In diesem Abschnitt werden diese Begriffe präzisiert und anhand von Beispielen verdeutlicht.
Nach oben beschränkte Folgen
Eine Folge $\left( a_n \right)$ heißt nach oben beschränkt genau dann, wenn es eine reelle Zahl $S$ ("d.h., eine obere Schranke") gibt, so dass für alle Folgenglieder die Bedingung $a_n \leq S$ erfüllt ist.
Beispiele:
| Folge | Eigenschaft |
|---|---|
 |
$a_1 \leq S$; $a_2 \leq S$; $a_3 \leq S$; ... |
 |
$a_1 \leq S$; $a_2 \leq S$; $a_3 \leq S$; ... |
 |
$a_1 \leq S$; $a_2 \leq S$; $a_3 \leq S$; ... |
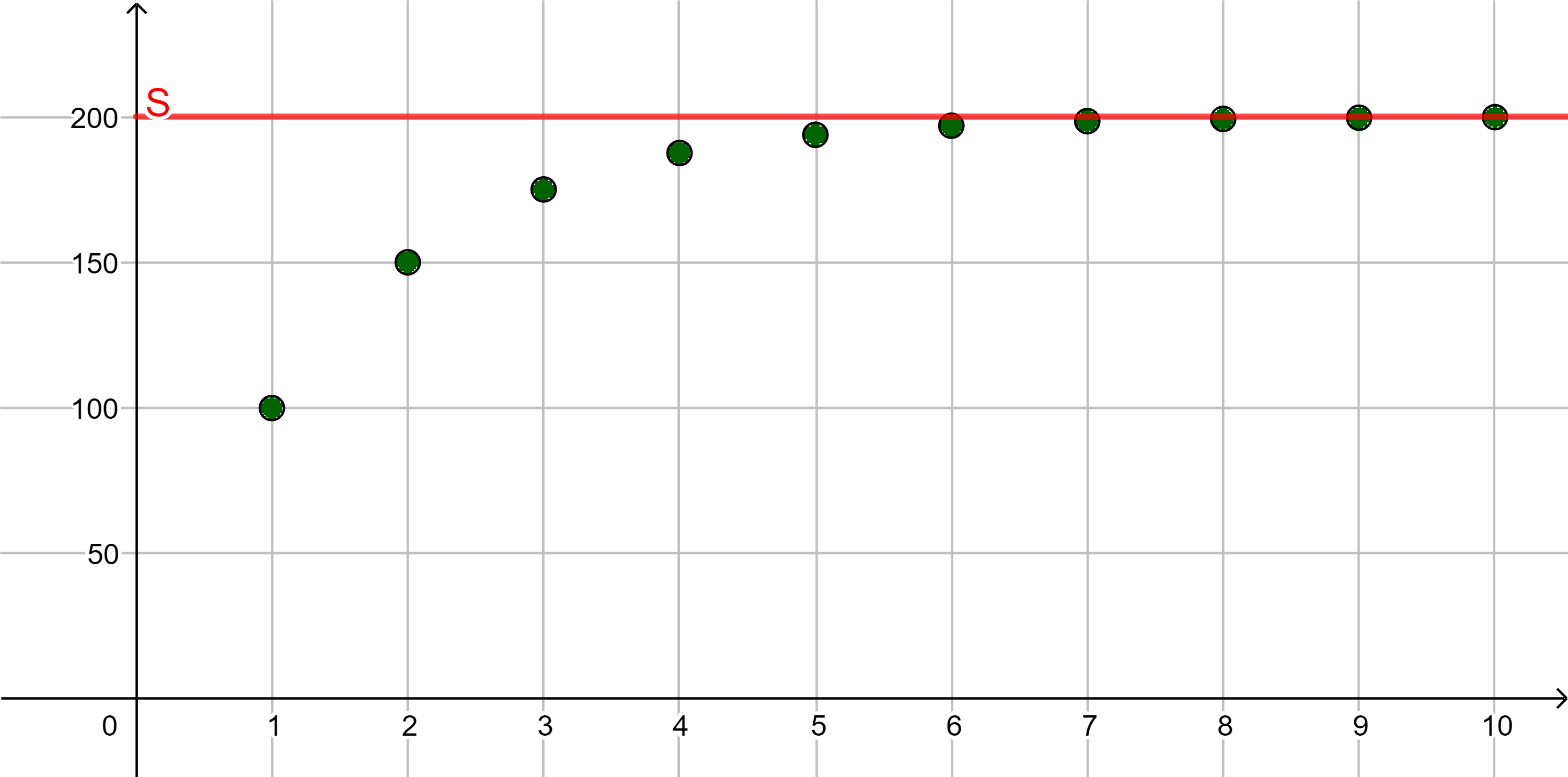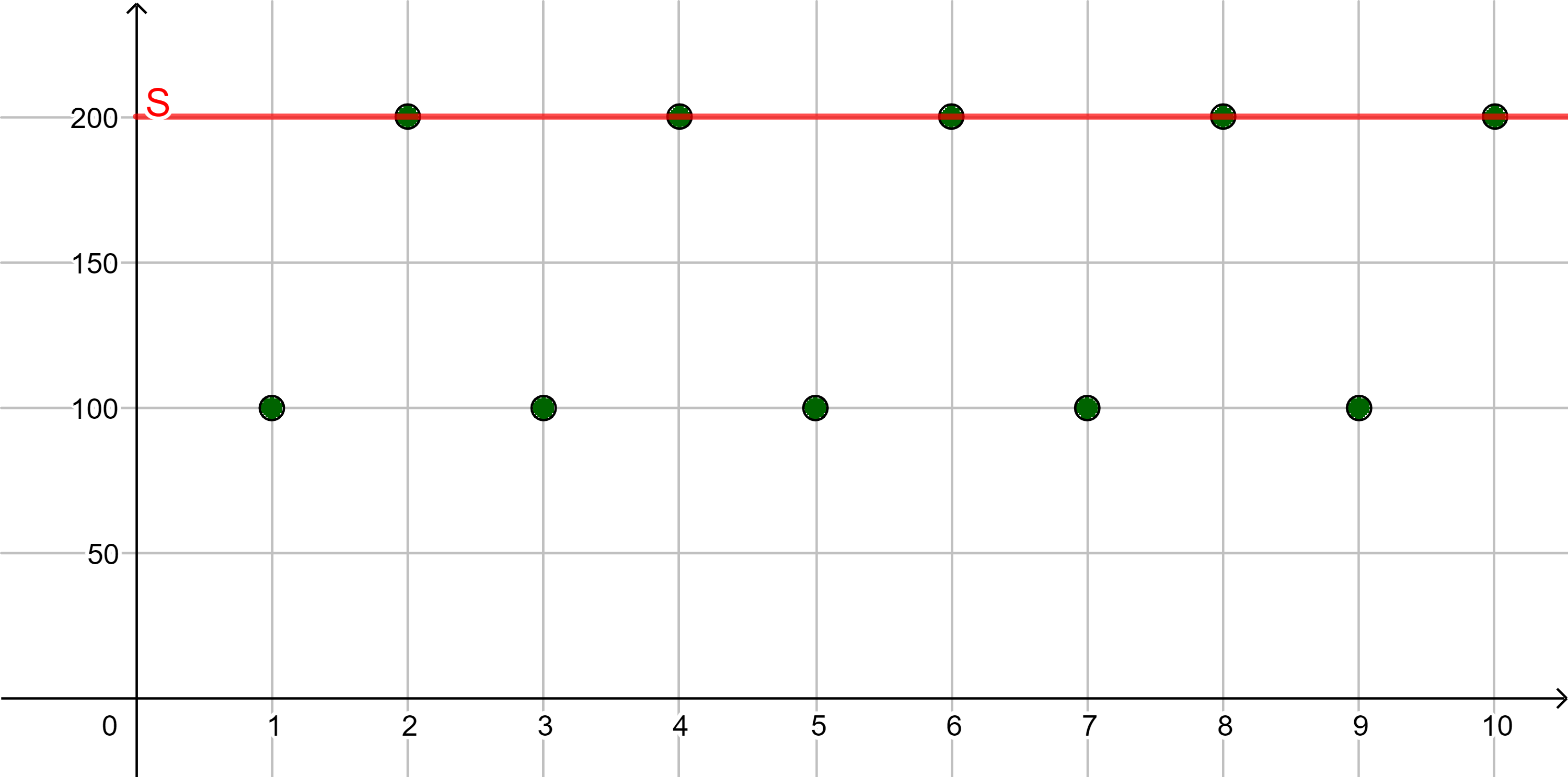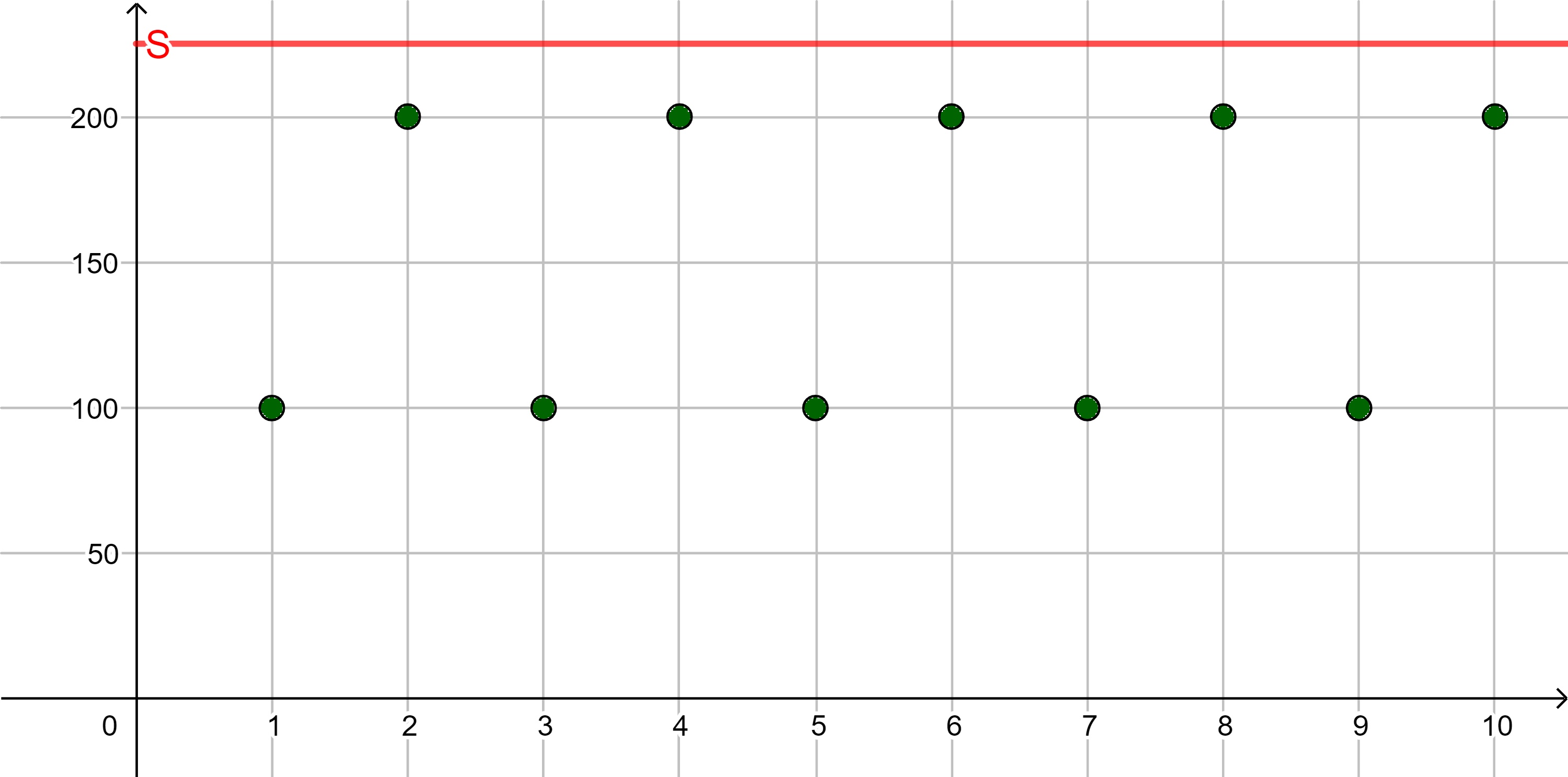Beachte: Wenn eine Folge nach oben beschränkt ist, dann hat sie unendlich viele obere Schranken. Das ist hier am 2. und 3. Beispiel verdeutlicht.
Nach unten beschränkte Folgen
Eine Folge $\left( a_n \right)$ heißt nach unten beschränkt genau dann, wenn es eine reelle Zahl $S$ ("d.h., eine untere Schranke") gibt, so dass für alle Folgenglieder die Bedingung $a_n \geq S$ erfüllt ist.
Beispiele:
| Folge | Eigenschaft |
|---|---|
 |
$a_1 \geq S$; $a_2 \geq S$; $a_3 \geq S$; ... |
 |
$a_1 \geq S$; $a_2 \geq S$; $a_3 \geq S$; ... |
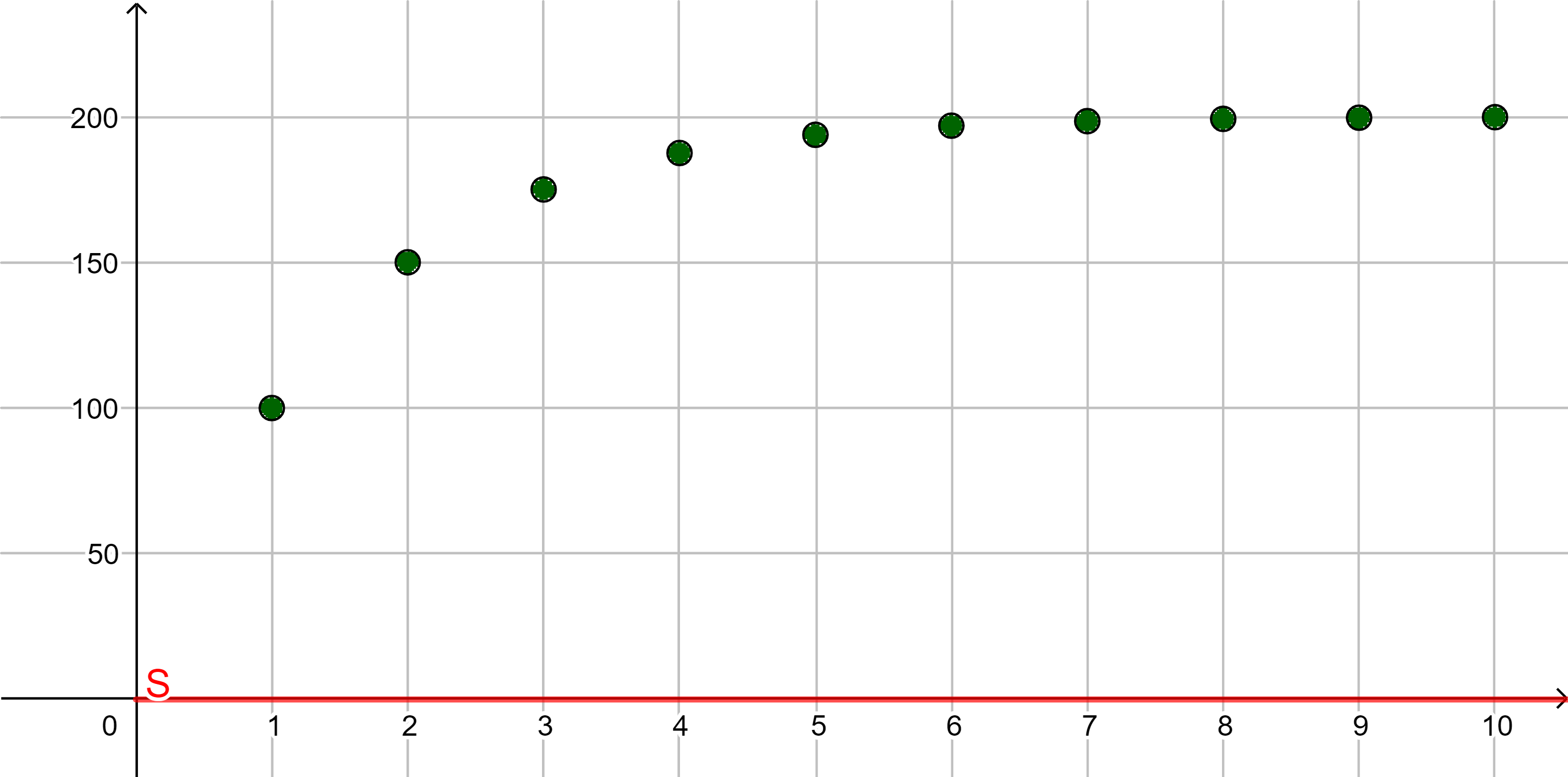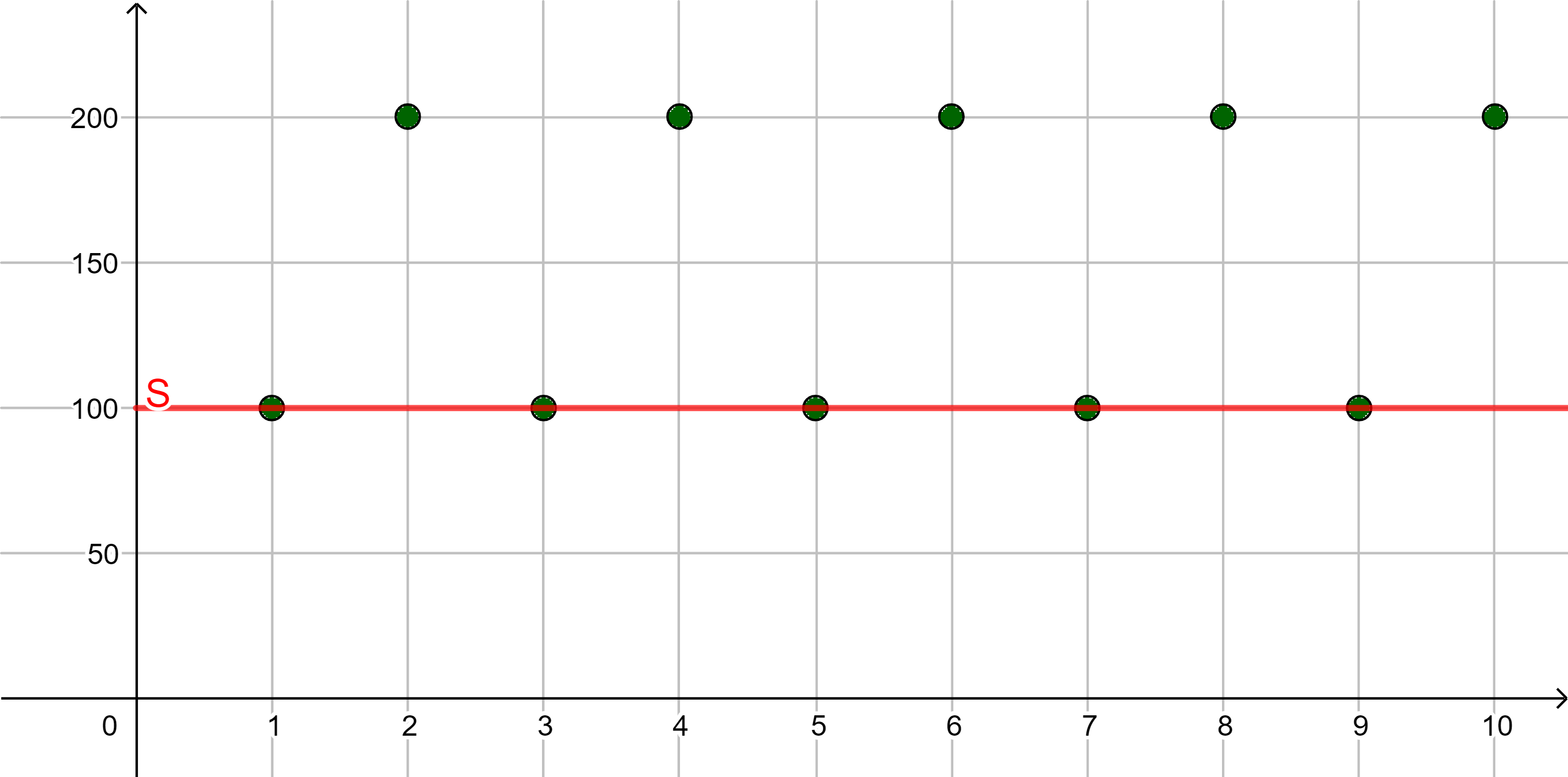Beachte: Wenn eine Folge nach unten beschränkt ist, dann hat sie unendlich viele untere Schranken.
Beschränkte Folgen
Eine Folge $\left( a_n \right)$ heißt beschränkt genau dann, wenn sie nach oben und unten beschränkt ist.
Beispiel:
| Folge | Eigenschaft |
|---|---|
 |
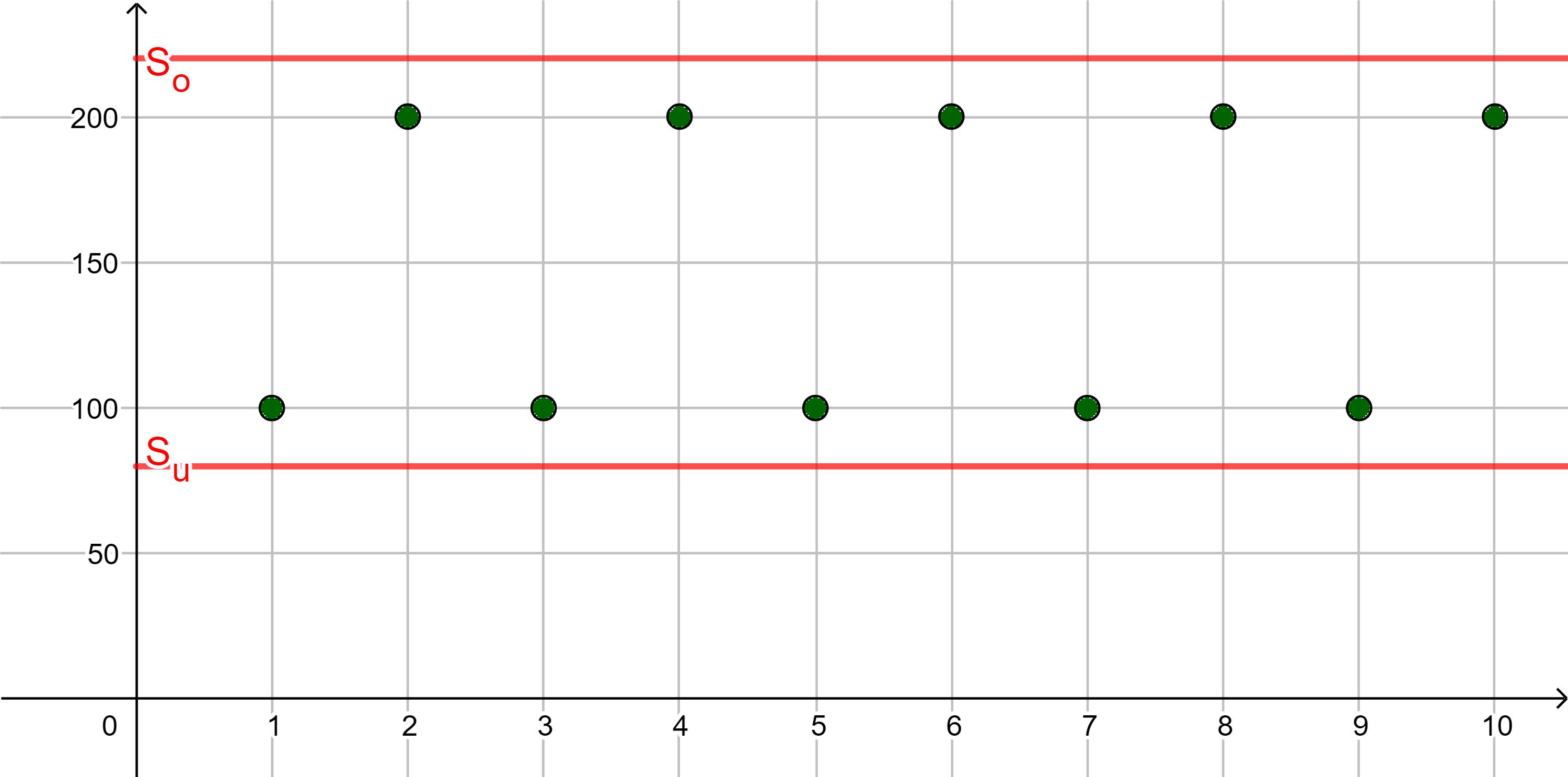$a_1 \geq S_u$; $a_2 \geq S_u$; ... $a_1 \leq S_o$; $a_2 \leq S_o$; ... |
