Monotonie von Folgen
Begriffe definieren
Begriffe müssen in der Mathematik klar und eindeutig festgelegt werden. Wir betrachten hier Begriffe zur Monotoniebeschreibung bei Folgen.
| Eigenschaft | Bedingung | Beispiel |
|---|---|---|
| für alle Folgenglieder gilt: |  | |
| für alle Folgenglieder gilt: | 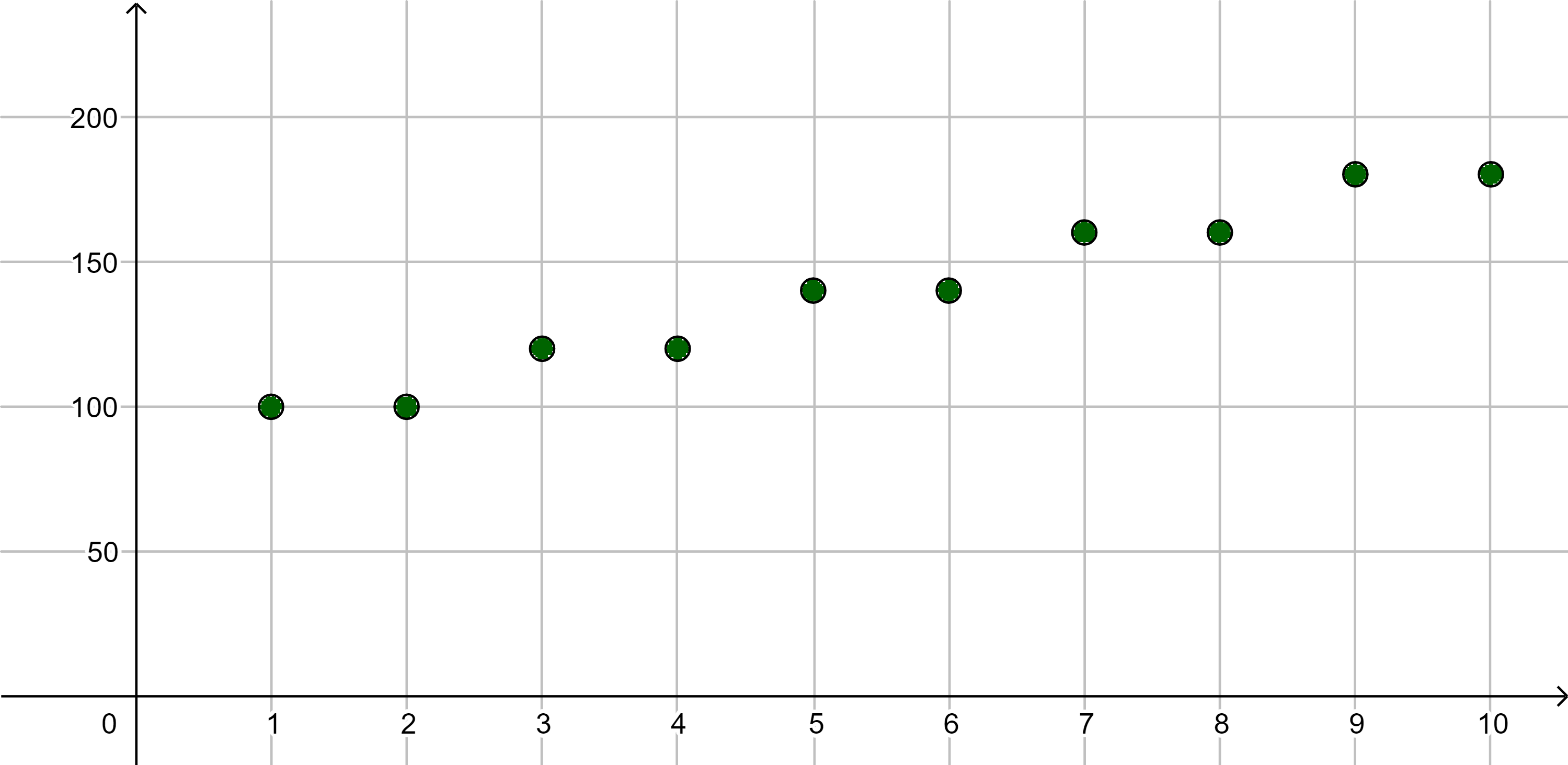 | |
| für alle Folgenglieder gilt: |  | |
| für alle Folgenglieder gilt: |  | |
Aufgabe 1
Ergänze in der Tabelle die fehlenden Bedingungen. Ergänze auch passende Beispiele.
Aufgabe 2
Ordne den Fachbegriffen die richtigen umgangssprachlichen Bedeutungsbeschreibungen zu.
- Die Folgenglieder werden mit zunehmender Platznummer nicht kleiner.
- Die Folgenglieder werden mit zunehmender Platznummer immer größer.
- Die Folgenglieder werden mit zunehmender Platznummer immer kleiner.
- Die Folgenglieder werden mit zunehmender Platznummer nicht größer.
Aufgabe 3
Halte deine Ergebnisse in diesem Wissensspeicher fest.
Aufgabe 4
Hier geht es um den Aufbau einer mathematischen Begriffsdefinition. Betrachte zunächst eine Begriffserläuterung aus dem Alltag: "Ein Hund wird bissig genannt, wenn er mehrfach Menschen gebissen hat."
(a) Welche Analogien gibt es zwischen einer mathematischen Begriffsdefinition und einer Begriffsklärung aus dem Alltag? Verdeutliche jeweils den zu definierenden Begriff und die dazu benutzte definierende Eigenschaft.
(b) Welche Unterschiede gibt es zwischen einer mathematischen Begriffsdefinition und einer Begriffsklärung aus dem Alltag? Gehe hier auf die Präzision und Verbindlichkeit ein.

