Vertiefung - Nachweis von Monotonie und Beschränktheit
Eigenschaften begründen
Die Begriffsdefinitionen zur Monotonie und Beschränktheit machen es möglich, Eigenschaften von Folgen argumentativ nachzuweisen. Wir nutzen hier inhaltliche Begründungen und verzichten auf strenge Beweise.
Beispiel 1
Als Beispiel betrachten wir die Folge $\left( a_n \right)$, die so festgelegt ist:
| Graph | Darstellung |
|---|---|
 |
$a_n = 200 \cdot (1 - 0.5^n)$ |
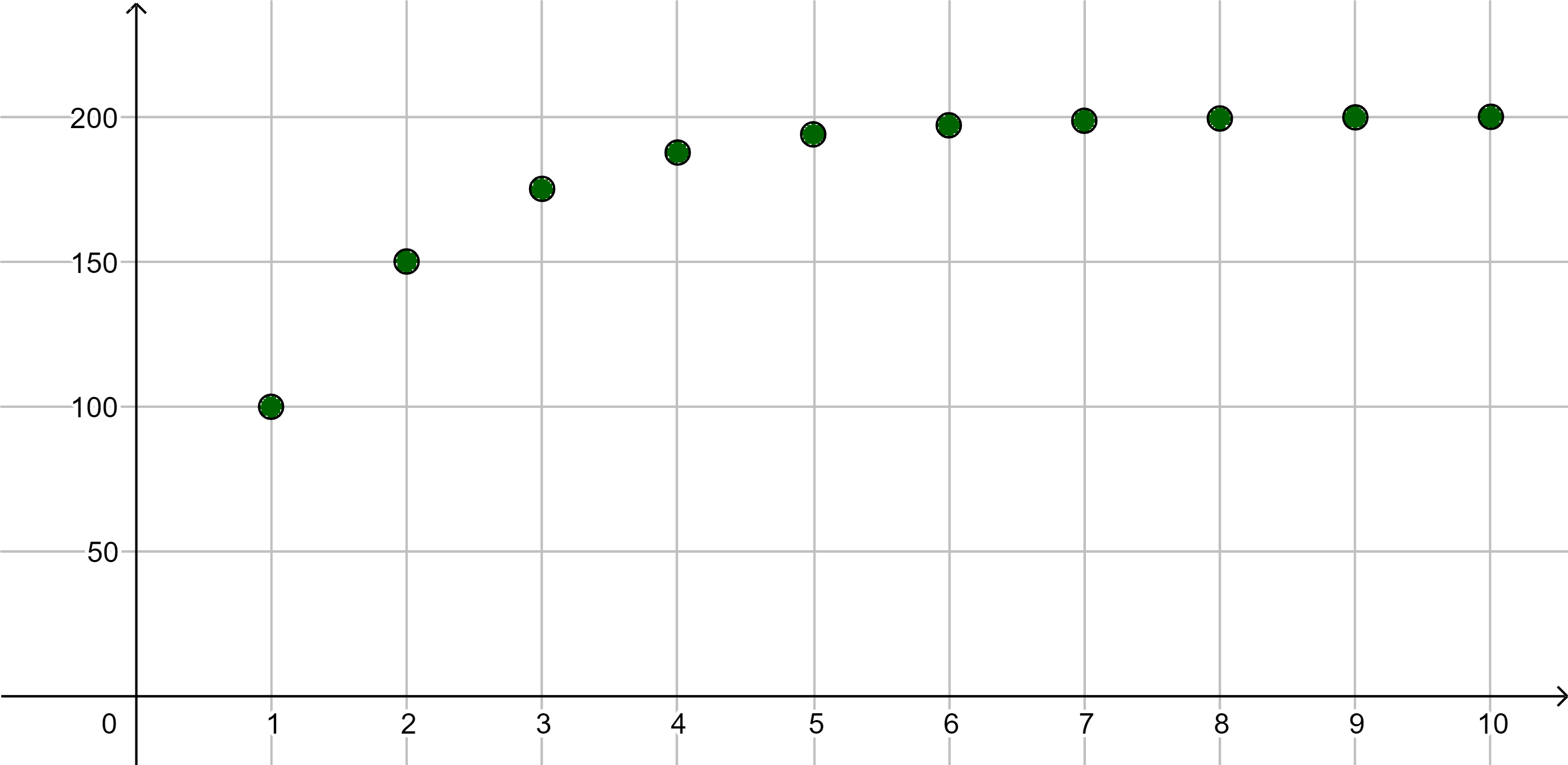Anhand des Graphen vermutet man, dass die Folge streng monoton steigend und nach oben und unten beschränkt ist.
Aufgabe 1: Beschränktheit begründen
(a) Begründe zunächst, dass $0 \text{ < } 0.5^n \text{ < } 1$ für $n = 1; 2; 3; ...$ gilt.
(b) Begründe mit Hilfe von (a), dass $a_n > 0$ und $a_n \text{ < } 200$ für alle Folgenglieder gilt.
(c) Welche Schranken ergeben sich hieraus für die Folge $\left( a_n \right)$? Formuliere entsprechende Beschränktheitsaussagen.
Aufgabe 2: Monotonie begründen
(a) Begründe zunächst, dass $0.5^n \text{ > } 0.5^{n+1}$ für $n = 1; 2; 3; ...$ gilt.
(b) Begründe mit Hilfe von (a), dass $a_n \text{ < } a_{n+1}$ für alle Folgenglieder gilt.
(c) Erläutere, welche Monotonieeigenschaft somit nachgewiesen ist.
Beispiel 2
Als Beispiel betrachten wir die Folge $\left( a_n \right)$, die so festgelegt ist:
| Graph | Darstellung |
|---|---|
 |
$a_n = 90 + 10\cdot n$ |
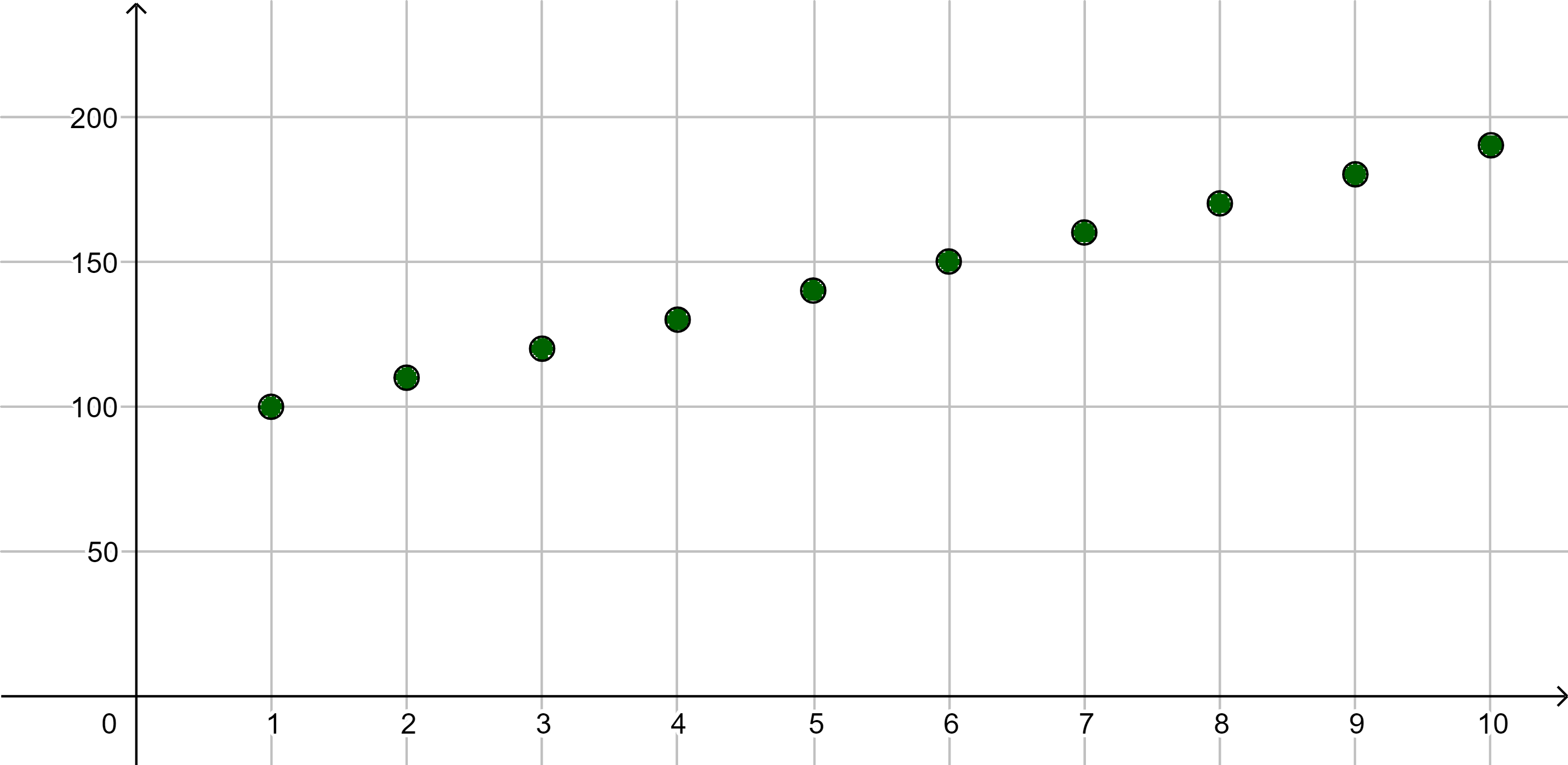Anhand des Graphen vermutet man, dass die Folge streng monoton steigend und nicht nach oben beschränkt ist.
Aufgabe 3: Monotonie begründen
(a) Begründe zunächst, dass $10 \cdot n \text{ < } 10 \cdot (n+1)$ für $n = 1; 2; 3; ...$ gilt.
(b) Begründe mit Hilfe von (a), dass $a_n \text{ < } a_{n+1}$ für alle Folgenglieder gilt.
(c) Erläutere, welche Monotonieeigenschaft somit nachgewiesen ist.
Aufgabe 4: Beschränktheit untersuchen
Kann es eine obere Schranke $S$ für die Folgenglieder geben?
(a) Kann $S = 1000$ eine obere Schranke für die Folgenglieder sein? Begründe, dass man eine Platznummer $n$ findet, so dass $a_n > S$ gilt.
(b) Begründe, dass man für beliebige Werte für $S$ eine Platznummer $n$ findet, so dass $a_n > S$ gilt.
(c) Erläutere, welche Schlüsse man aus (b) hinsichtlich der Beschränktheit der Folge ziehen kann.
