Lösungsidee

Große und kleine Probleme

Dir ist sicherlich aufgefallen, dass es einfach ist, einen kleinen Turm umzuschichten. Je größer der Turm wird, desto länger dauert es und desto schwieriger ist es auch, die richtige Abfolge an Zügen zu finden. Es hilft deshalb, erst kleine Türme zu betrachten und nach einem Muster zu suchen, wie man mit der Lösung für einen kleinen Turm auch einen größeren Turm umschichten kann.

Das kleine Problem lösen

Wir beginnen damit, 2er- und 3er-Türme zu verschieben. Das Vorgehen schreiben wir dabei sehr ausführlich auf. Das wirkt auf den ersten Blick unnötig aufwändig, wird uns aber für größere Türme weiterhelfen.

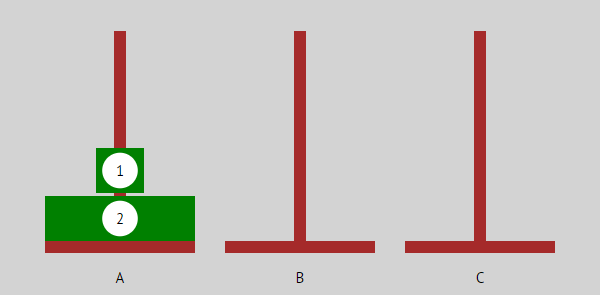	Startzustand: Alle Scheiben liegen auf einem Turm.
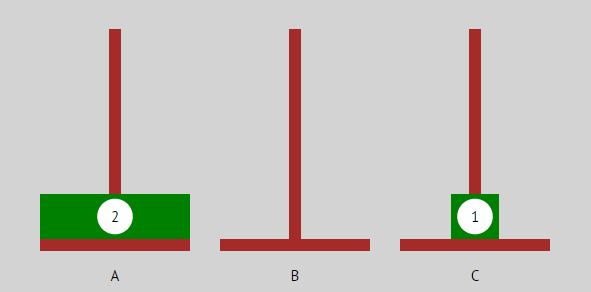	Erst wird die oberste Scheibe (das ist ein 1-Scheiben-Turm) verschoben. Jetzt ist die unterste Scheibe „frei“. Das braucht einen Zug.
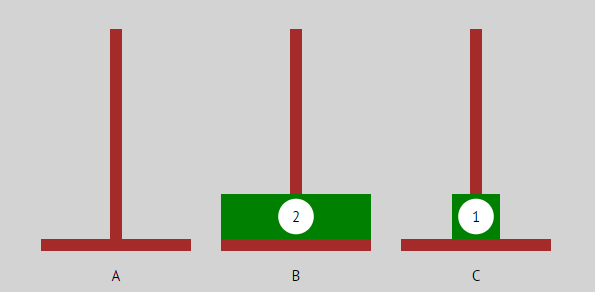	Jetzt wird die unterste Scheibe verschoben. Das braucht einen Zug.
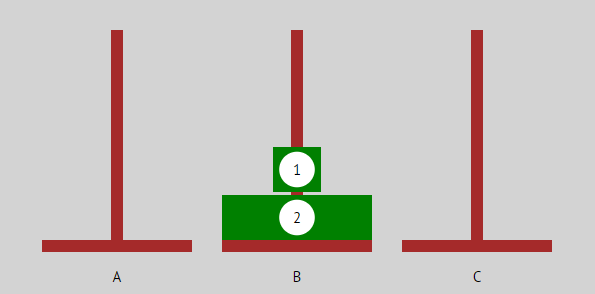	Jetzt wird der 1-Scheiben-Turm auf die verschobene unterste Scheibe verschoben. Das braucht einen Zug.

Aufgabe 1

Vollziehe diese Beschreibung nach. Beantworte: Wie viele Züge braucht man für einen 2er-Turm?

Aufgabe 2

Vervollständige genau wie oben die nachfolgende Beschreibung für einen 3er-Turm.

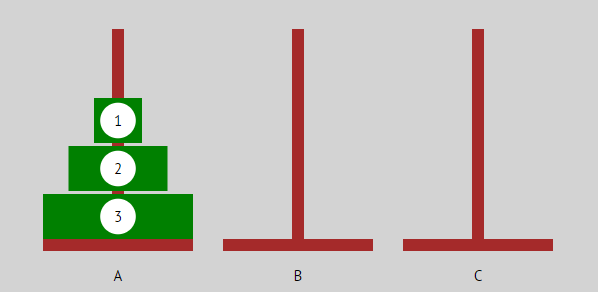	Startzustand: Alle Scheiben liegen auf einem Turm.
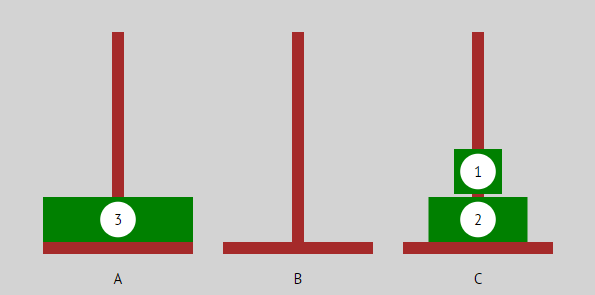	Erst wird ein 2-Scheiben-Turm verschoben. Jetzt ist die unterste Scheibe „frei“. Das braucht 3 Züge.
	...
	...

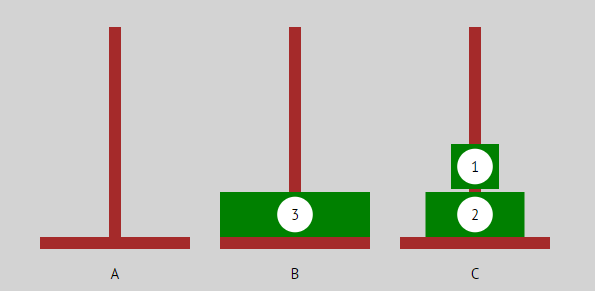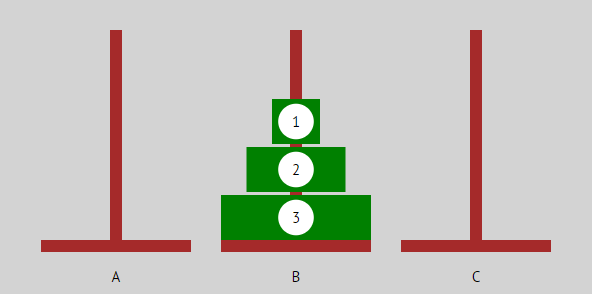Größere Probleme lösen

Wir gehen davon aus, dass wir auf dieselbe Weise Beschreibungen für einen 4-Scheiben-Turm, einen 5-Scheiben-Turm, usw. bis zum 9-Scheiben-Turm erstellt haben.

Aufgabe 3

Erstelle in der gleichen Art und Weise eine Beschreibung für einen 10-Scheiben-Turm (inklusive Skizzen). Mache dir noch keine Gedanken darüber, wie viele Züge es wohl dauern wird.

Das allgemeine Problem lösen

Du hast sicherlich bemerkt: Wenn man das 9-Scheiben-Problem gelöst hat, dann kann man auch einen 10-Scheiben-Turm umschichten. Dieser Zusammenhang kann auch allgemein formuliert werden. Dazu nutzt man dann eine Variable $n$ für die Anzahl der Scheiben.

Aufgabe 4

Formuliere eine allgemeine Anleitung, um einen $n$-Scheiben-Turm zu verschieben.

Hilfe