Zusammenfassung - Monotonie von Folgen
Steigende und fallende Folgen
Monotoniebegriffe benutzt man, um steigende bzw. fallende Folgen zu beschreiben. In diesem Abschnitt werden diese Begriffe präzisiert und anhand von Beispielen verdeutlicht.
Streng monoton steigende bzw. streng monoton fallende Folgen
Eine Folge $\left( a_n \right)$ heißt streng monoton steigend genau dann, wenn für alle Folgenglieder die Bedingung $a_n \text{ < } a_{n+1}$ erfüllt ist.
Beispiele:
| Folge | Eigenschaft |
|---|---|
 |
$a_1 \text{ < } a_2 \text{ < } a_3 \text{ < } ...$ |
 |
$a_1 \text{ < } a_2 \text{ < } a_3 \text{ < } ...$ |
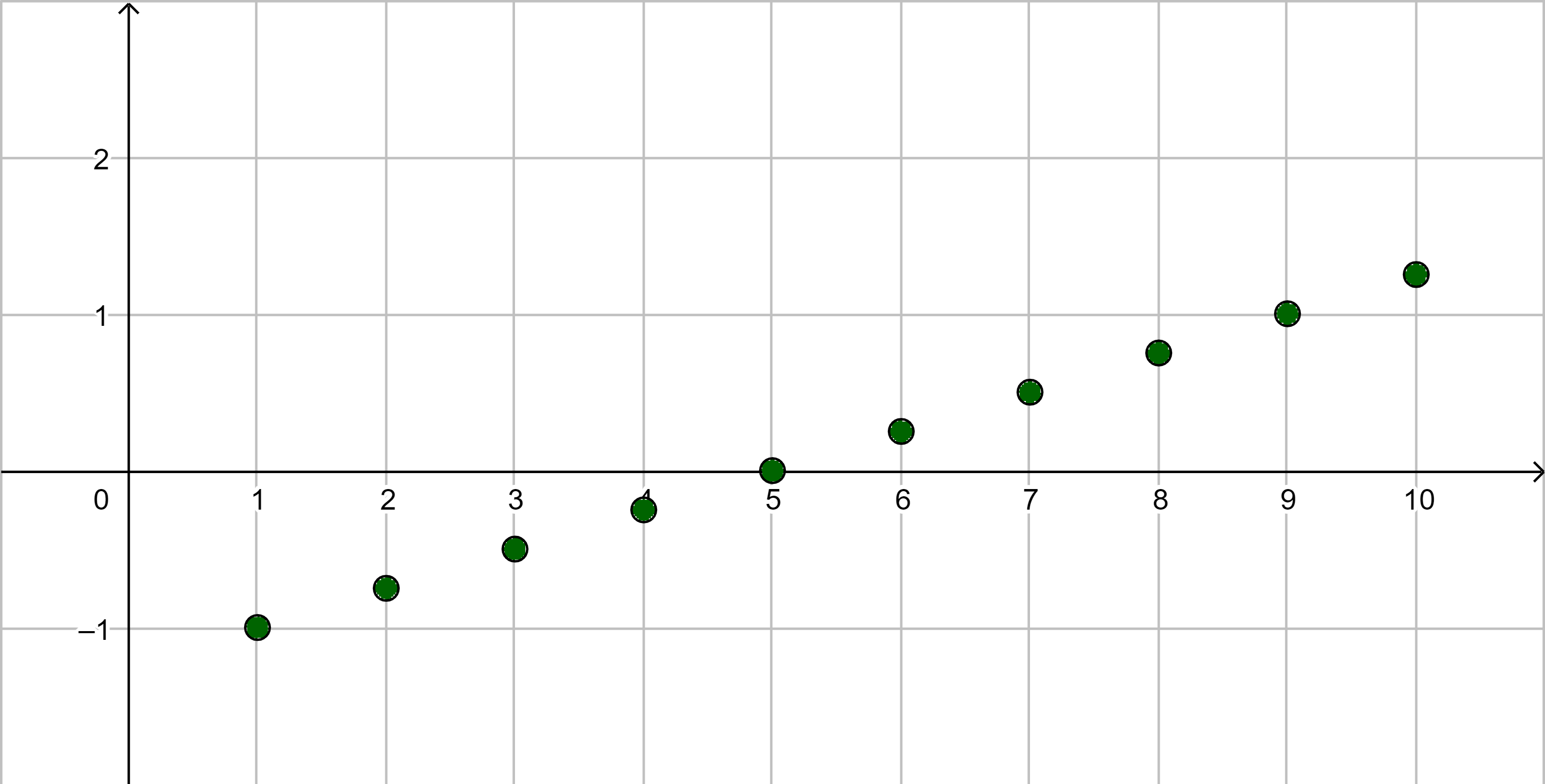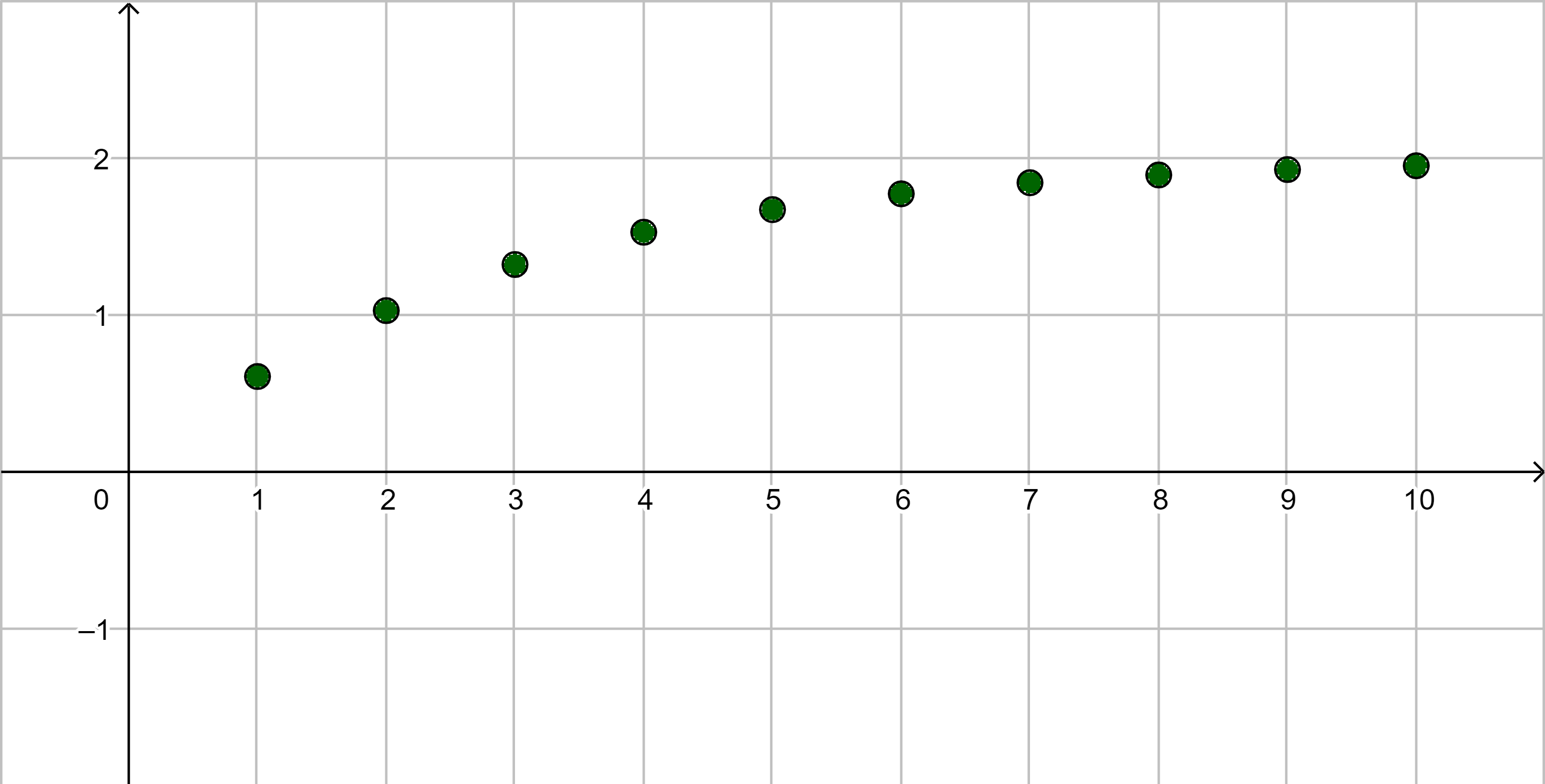Eine Folge $\left( a_n \right)$ heißt streng monoton fallend genau dann, wenn für alle Folgenglieder die Bedingung $a_n > a_{n+1}$ erfüllt ist.
Beispiele:
| Folge | Eigenschaft |
|---|---|
 |
$a_1 > a_2 > a_3 > ...$ |
 |
$a_1 > a_2 > a_3 > ...$ |
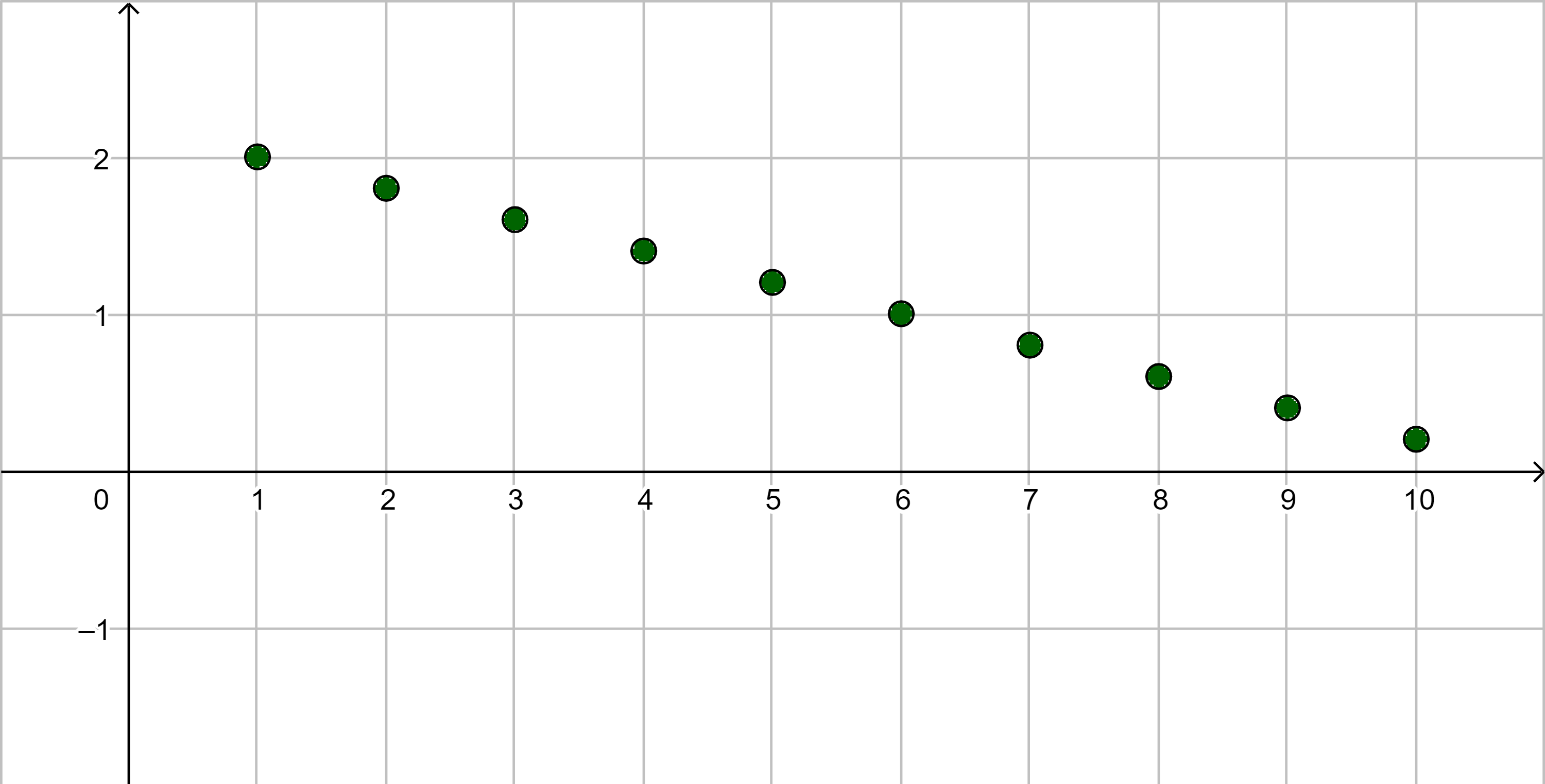Monoton steigende bzw. monoton fallende Folgen
Diese Begriffe beschreiben eine weniger strenge Form von Steigen und Fallen. Aufeinanderfolgende Folgenglieder können auch gleich sein.
Eine Folge $\left( a_n \right)$ heißt monoton steigend genau dann, wenn für alle Folgenglieder die Bedingung $a_n \leq a_{n+1}$ erfüllt ist.
Beispiele:
| Folge | Eigenschaft |
|---|---|
 |
$a_1 \leq a_2 \leq a_3 \leq ...$ |
|
$a_1 \leq a_2 \leq a_3 \leq ...$ |
 |
$a_1 \leq a_2 \leq a_3 \leq ...$ |
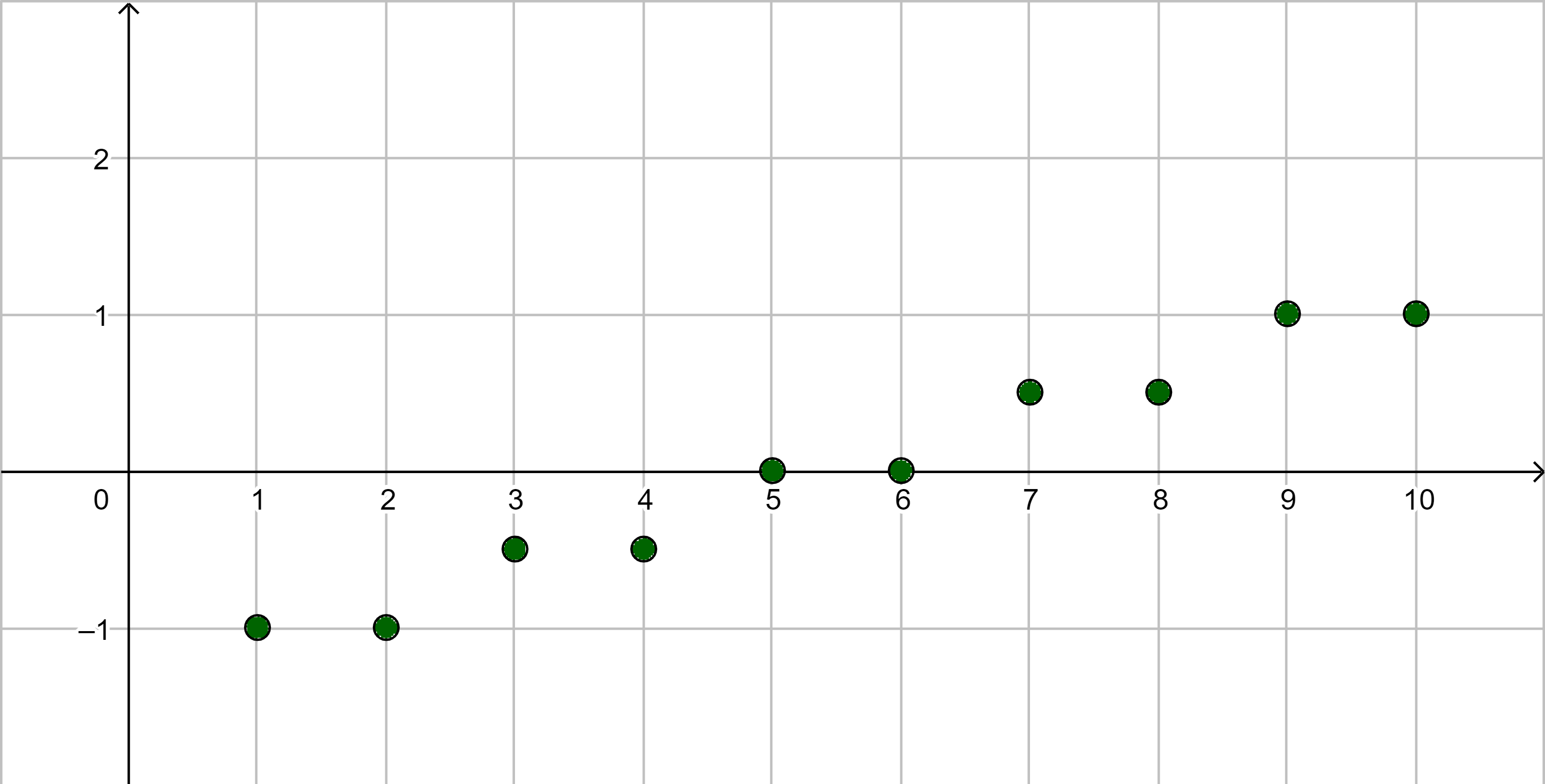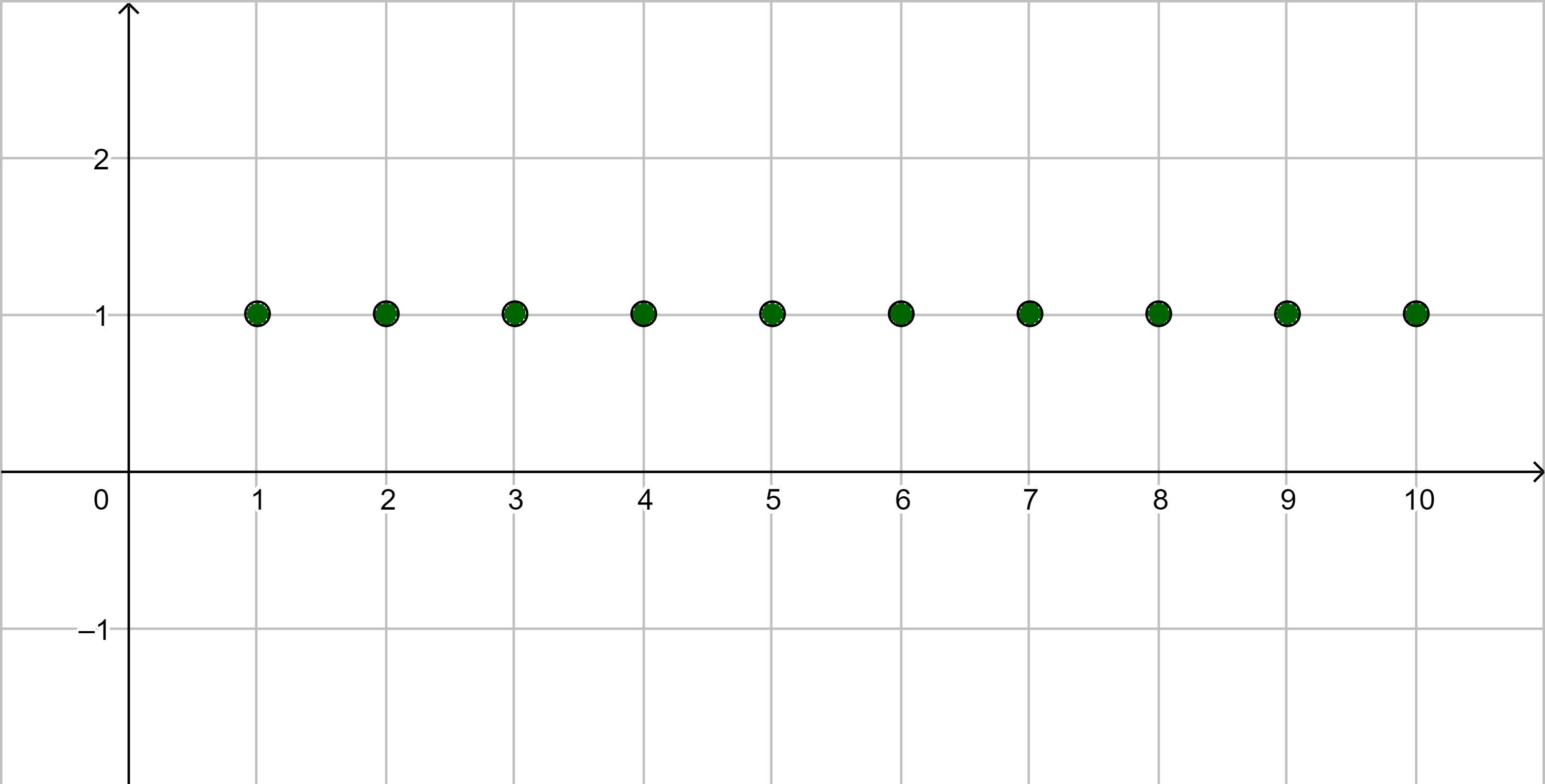Eine Folge $\left( a_n \right)$ heißt monoton fallend genau dann, wenn für alle Folgenglieder die Bedingung $a_n \geq a_{n+1}$ erfüllt ist.
Beispiele:
| Folge | Eigenschaft |
|---|---|
 |
$a_1 \geq a_2 \geq a_3 \geq ...$ |
|
$a_1 \geq a_2 \geq a_3 \geq ...$ |
|
$a_1 \geq a_2 \geq a_3 \geq ...$ |
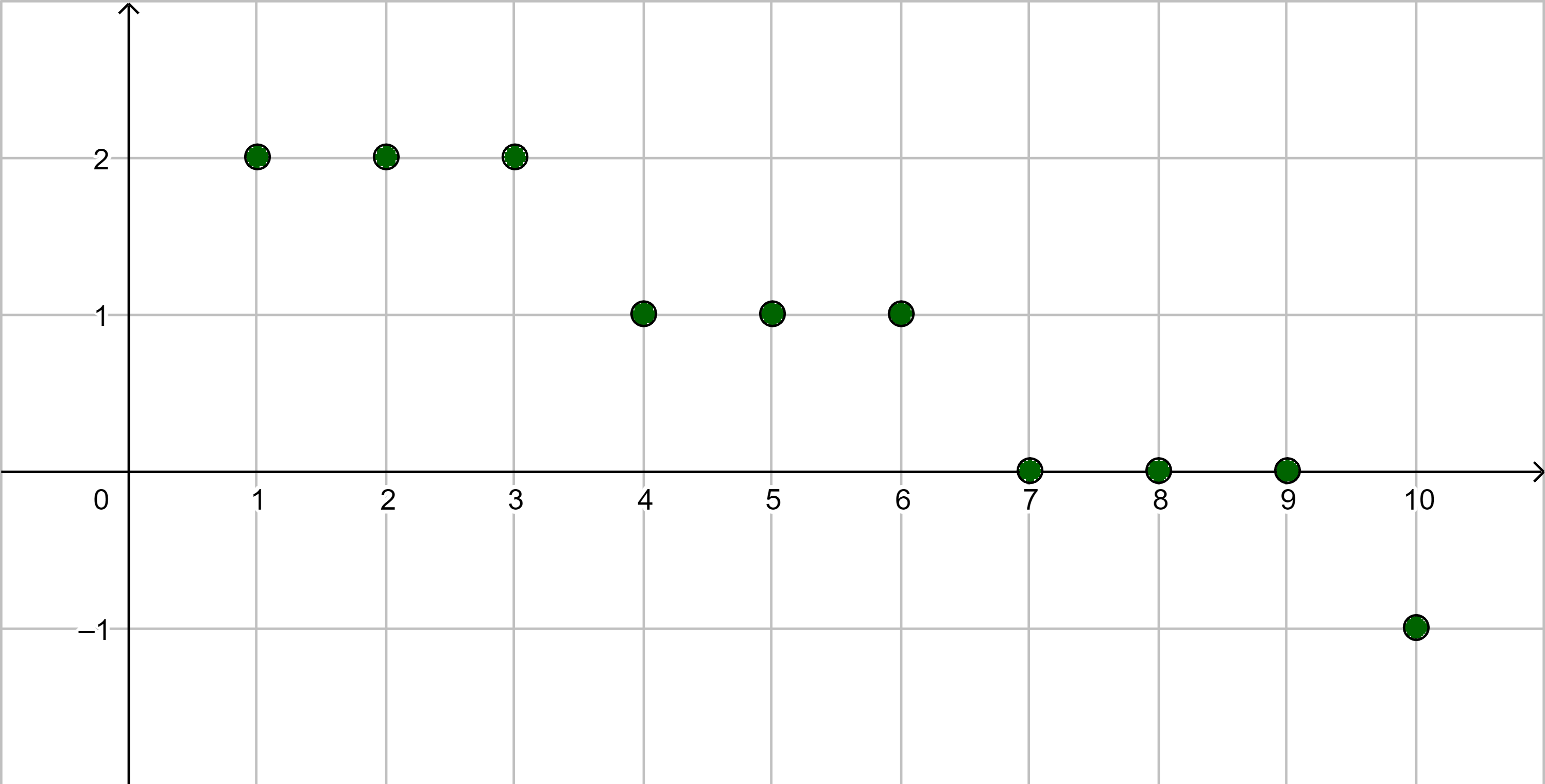Beachte die Sonderfälle:
- Wenn eine Folge streng monoton steigend (bzw. fallend) ist, dann ist sie auch monoton steigend (bzw. fallend).
- Eine Folge, bei der alle Folgenglieder gleich sind, ist monoton steigend und auch monoton fallend.
