Experimente
Eine Lösungsidee suchen
Hier kannst du experimentell Lösungsideen zum Umschichtungsproblem zu den Türmen von Hanoi entwickeln.
Gegeben ist ein Turm mit $n$ (z.B. $n = 5$) Scheiben im Stapel A. Schichte die Scheiben unter Berücksichtigung der Transportregeln so um, dass der Turm schließlich im Stapel C entsteht. Benutze B als Hilfsstapel.
Zustand vorher:
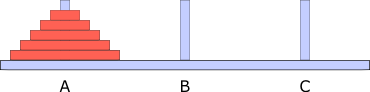
Zustand nachher:
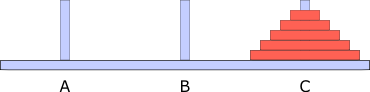
Aufgabe 1
(a) Beim Problemlösen ist es oft günstig, mit einfachen Fällen zu beginnen. Löse das Umschichtungsproblem zunächst für $n = 3$ Scheiben. Benutze das Applet unten.
(b) Erhöhe dann Schritt für Schritt die Anzahl der Scheiben. Tipp: Wenn man einen 4-Scheiben-Turm umschichten will, dann ist es günstig, wenn man weiß, wie man einen 3-Scheiben-Turm umschichtet.
(c) Formuliere eine Strategie, wie man beim Umschichten der Scheiben vorgehen sollte.
Aufgabe 2
Wenn du das Umschichten von Türmen beherrschst, dann beschäftige dich mit der Anzahl der benötigten Züge. Gesucht ist die minimale Anzahl von Zügen (das sind die Scheibentransporte), die man benötigt, um einen Turm mit 3 (bzw. 4, 5, 6, ...) Scheiben umzuschichten.
