Explizite Darstellung einer Folge
Ein Knobelproblem mit einer Folge bearbeiten
Wir betrachten das Streichholzlegeproblem.
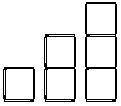
Wie viele Streichhölzer benötigt man für den 10. bzw. 100. Turm?
Zur Bearbeitung des Problems benutzen wir eine Folge. Die Folge
Aufgabe 1
(a) Ergänze die Formel für
...
(b) Benutze die Formel für
Aufgabe 2
Die Folge
...
Aufgabe 3
(a) Warum ist es günstiger, die in Aufgabe 1 ermittelte Formel zur Berechnung von
(b) In Aufgabe 1 wird eine explizite Darstellung der Folge entwickelt. Erläutere kurz, was der Begriff explizit hier bedeutet.

