Orientierte Flächeninhalte
Worum geht es hier?
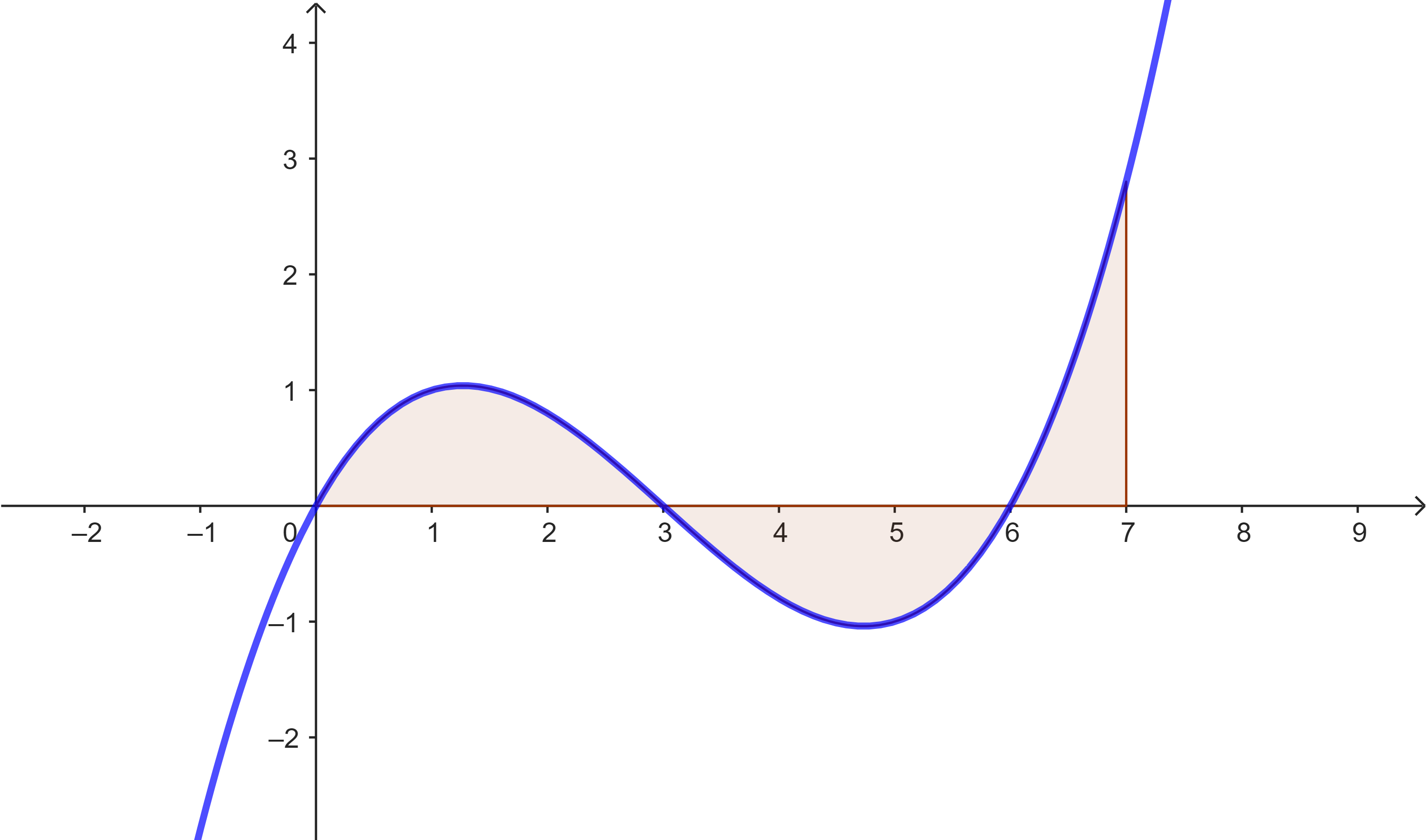
Das Integral wurde im letzten Unterkapitel als Grenzwert von Produktsummen eingeführt. Es lässt sich geometrisch als orientierter Flächeninhalt zwischen dem Graph der betrachteten Funktion und der x-Achse deuten.
Die exakte Bestimmung von Integralen über Grenzwerte von Produktsummen ist oft schwierig und aufwendig. Mit der Deutung des Integrals als orientierter Flächeninhalt eröffnet sich eine Möglichkeit, geometrische Überlegungen bei der Integralbestimmung zu nutzen. Genau diesen Weg werden wir in diesem Kapitel bestreiten.
Für dieses Thema musst du ...
- ... sicher mit Funktionen umgehen können.
- ... elementargeometrische Flächenberechnungen beherrschen.
Hier lernst du, ...
- ... wie Integrale in einfachen Fällen geometrisch berechnet werden.
Diese Inhalte findest du hier:
- Erkundung — Geometrische Deutung des Integrals
- Übungen — Integral und orientierte Flächeninhalte
- Überprüfung — Integral und orientierte Flächeninhalte
- Zusammenfassung — Integral und orientierte Flächeninhalte

