Vertiefung - ein Positionsproblem

Zur Orientierung

Ziel ist es hier ebenfalls, aus Tachodaten die zurückgelegte Wegstrecke zu rekonstruieren. Dabei wird zusätzlich die Fahrtrichtung berücksichtigt. Die Bewegung wird hierzu in einem Bezugssystem beschrieben.

Positionsbestimmung in einem Bezugssystem

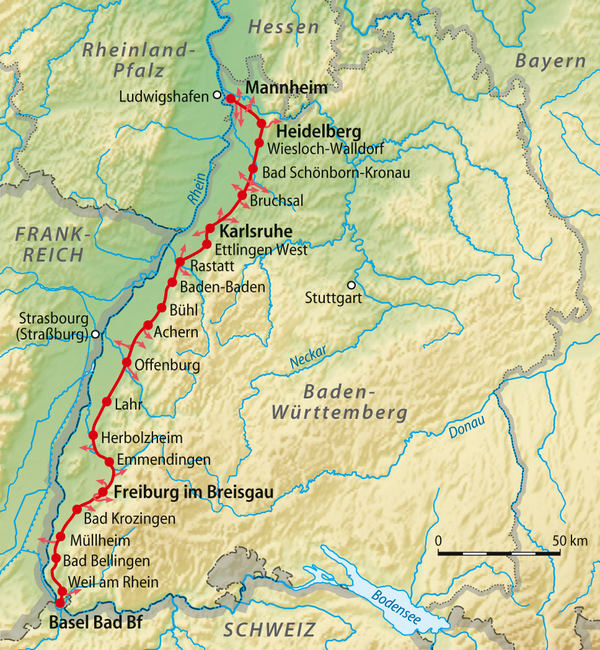
Wir betrachten im folgenden Bild die Bahnstrecke von Mannheim nach Basel:

Auf der Seite Bahnstrecke Mannheim–Basel ist eine Kilometrierung (als Kilometrierung bezeichnet man eine fortlaufende Meter- und Kilometer-Zählung entlang eines Verkehrsweges, bspw. eines Schienenweges) der Bahnstrecke dargestellt. In reduzierter und vereinfachter Form lässt sich die Kilometrierung der oben abgebildeten Bahnstrecke so darstellen:

Eine Kilometrierung bildet ein Bezugssystem, welches sich bei der Angabe von Positionen auf der Bahnstrecke nutzen lässt. Mit einem solchen Bezugssystem lassen sich auch Bahnfahrten exakt beschreiben.

Das folgende Applet stellt eine fiktive Bahnfahrt grob vereinfacht dar. Der Geschwindigkeitsverlauf der Bahnfahrt wird mit dem blauen Graphen der Funktion $v$ im unteren Fenster vorgegeben. Im oberen Fenster sollen die Positionen des Zugs aus dem Geschwindigkeitsverlauf rekonstruiert werden. Die aktuell zu sehenden Punkte sollen hierzu an passende Punkte verschoben werden. Bearbeite hierzu die nachfolgenden Aufgaben.

Zum Herunterladen: bahnfahrt.ggb

Aufgabe 1

(a) Beschreibe und erkläre diesen Geschwindigkeitsverlauf.

(b) Bestimme für die gegebenen Zeitpunkte die jeweilige Position des Zuges und verschiebe die Punkte des Graphens der Funktion $s$ passend. Kontrolliere anschließend deine Ergebnisse.

Zur Kontrolle

Zum Herunterladen: bahnfahrtKontrolle.ggb

(c) Vergleiche die Ergebnisse aus (b) mit der Beschreibung des Geschwindigkeitsverlaufs aus (a), indem du die Beschreibung präzisierst.

💡 Tipp

Nutze zur Beschreibung Formulierungen, wie: „Die Bahnfahrt startet bei/im Punkt .... Nach ... Stunden wird ... erreicht“.

(d) Stelle Zusammenhänge zwischen den Positionen im oberen Fenster und Flächen im unteren Fenster her und halte diese stichpunktartig fest.

💡 Tipp

Zum Herunterladen: bahnfahrtFlaechen.ggb

Aufgabe 2

🖊️ Wie bist du im obigen System zur Bestimmung der Ortspositionen vorgegangen? Beschreibe deine Strategie.

Rückblick

🖊️ Erläutere Zusammenhänge zwischen der Positionsbestimmung in Bezugssystemen und der Bestandsermittlung aus dem Kapitel Zufluss-Abfluss-System.