Integral und Flächeninhalte
Orientierte Flächeninhalte betrachten (Einstieg)
Im Kapitel Rekonstruktion eines Bestandes hast du gesehen, dass der Bestand aus einer Änderungsratenfunktion rekonstruiert werden kann, indem orientierte Flächeninhalte bestimmt werden.
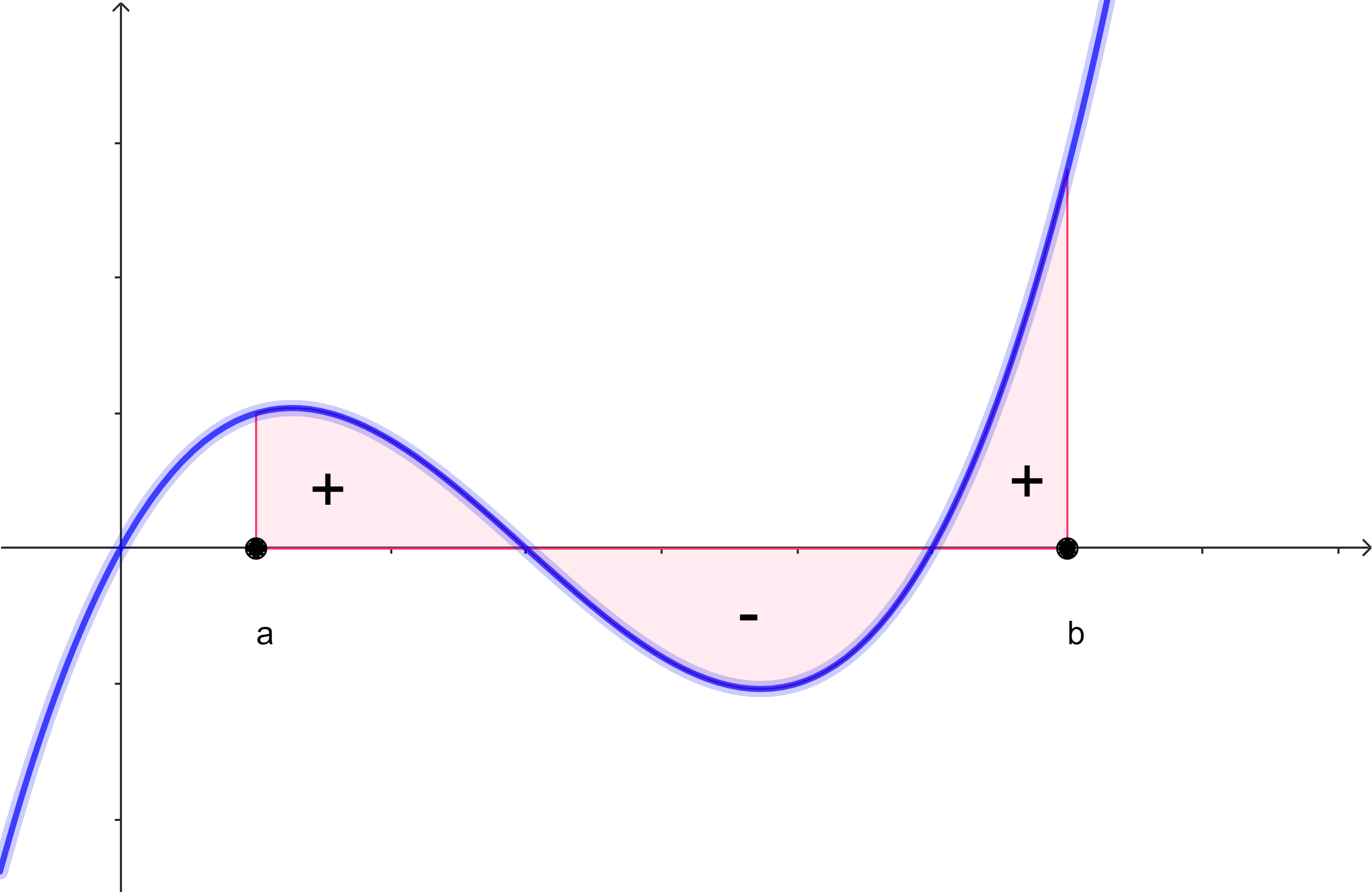
Der orientierte Flächeninhalt einer Funktion $f$ im Intervall $[a \, ; b]\in D$ ist die Summe der Flächeninhalte der Flächenstücke zwischen dem Graphen $G_f$ und der $x$-Achse im Intervall $[a \, ; b]$, in der die Flächenstücke oberhalb der $x$-Achse positive Summanden und Flächenstücke unterhalb der $x$-Achse negative Summanden sind.
Zusammenhang zum Integral (Einstieg)
Der orientierte Flächeninhalt lässt sich mit dem Integral bestimmen. Hier sind noch einmal die Grundideen zusammengestellt.
Zum Herunterladen: orientierteflaecheninhalte2.ggb
Integrale lassen sich also als orientierte Flächeninhalte deuten:
Wenn die Funktion $f$ im Intervall $a \leq x \leq b$ definiert ist, dann entspricht das Integral $I_a(b) = \int\limits_{a}^{b} f(x) \, dx$ geometrisch dem orientierten Flächeninhalt zwischen dem Graphen $G_f$ und der $x$-Achse von $a$ bis $b$.
