Überprüfung - Rekonstruktion eines Bestandes

Aufgabe 1

Voraussetzung: Gehe davon aus, dass der Bestand zu Beginn den Wert $0$ hat, d.h. dass $B(0) = 0$ gilt.

Änderungsrate $B'(x)$	Aussagen über den Bestand $B(x)$	w(ahr) / f(alsch)
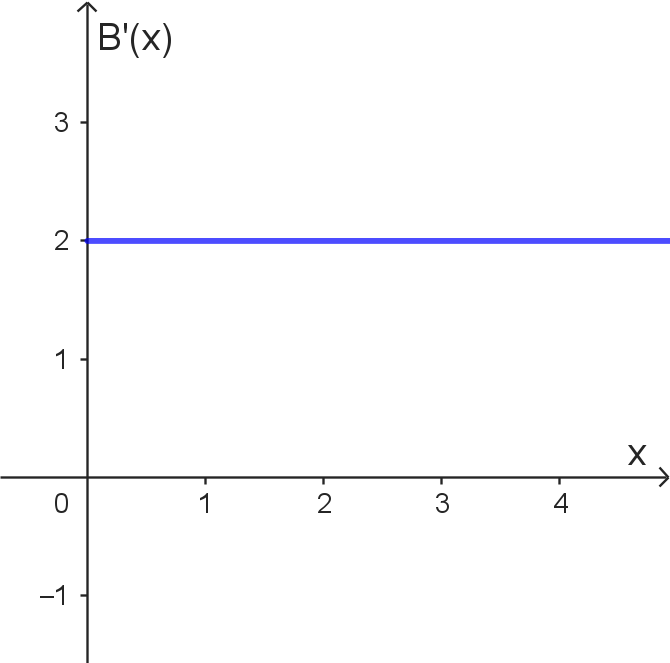	Man berechnet den jeweiligen Bestand hier so: Änderungsrate mal Dauer der Änderung
	$B(4) = 8$
	$B(x)$ ist eine lineare Funktion mit der Steigung $4$.
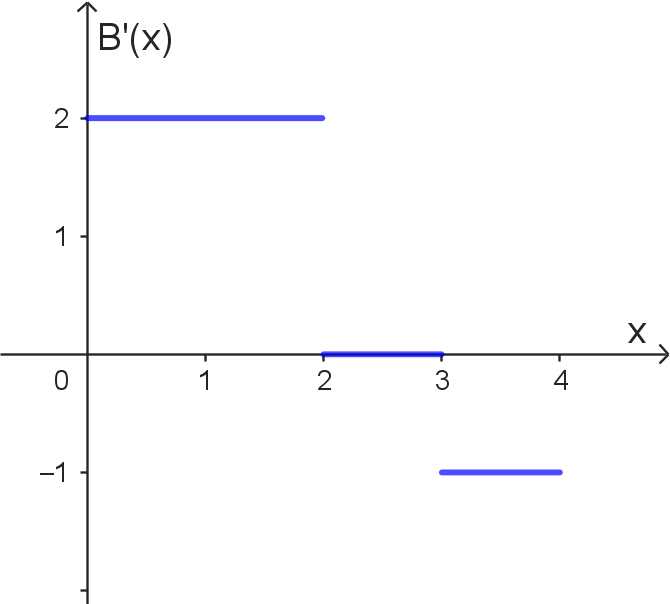	$B(2) > B(1)$
	$B(4) > B(3)$
	$B(3) = B(2)$
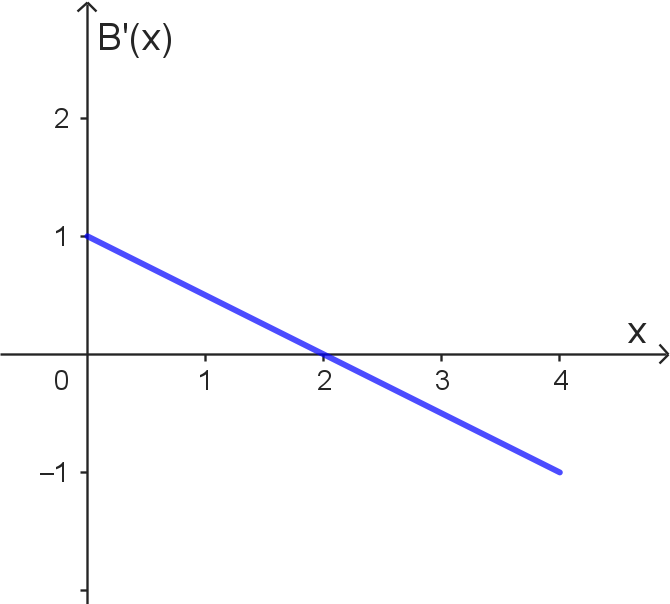	$B(x) > 0$ für alle $x$ mit $0 \leq x \leq 4$
	Die Funktion $B(x)$ ist streng monoton fallend.
	Der Bestand erreicht an der Stelle $x = 2$ einen maximalen Wert.
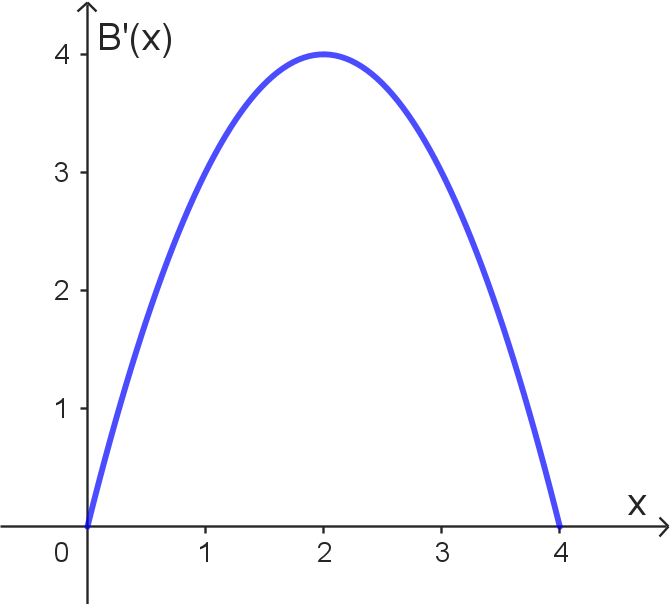	Es gilt folgende Abschätzung: $B(2) \leq 8$
	Mit einer Treppenfunktion mit der Stufenbreite $1$ kann man $B(4)$ so abschätzen: $B(4) \approx B'(0.5)\cdot 1+B'(1.5)\cdot 1+B'(2.5)\cdot 1+B'(3.5)\cdot 1$
	Es gilt: $B'(0)\cdot 1 + B'(1)\cdot 1 \text{ < } B(2) \text{ < } B'(1)\cdot 1 + B'(2)\cdot 1 $