Übungen – Integral und orientierte Flächeninhalte
Aufgabe – Integralwerte geometrisch bestimmen
(i) Bestimme die Integrale (siehe unten), indem du die orientierten Flächeninhalte geometrisch ermittelst.
(ii) Bei welchen Teilaufgaben lassen sich die Eigenschaften des Integrals zu einer effizienten Berechnung des Integralwerts nutzen? Begründe unter Benennung der jeweiligen Eigenschaften.Mit dem Applet unter der Aufgabe kannst du deine Ergebnisse überprüfen.
| Aufgabe | Integralwertberechnung | Veranschaulichung |
|---|---|---|
| (a) | $I_{0}(4) = \int\limits_{0}^{4} x dx = $ | 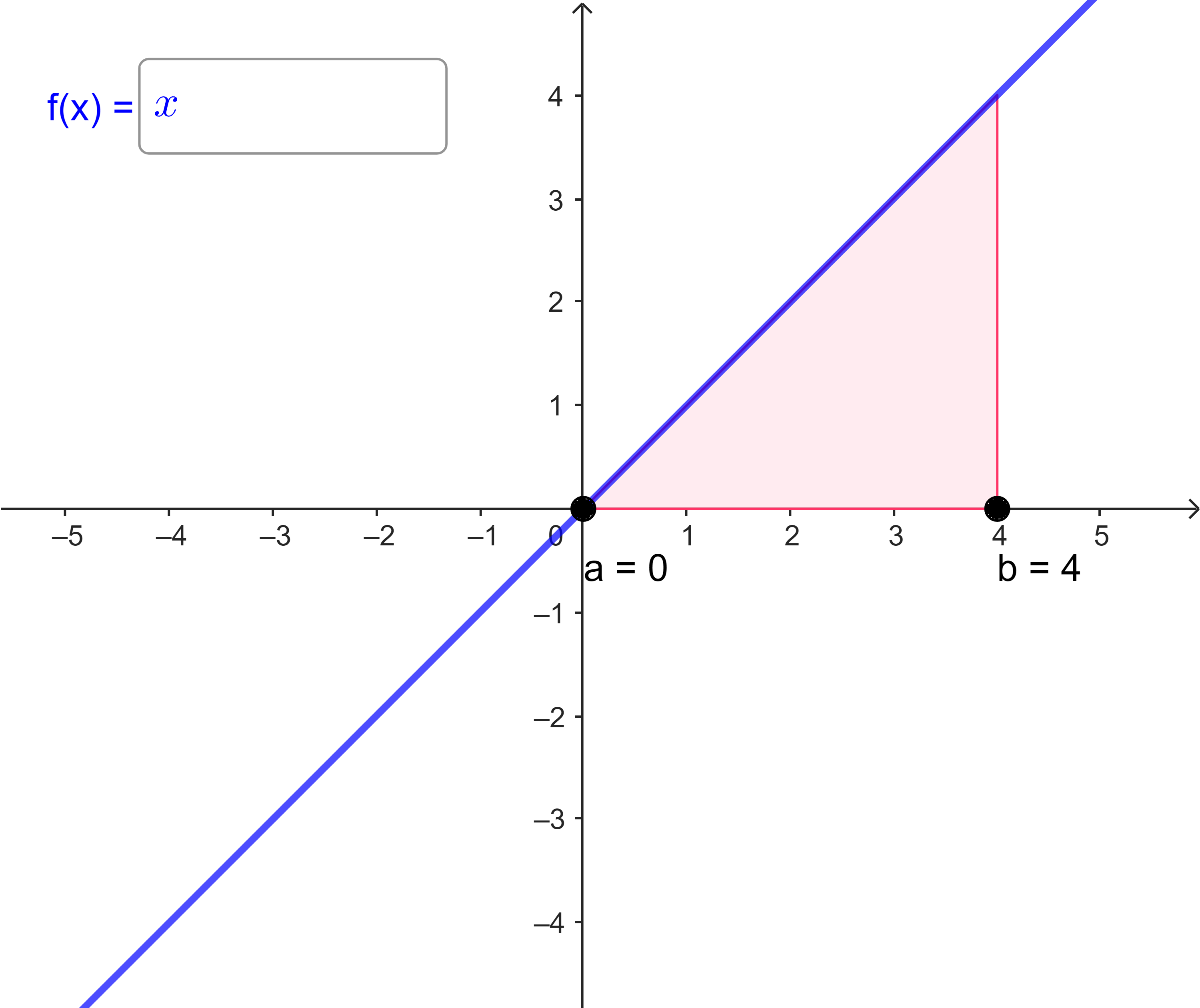 |
| (b) | $I_{0}(2) = \int\limits_{0}^{2} (-2x) dx = $ | 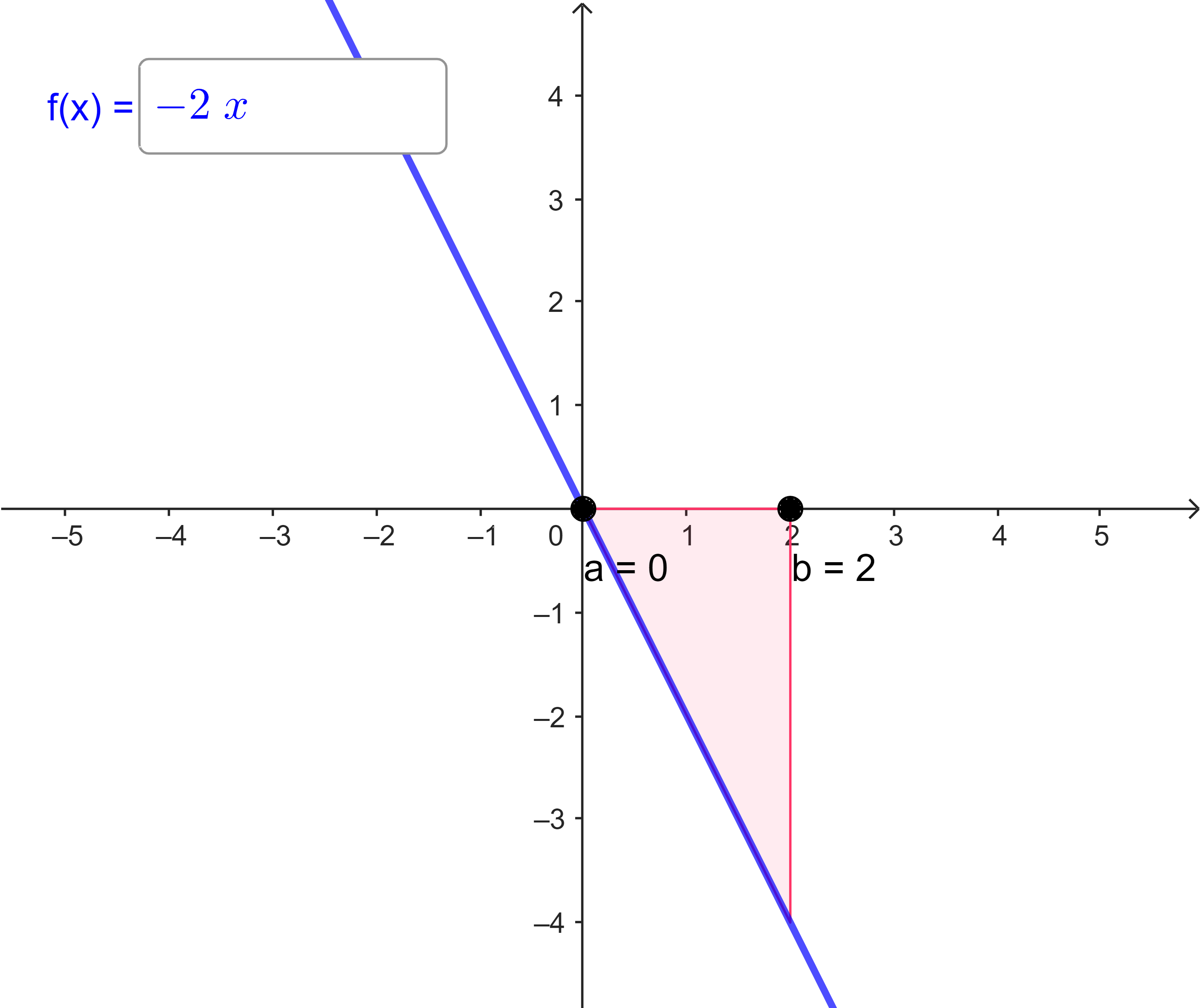 |
| (c) | $I_{-3}(3) = \int\limits_{-3}^{3} (-x) dx = $ | 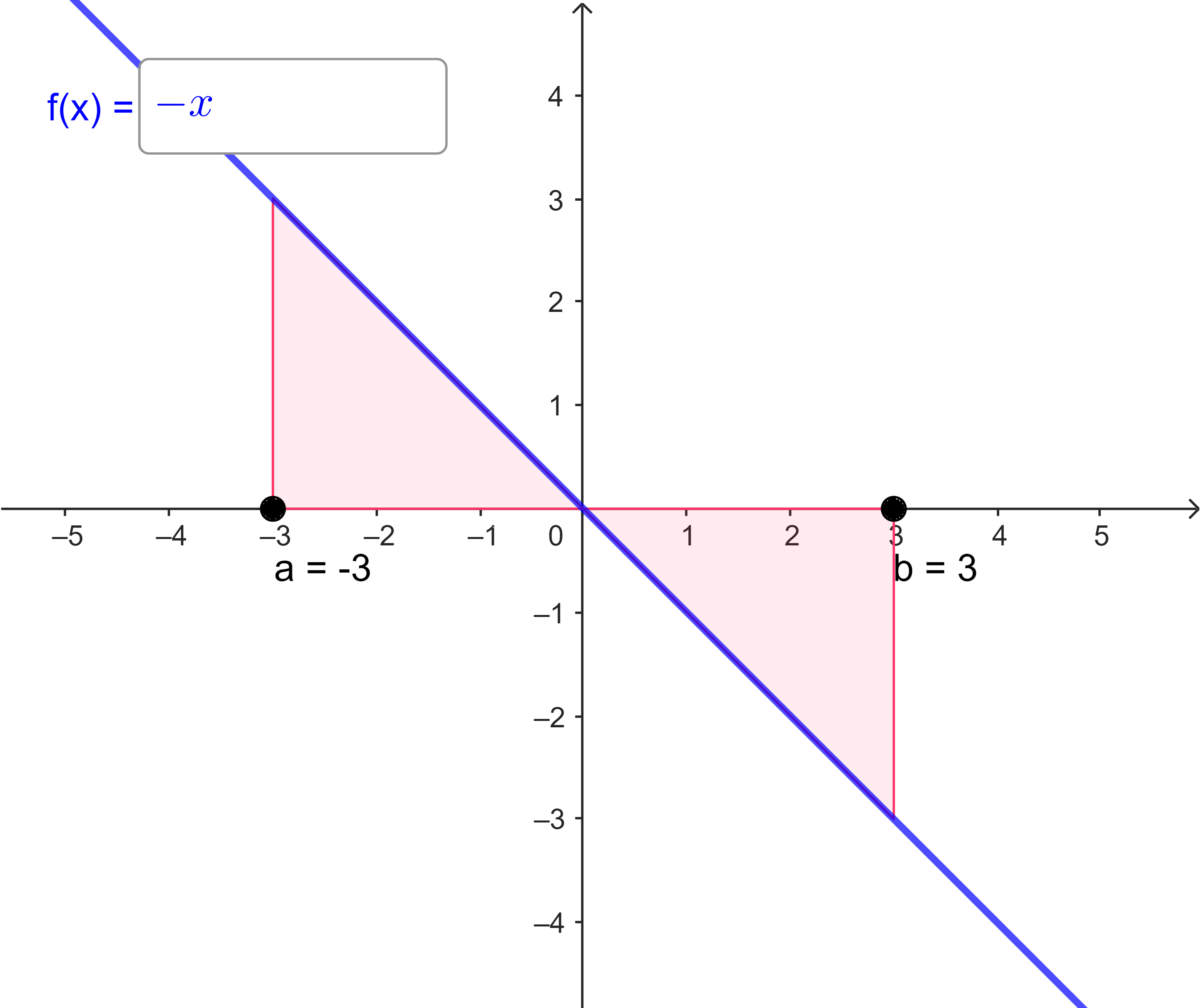 |
| (d) | $I_{-2}(3) = \int\limits_{-2}^{3} 2 dx = $ | 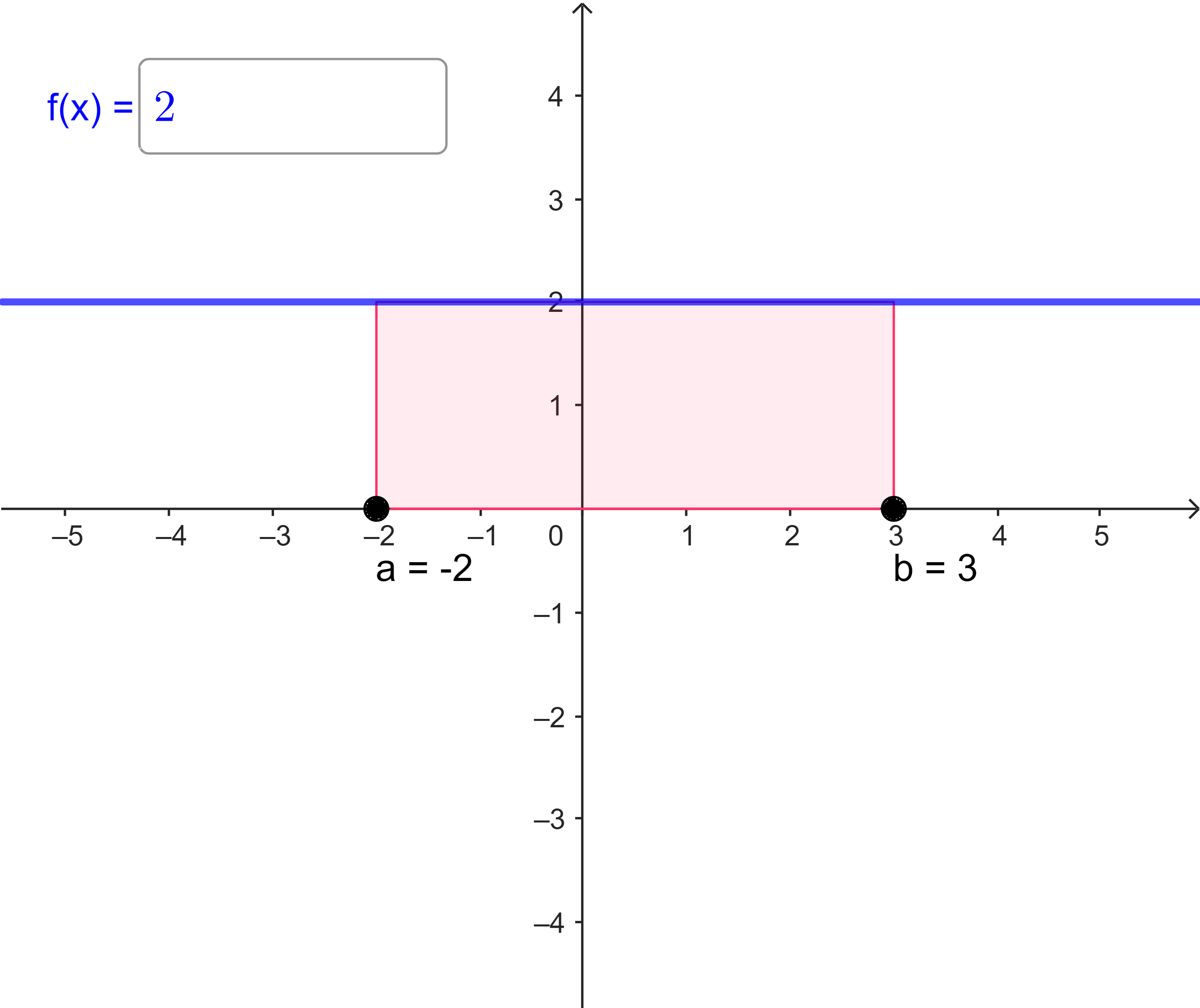 |
| (e) | $I_{-4}(-1) = \int\limits_{-4}^{-1} (-1) dx = $ | 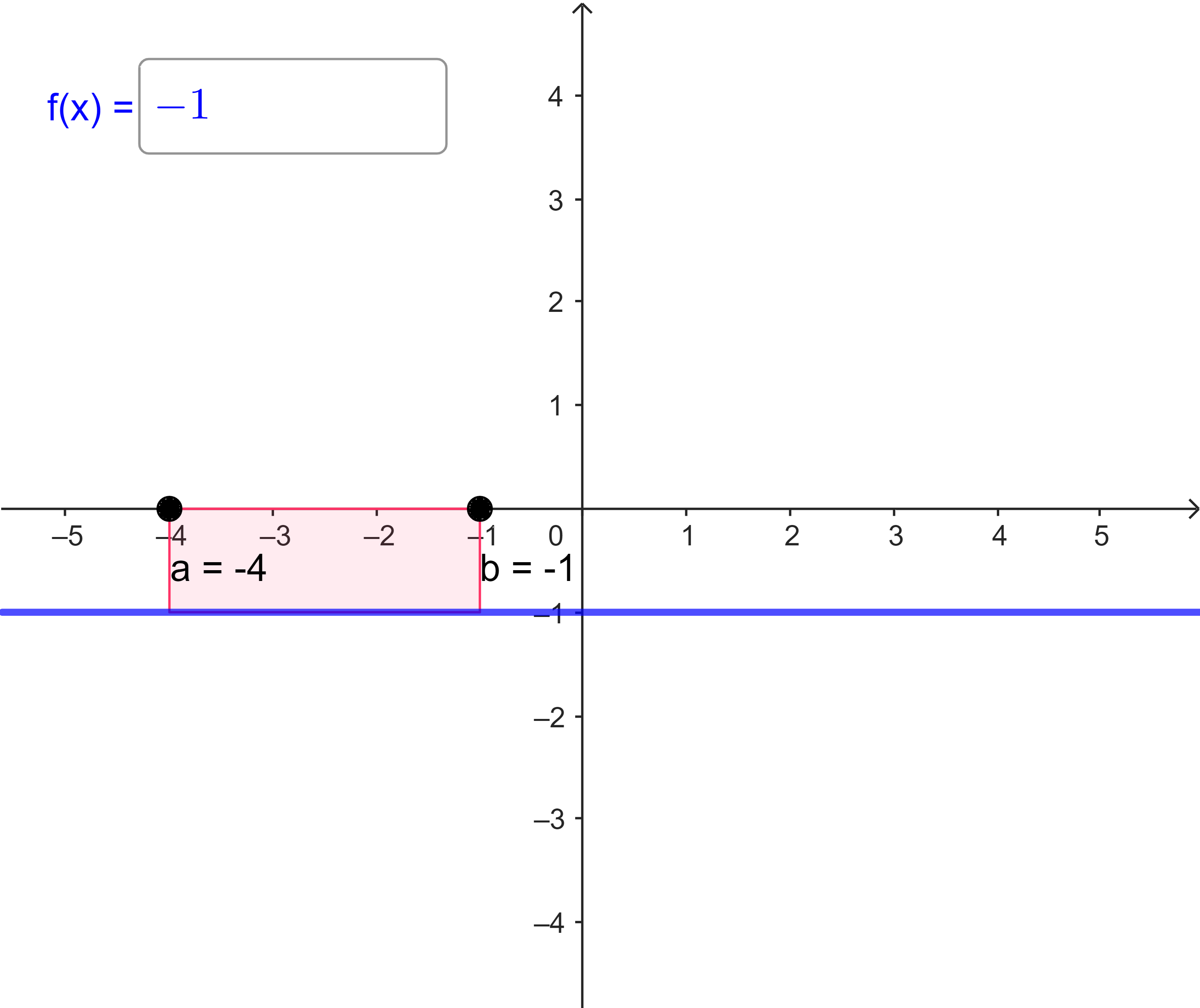 |
| (f) | $I_{-3}(3) = \int\limits_{-3}^{3} (0.5x+1) dx = $ | 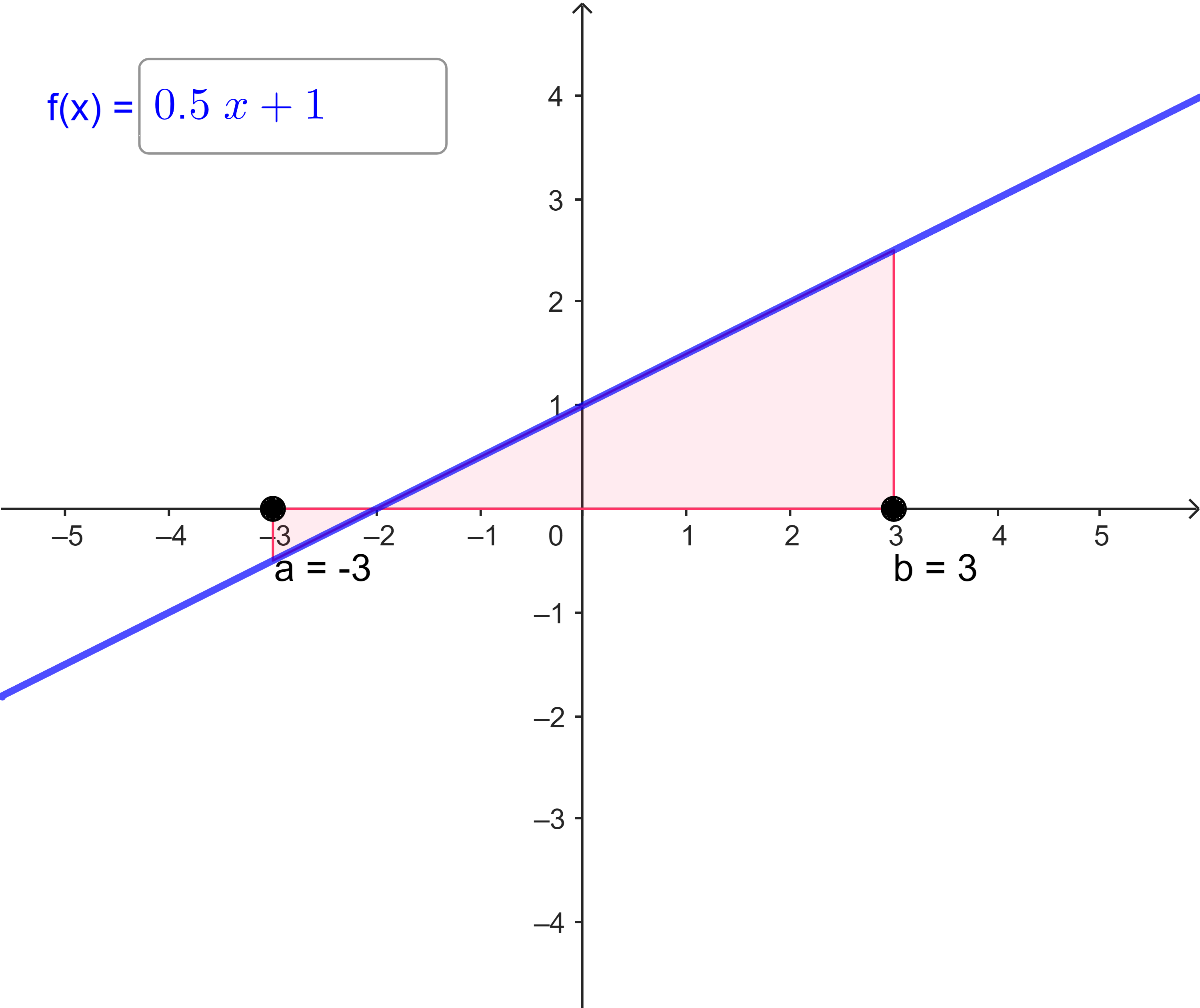 |
| (g) | $I_{0}(2) = \int\limits_{0}^{2} (-x-1) dx = $ | 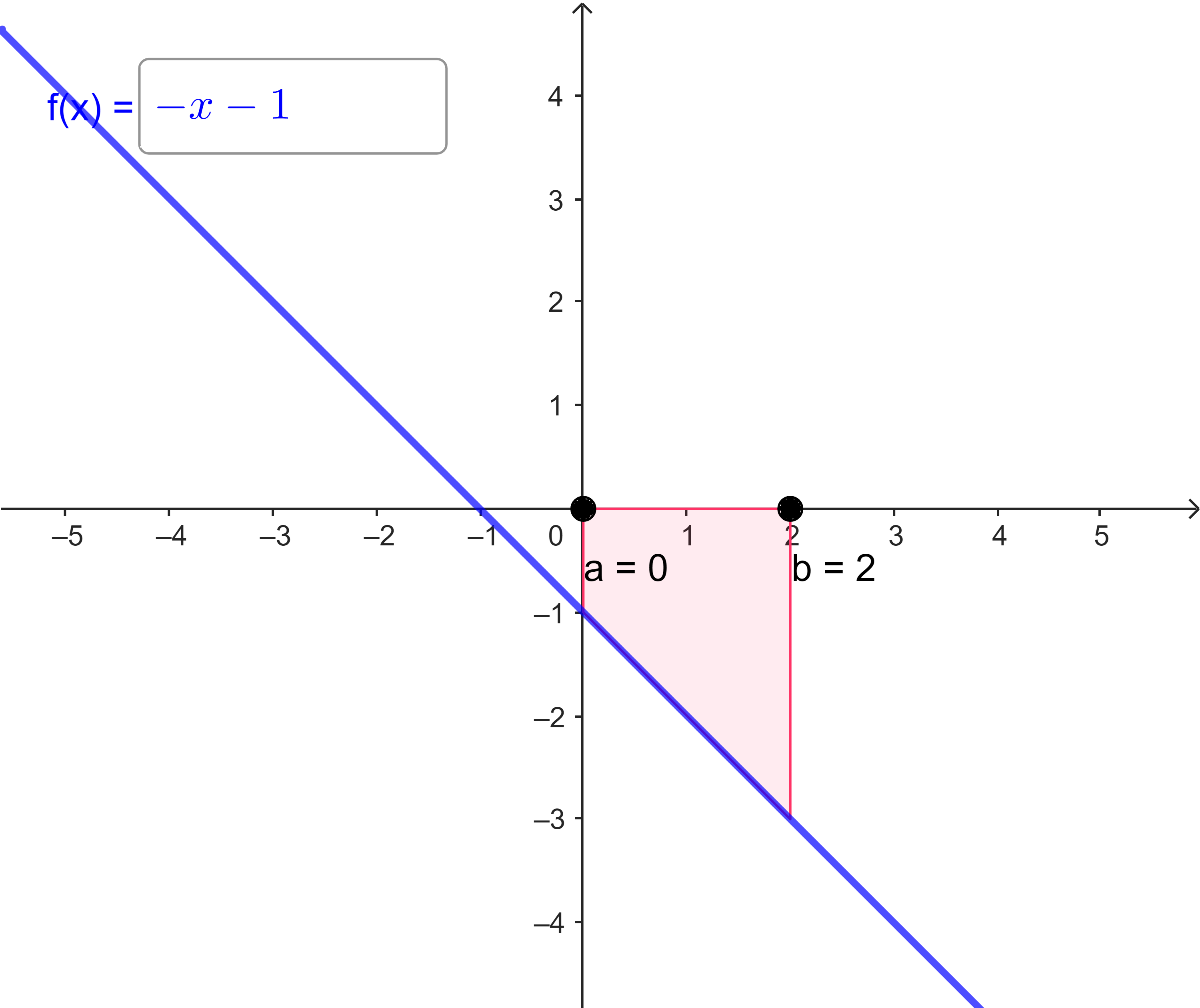 |
| (h) | $I_{-2}(2) = \int\limits_{-2}^{2} (x^3 - 4x) dx = $ | 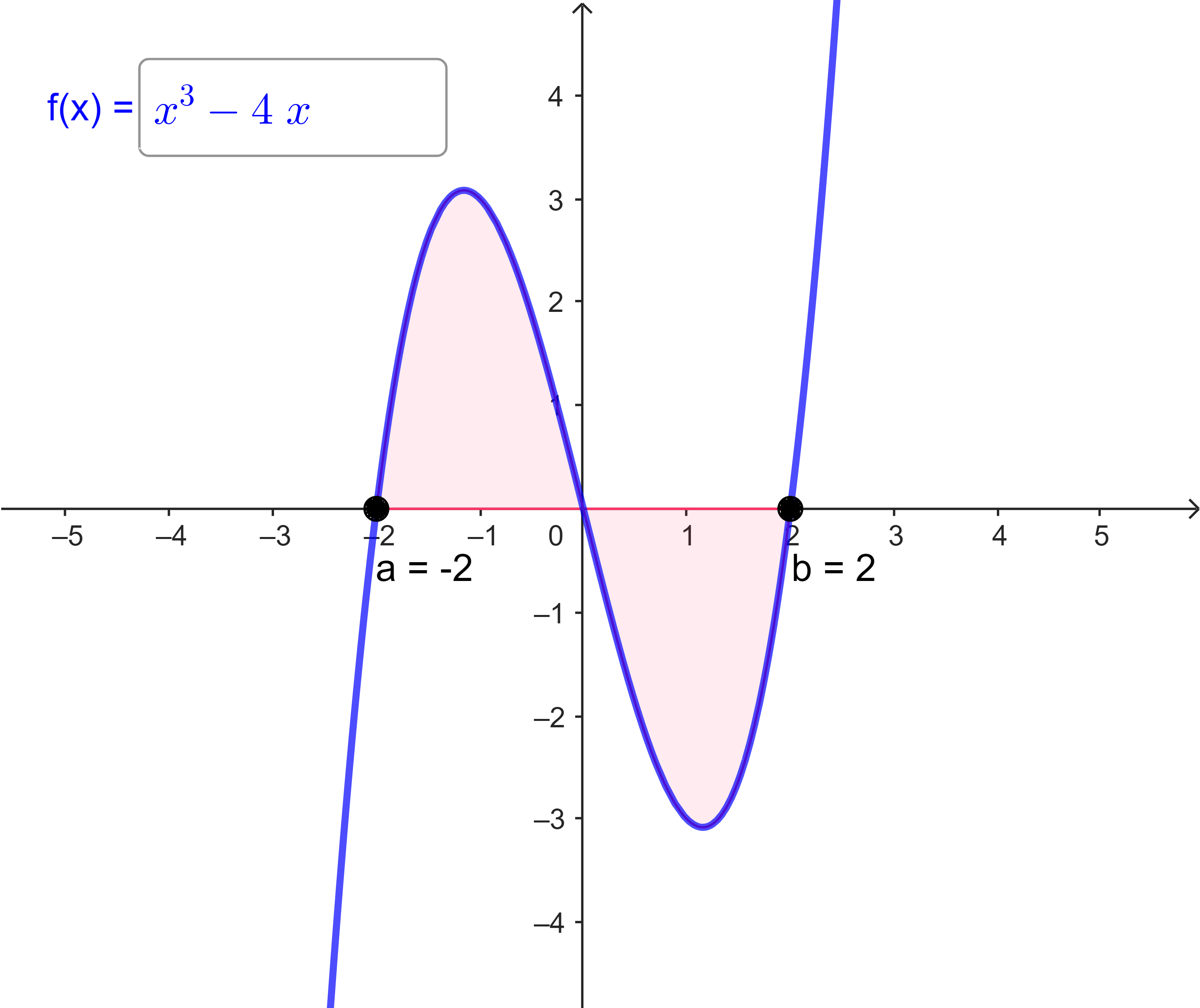 |
Applet zur Kontrolle
Zum Herunterladen: orientierteflaecheninhalte5.ggb

