Hauptsatz der Differential- und Integralrechnung
Worum geht es hier?
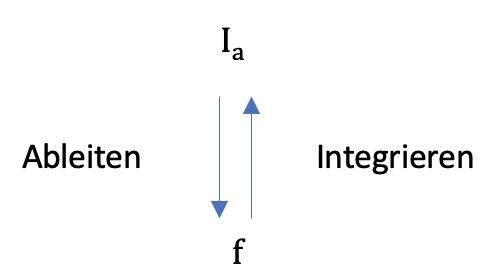
Ableitung und Integral sind zwei fundamentale Konzepte der Differentialrechnung. Während Ableitungen genutzt werden, um Änderungsraten mathematisch zu erfassen, nutzt man das Integral zur Rekonstruktion eines Bestandes. Beide Konzepte hängen eng miteinander zusammen. Ziel dieses Kapitels ist es, diesen Zusammenhang verständlich zu machen und als Hauptsatz der Differential- und Integralrechnung präzise zu beschreiben.
Für dieses Thema musst du ...
- ... mit der geometrischen Deutung des Integrals vertraut sein.
- ... mit Integralfunktionen sicher umgehen können.
- ... mit der Ableitung vertraut sein.
Hier lernst du, ...
- ... wie eine Randfunktion und ihre zugehörigen Integralfunktionen zusammenhängen.
- ... welche Rolle die Ableitung dabei spielt.
Diese Inhalte findest du hier:
- Erkundung — Zusammenhang zwischen Randfunktion und ihren Integralfunktionen
- Strukturierung — Hauptsatz der Differential- und Integralrechnung
- Vertiefung — Beweisskizze zum Hauptsatz
- Übungen — Zusammenhang zwischen Randfunktion und ihren Integralfunktionen
- Überprüfung — Zusammenhang zwischen Randfunktion und ihren Integralfunktionen
- Zusammenfassung — Hauptsatz der Differential- und Integralrechnung

