o-mathe | Erkundung - Berechnung von Integralen » Integralfunktion als Stammfunktion

Integralfunktion als Stammfunktion

Neue Zusammenhänge herstellen

Ziel

Im Laufe dieses Kapitels haben wir schon zwei wichtige Erkenntnisse gewonnen:

Der HDI besagt: Wenn eine Integralfunktion $I_{a}$ zu einer Randfunktion $f$ abgeleitet wird, dann erhalten wir die Randfunktion $f$ .
Außerdem haben wir definiert: Wenn eine Funktion $f$ „aufgeleitet“ wird, erhalten wir eine Stammfunktion $F$ zur Ausgangsfunktion $f$ . Damit konnten wir feststellen: Alle weiteren Stammfunktionen unterscheiden sich von $F$ nur durch eine additive Konstante $c$ .

Ziel soll es nun sein, daraus einen neuen wichtigen Zusammenhang herzustellen, mit dem wir dann Integrale bzw. Integralfunktionen bestimmen können.

Aufgabe 1 (Einstieg)

Begründe mithilfe der bisherigen Erkenntnisse die folgenden neuen Zusammenhänge:

Ist $I_{a} (x)$ eine Integralfunktion zur Randfunktion $f (x)$ , so ist $I_{a} (x)$ eine Stammfunktion von $f (x)$ .

Ist $I_{a} (x)$ eine Integralfunktion zur Randfunktion $f (x)$ und $F (x)$ eine beliebige Stammfunktion von $f (x)$ , so gilt $I_{a} (x) = F (x) + c$ mit einer reellen Zahl $c$ .

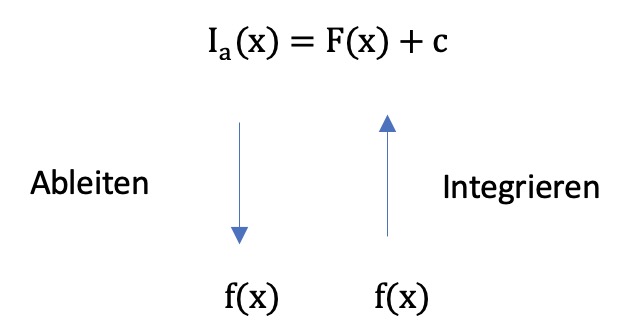
Zusammenhänge ausnutzen

Wir nutzen die neuen Zusammenhänge, um Integralfunktionen zu bestimmen. Dabei wird das folgende Problem bearbeitet:

Problem

Gegeben ist eine Randfunktion $f$ und eine untere Grenze $a$ mit einem $a$ aus dem Definitionsbereich von $f$ .

Gesucht ist die Integralfunktion $I_{a}$ zur Randfunktion $f$ .

Aufgabe 2 (Erarbeitung)

(a) Rechne nach, dass im Applet unten $F$ wirklich eine Stammfunktion von $f$ darstellt.

(b) Begründe, dass das voreingestellte $F$ nicht die gesuchte Integralfunktion darstellt.

💡 Tipp

Verschiebe dafür $x$ geeignet, um zu verdeutlichen, dass die im unteren Feld markierten Werte von $I_{a}$ nicht zum Graphen oben passen.

(c) Es gibt eine bestimmte Stelle $x$ , für die $I_{a} (x)$ immer bekannt ist. Nutze diese Stelle, um die Zahl $c$ mit dem Schieberegler korrekt einzustellen. Kontrolliere dein Ergebnis, indem du das Kontrollkästchen aktivierst.

Wie funktioniert das Applet?

Klicke erst einmal nicht auf das Kontrollkästchen „Integralfunktion $I_{a} (x)$ “!

Lasse im Applet erst einmal $f (x)$ und $a$ unverändert und verschiebe nur die Stelle $x$ im unteren Fenster sowie den Schieberegler $c$ im oberen Fenster.

Zum Herunterladen: integralfunktionalsstammfunktion1.ggb

Aufgabe 3 (Erarbeitung)

Begründe den folgenden Zusammenhang:

Ist $I_{a}$ eine Integralfunktion zur Randfunktion $f$ und $F$ eine beliebige Stammfunktion von $f$ , so gilt $I_{a} (x) = F (x) - F (a)$ .

Aufgabe 4 (Sicherung)

🖊️ Notiere dir die Begründungen im Wissensspeicher (Box „Argumentationskette“).

💡 Tipp

Benutze die Eigenschaft von Integralfunktionen, die du in Aufgabe 2 (c) gefunden hast.

Unbestimmte Integrale

Der Zusammenhang von oben führt dazu, dass man die Menge aller Stammfunktionen von $f$ auch als unbestimmtes Integral bezeichnet. Man nutzt dafür auch die Integralschreibweise $\int$ , aber ohne Integrationsgrenzen:

$\underset{Unbestimmtes Integral}{\underset{⏟}{\int f (x) d x}} = \underset{Stammfunktion}{\underset{⏟}{F (x)}} + \underset{Integrationskonstante}{\underset{⏟}{c}}$

Für ein Integral mit Integrationsgrenzen, also $\int_{a}^{b} f (x) d x$ nutzt man auch den Begriff bestimmtes Integral.

Aufgabe 5 (Vertiefung)

(a) Erkläre die Begriffe „bestimmtes“ und „unbestimmtes“ Integral.

(b) 🖊️ Halte die Definition eines unbestimmten Integrals im Wissensspeicher fest.

(c) Ändert sich das Ergebnis eines bestimmten Integrals mit der Formel $\int_{a}^{b} f (x) d x = F (x) - F (a)$ , wenn man die Stammfunktion $F$ durch eine andere Stammfunktion austauscht? Begründe.

←Zurück Weiter→