Zusammenfassung – Stammfunktionen
Grundidee und Präzisierung
Ableiten und "Aufleiten" sind zwei inverse Operationen. Durch die jeweilige Operation entsteht aus einer Funktion jeweils eine andere Funktion.
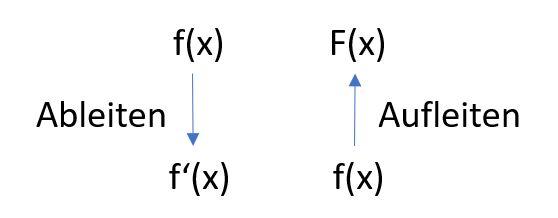
Beim Ableiten entsteht aus einer Ausgangsfunktion $f$ eine Ableitungsfunktion $f'$. Beim "Aufleiten" entsteht aus einer Ausgangsfunktion $f$ eine Funktion $F$, die als Stammfunktion von $f$ bezeichnet wird.
Eine Funktion $F$ wird Stammfunktion von $f$ genannt genau dann, wenn $f$ die Ableitungsfunktion von $F$ ist.
Also wenn $F' = f$ gilt.
Das Applet verdeutlicht eine Situation mit einer Ausgangsfunktion $f$ und einer zugehörigen Stammfunktion $F$:
Zum Herunterladen: stammfunktionen3.ggb
Bestimmung von Stammfunktionen
Bei der Bestimmung von Stammfunktionen wird das folgende Problem bearbeitet:
Gegeben ist eine Ausgangsfunktion $f$.
Gesucht ist eine Stammfunktion $F$ von $f$ (d.h. es muss $F' = f$ gelten).
Bei ganzrationalen Funktionen ist die Bestimmung von Stammfunktionen recht einfach: Integriert wird, indem die Ableitungsregeln umgekehrt anwendet werden.
$\begin{array}{ccl} F(x) & = & \frac{1}{5}x^5 + 2 \cdot \frac{1}{4} x^4 - \frac{1}{2} \cdot \frac{1}{3} x^3 + \frac{1}{2} x^2 - 1 \cdot x = \frac{1}{5}x^5 + \frac{1}{2} x^4 - \frac{1}{6} x^3 + \frac{1}{2} x^2 - x \\ \uparrow & & \\ f(x) & = & x^4 + 2 x^3 - \frac{1}{2} x^2 + x - 1 \end{array}$
Hierbei wird u.a. die folgende Regel für Potenzfunktionen genutzt:
Wenn $f(x) = x^n$, $n\in\mathbb{N}$, dann ist $F$ mit $F(x) = \frac{1}{n+1} x^{n+1}$ eine Stammfunktion von $f$.
Gesamtheit aller Stammfunktionen
Wenn $F$ eine Stammfunktion von $f$ ist, dann erhält man weitere Stammfunktionen, indem man additive Konstanten hinzufügt, welche beim Ableiten wieder wegfallen. Meist wird dies folgendermaßen dargestellt:
$\begin{array}{cclll} F(x) & = & \frac{1}{5}x^5 + \frac{1}{2} x^4 - \frac{1}{6} x^3 + \frac{1}{2} x^2 - x + c & \text{mit} & c \in \mathbb{R} \\ \uparrow & & \\ f(x) & = & x^4 + 2 x^3 - \frac{1}{2} x^2 + x - 1 \end{array}$
Es gelten die folgenden Sätze über Stammfunktionen:
(A) Wenn die Funktion $F$ eine Stammfunktion von $f$ ist, ist auch die Funktion $G$ mit $G(x) = F(x) + c$ mit $c\in\mathbb{R}$ eine Stammfunktion von $f$ .
(B) Wenn die Funktionen $F$ und $G$ Stammfunktionen von $f$ sind, unterscheiden sie sich nur durch eine additive Konstante, d.h. es gibt eine reelle Zahl $c$ so, dass $F(x) = G(x) + c$ für jedes $x \in\mathbb R$ gilt.
Satz A ist direkt einsichtig, da beim Ableiten die additive Konstante wieder wegfällt.
Satz B lässt sich auch leicht begründen:
Wenn $F$ und $G$ Stammfunktionen von $f$ sind, dann gilt $F'(x) = f(x)$ und $G'(x) = f(x)$ für jedes $x \in\mathbb R$.
Für die Hilfsfunktion $H$ mit $H(x) = F(x) - G(x)$ gilt dann: $H'(x) = F'(x) - G'(x) = f(x) - f(x) = 0$ für jedes $x \in\mathbb R$.
Die Funktion $H$ hat demnach
überall die Steigung $0$.
Es ist plausibel, dass der Graph der Funktion $H$ dann eine Parallele zur $x$-Achse darstellt bzw. dass
die Funktion $H$ eine konstante Funktion mit $H(x) = c$ für ein $c\in\mathbb R$ ist. Also gilt $F(x) - G(x) = c$ für jedes $x \in\mathbb R$.
Die Stammfunktionen $F$ und $G$ unterscheiden sich folglich nur durch eine additive Konstante $c$.
Umgangssprachliche Formulierung der beiden Teilsätze
Satz A: "Kennt man eine Stammfunktion von einer Ausgangsfunktion, dann kennt man unendlich viele Stammfunktionen zur Ausgangsfunktion."
Satz B: "Kennt man eine Stammfunktion von einer Ausgangsfunktion, dann kennt man alle Stammfunktionen zur Ausgangsfunktion."
