Integralberechnung
Eine Stammfunktion verwenden
Wir haben den folgenden Zusammenhang zwischen Integralfunktionen und Stammfunktionen zu einer Randfunktion hergestellt:
Ist $I_a$ eine Integralfunktion zur Randfunktion $f$ und $F$ eine beliebige Stammfunktion von $f$, so gilt $I_a(x) = F(x) - F(a)$.
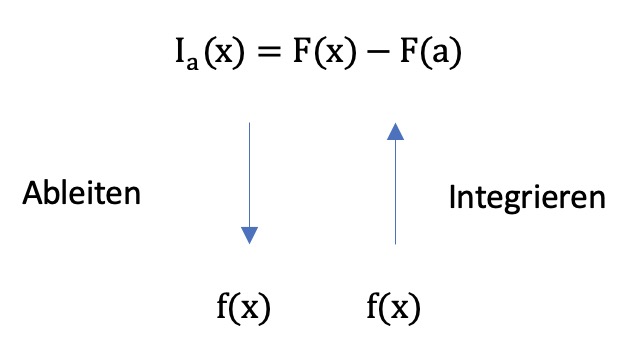
Wir nutzen diesen Zusammenhang, um Integrale zu berechnen:
Zum Herunterladen: integralfunktionalsstammfunktion2.ggb
Betrachte die folgende Situation:
Problem
Gegeben ist eine Randfunktion $f$ und ein Intervall $a \leq x \leq b$ (das in der Definitionsmenge von $f$ liegt).
Gesucht ist das Integral $I_a(b)$ zur Randfunktion $f$.
Aufgabe 1 (Erarbeitung)
Begründe mithilfe des Applets:
Wir erhalten $I_a(b)$, indem wir eine Stammfunktion $F$ zur Randfunktion $f$ bestimmen und Folgendes berechnen: $I_a(b) = F(b) - F(a)$.
Aufgabe 2 (Erarbeitung)
(a) Erläutere die Integralberechnung in der ersten Zeile der Tabelle.
(b) Berechne analog die Stammfunktionen und Integrale in den weiteren Zeilen der Tabelle.
| Randfunktion $f$ | Stammfunktion $F$ | Integral $I_a(b)$ |
|---|---|---|
| $f(x) = -\frac{3}{5}x^2+2x$ | $F(x) = -\frac{1}{5}x^3+x^2$ | $\begin{array}{ccl} I_1(4) & = & F(4) - F(1) \\ & = & 3.2 - 0.8 \\ & = & 2.4 \end{array}$ |
| $f(x) = x^2$ | $F(x) = \dots $ | $I_1(3) = \dots $ |
| $f(x) = 2-0.5x$ | $F(x) = \dots $ | $I_{-1}(2) = \dots $ |
| $f(x) = -\frac{1}{3}x^3+2x$ | $F(x) = \dots $ | $I_{-1}(1) = \dots $ |
| $f(x) = x^4$ | $F(x) = \dots $ | $I_{0}(1) = \dots $ |

