Inhaltliche Betrachtungen
Bestandsentwicklungen betrachten
Wir betrachten folgende Situation:
Die Funktion $B$ beschreibt die Entwicklung eines Bestandes (z.B. die Entwicklung der Wassermenge in einem Zufluss-Abfluss-System).
Die Funktion $B'$ beschreibt die momentanen Änderungen eines Bestandes (z.B. die Entwicklung der momentanen Zuflussrate in einem Zufluss-Abfluss-System).
Änderungsratenfunktion $B'$ aus der Bestandsfunktion $B$ bestimmen
Im Kapitel Ableitungenhast du gesehen, dass sich die Änderungsratenfunktion $B'$ aus der Bestandsfunktion $B$ durch Ableiten ergibt. Die Ableitung kann dabei geometrisch als lokale Steigung der Bestandsfunktion gedeutet werden.
Aufgabe 1 (Einstieg)
Verdeutliche den Zusammenhang anhand des Applets, indem du $x$ variierst.
Zum Herunterladen: differenzieren1.ggb
Bestandsfunktion $B$ aus der Änderungsratenfunktion $B'$ rekonstruieren
Im Kapitel Rekonstruktion eines Bestandeshast du gesehen, dass aus einer vorgegebenen Änderungsratenfunktion $B'$ die Bestandsfunktion $B$ rekonstruiert werden kann, indem Produktsummen für immer feinere Unterteilungen des betrachteten Intervalls bestimmt werden. Solche Grenzwerte von Produktsummen werden als Integrale bezeichnet und können geometrisch als orientierte Flächeninhalte gedeutet werden.
Aufgabe 2 (Einstieg)
Verdeutliche den Zusammenhang anhand des Applets, indem du $x$ variierst.
Zum Herunterladen: integrieren2.ggb
Zusammenhang zwischen der Bestandsfunktion $B$ und der Änderungsratenfunktion $B'$ formulieren
Die Grafik verdeutlicht den fundamentalen Zusammenhang zwischen der Bestandsfunktion $B$ und der Änderungsratenfunktion $B'$.
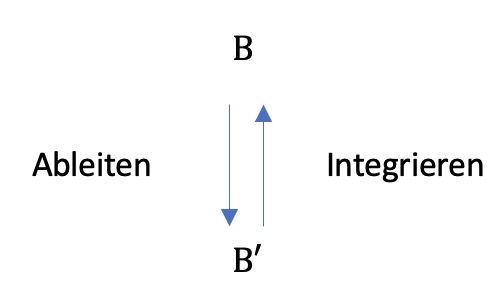
- $B'$ entsteht aus $B$ durch Ableiten.
- $B$ entsteht aus $B'$ durch Integrieren.
Aufgabe 3 (Einstieg)
Basierend auf dem gezeigten Zusammenhang eröffnet sich eine neue Möglichkeit, wie $B$ aus $B'$ rekonstruiert werden kann. Skizziere einen Vorschlag.

