„Aufleitungen“

Das Ziel festlegen

Im letzten Kapitel wurde gezeigt, wie eine Randfunktion und ihre zugehörigen Integralfunktionen zusammenhängen: Wenn eine Integralfunktion $I_a$ zu einer Randfunktion $f$ abgeleitet wird, erhalten wir die Randfunktion $f$.

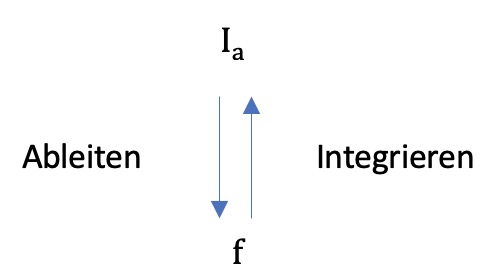
Das Applet verdeutlicht diesen Zusammenhang anhand eines Beispiels:

Zum Herunterladen: integrieren6.ggb

Dieser Zusammenhang kann bei der Bestimmung von Integralfunktionen genutzt werden. Dabei wird das Ableiten umgekehrt, indem die vorgegebene Randfunktion integriert wird.

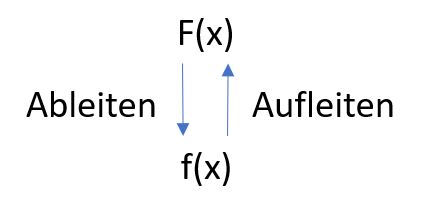
Für "Aufleitungen" einer vorgegebenen Funktion wird ein neuer Begriff eingeführt.

Ziel der folgenden Abschnitte ist es herauszufinden, wie Stammfunktionen einer Ausgangsfunktion bestimmt werden.