Ableitung an einer Stelle

Worum geht es hier?

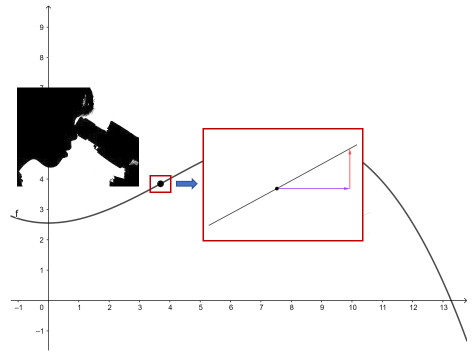
Die bisher gewonnenen Erkenntnisse zur lokalen Änderungsrate werden hier mit verallgemeinernd dem Ableitungsbegriff beschrieben. Ziel ist es, die bereits bekannten Zusammenhänge weiter zu vertiefen. Hierbei steht die geometrische Deutung der lokalen Änderungsrate im Vordergrund.

Für dieses Thema musst du ...

• ... sicher mit Funktionen umgehen können.
• ... das Konzept der lokalen Änderungsrate verstanden haben.

Hier lernst du, ...

• ... was man unter einer Ableitung versteht.
• ... wie man eine Ableitung an einer Stelle experimentell bestimmt.
• ... wie man eine Ableitung an einer Stelle geometrisch als Steigung des Funktionsgraphen in einem Punkt deutet.
• ... wie man eine Ableitung an einer Stelle zur Konstruktion von Tangenten an den Funktionsgraphen nutzt.

Hier geht's zur Konzeption des Kapitels.