Höhere Ableitungen

Aufgabe 1

Die Tabelle zeigt Information (gerundete Werte) über die Funktion $f$ mit $f(x)=\frac{1}{150}{x}^5-\frac{8}{45}{x}^3$.

(a) Bestimme mit dieser Information folgende besondere Punkte von Graph $f$:

• Schnittpunkte mit der $x$-Achse und der $y$-Achse
• Hoch- und Tiefpunkte
• Wendepunkte / Sattelpunkte

Beachte, dass die Tabelle auch Information enthält, die für die Bestimmung der besonderen Punkte nicht benötigt wird. Gib jeweils genau an, wie du (mit einem passenden Kriterium) argumentierst.

(b) Skizziere mit den Ergebnissen aus (a) den Graph von $f$.

Kontrolliere mit dem Funktionenplotter. Gib hierzu den Funktionsterm $f(x)=\frac{1}{150}{x}^5-\frac{8}{45}{x}^3$ mit einem passenden Bereich (siehe Tabelle oben) in den Plotter ein.

Zum Herunterladen: plotter2.ggb

Aufgabe 2

Die folgende Grafik zeigt Information über eine Funktion $f$ und ihre Ableitungen.

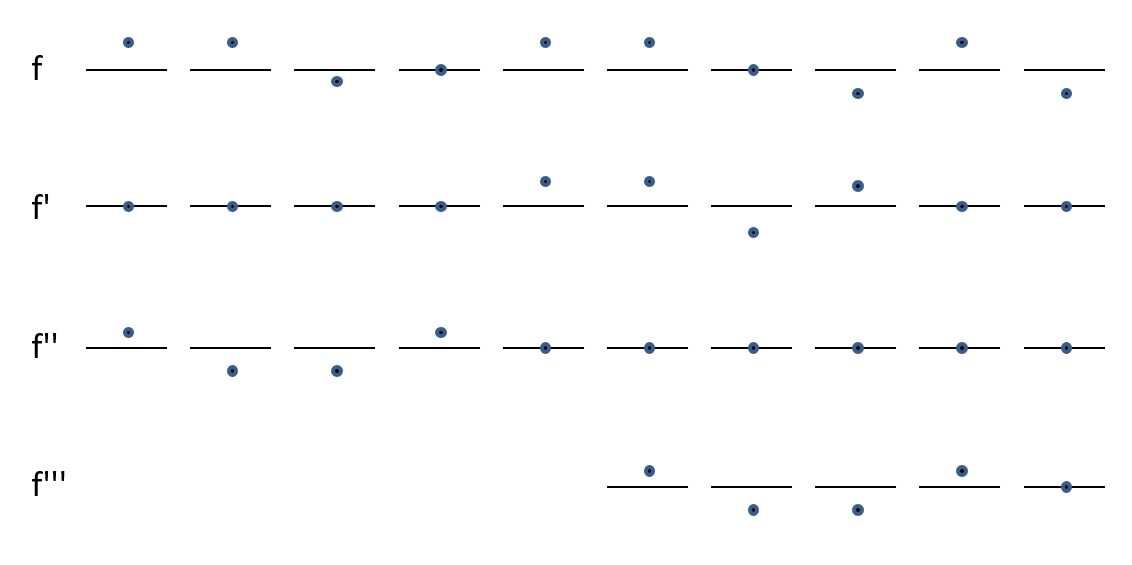
Deute jeweils den Verlauf von Graph f in einer Umgebung des eingezeichneten Punktes an.

Tipp: Beginne jeweils beim unteren Graphen. Im ersten Beispiel kann man ablesen, dass hier $f^{″}(x)>0$ gilt. Der Graph von $f^{\prime }$ muss also in einem kleinen Bereich um $x$ steigen. Da $f^{\prime }(x)=0$ auch vorgegeben ist, muss an der Stelle $x$ eine Nullstelle mit einem $-/+$-Vorzeichenwechsel vorliegen. Mit diesem Wissen kann man zunächst den Graph von $f^{\prime }$ in einem Bereich um $x$ andeuten. Weiter kann man schließen, dass $f$ an der betreffenden Stelle $x$ einen Tiefpunkt haben muss. Den kann man jetzt im obersten Koordinatensystem (mit einen kleinen Bogen) andeuten.

Aufgabe 3

Bestimme jeweils die Wendepunkte von $f$. Zur Kontrolle kannst du den Funktionenplotter oben benutzen.

(a) $f(x)=x^3+3x^2+1$

(b) $f(x)=\frac{1}{12}{x}^4-2x^2$

(c) $f(x)=3x^5-5x^3$