Vertiefung
Zur Orientierung
Hier sollst du das im letzten Abschnitt benutzte Verfahren zu Kostenminimierung auf ein weiteres Kostenminimierungsproblem anwenden.
Das analytische Minimierungsverfahren beurteilen
Betrachte die folgende Ausgangssituation:
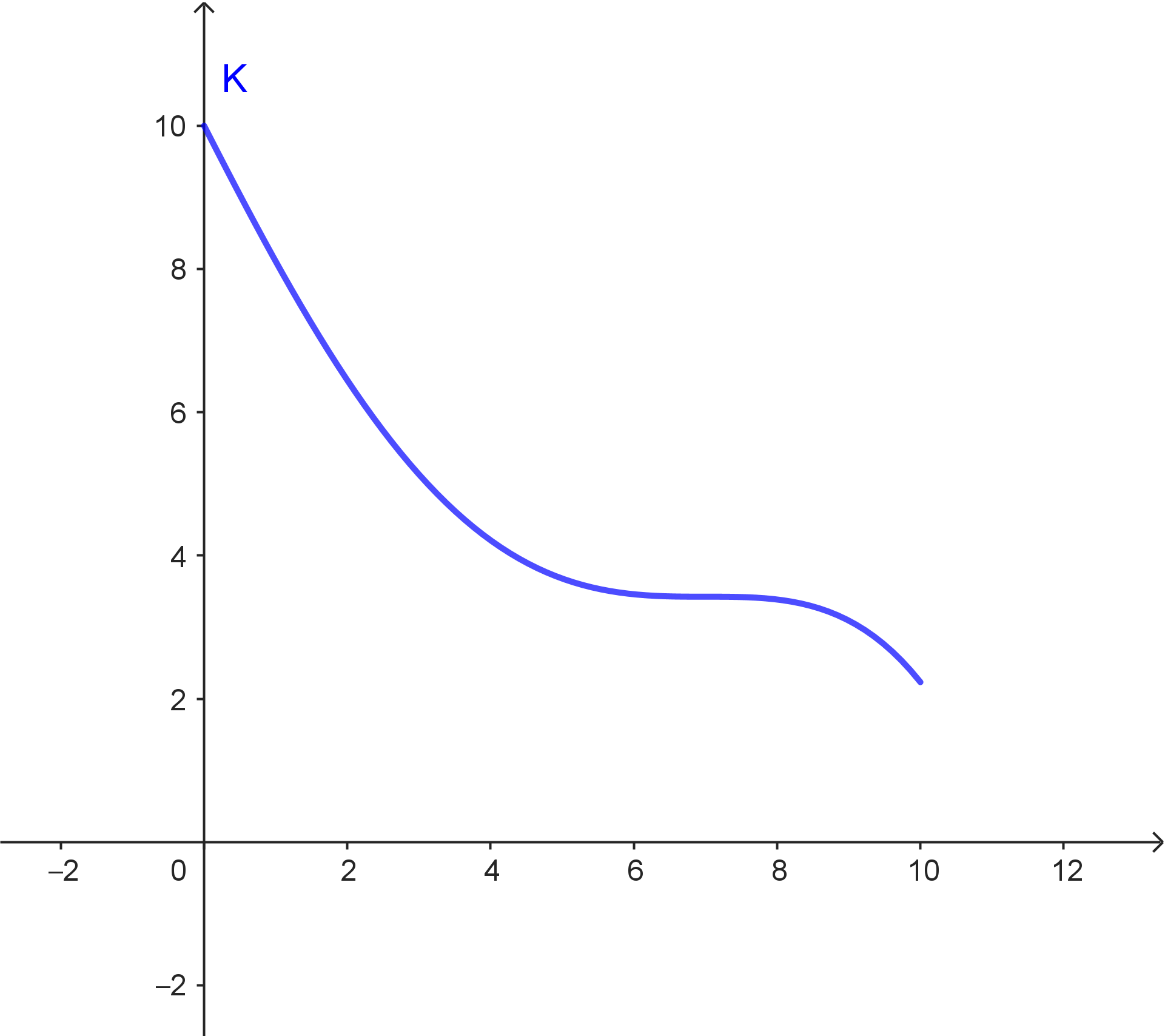
Wenn der Betrieb $x$ Mengeneinheiten Teile produziert (wobei $0 \leq x \leq 10$ gelten soll), dann entstehen dem Betrieb Kosten von $K(x)$ Geldeinheiten. Für die Kostenfunktion gilt:
$K(x) = -\frac{1}{400}x^4 + \frac{1}{30}x^3 + \frac{7}{200}x^2 - \frac{49}{25}x + 10$
Für welche Mengeneinheit entstehen dem Betrieb die geringsten Kosten?
Aufgabe 1
Gehe genauso wie im letzten Abschnitt vor und bestimme das lokale Minimum der Funktion $K(x)$ im Intervall $0 \leq x \leq 10$ mit Hilfe der Ableitung.
Aufgabe 2
Kontrolliere deine Lösung mit dem Graph der Kostenfunktion.
Graph der Kostenfunktion
Aufgabe 3
Erläutere die Schwierigkeit, die bei der Verwendung der Ableitung beim Lösen von Optimierungsproblemen entsteht.
