Aufgabe 6
Aufgaben
Gegeben ist der Graph einer ganzrationalen Funktion $f$ vom Grad $4$.
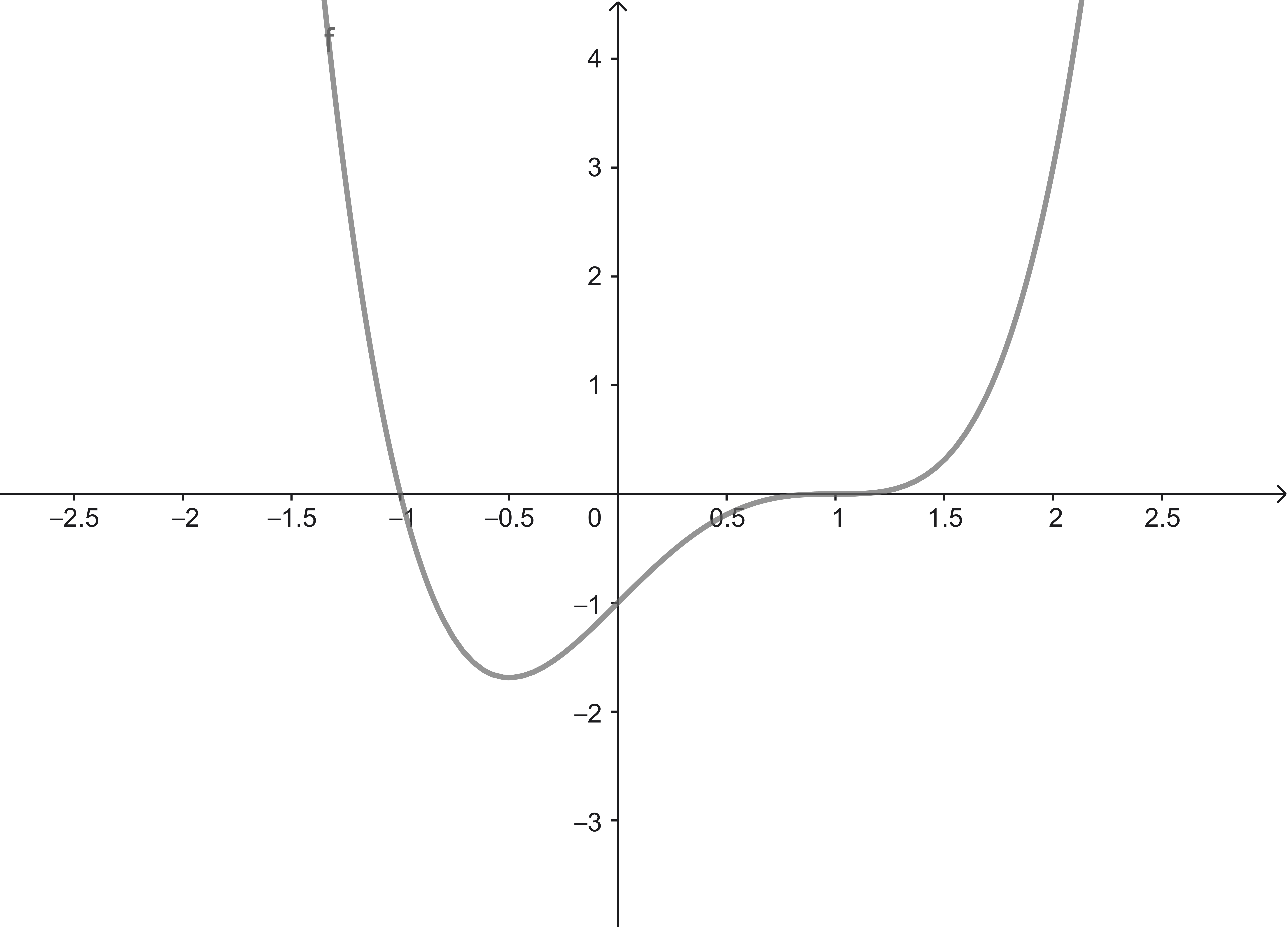
(a) Skizziere den Verlauf von Graph $f'$ und Graph $f''$.
(b) Jeweils eine der folgenden Funktionsgleichungen passt zum vorgegebenen Graph. Ermittle und begründe (ohne Rechnungen), welche Funktionsgleichung das ist.
- $f(x) = (x+1)(x-1)^3$ oder $f(x) = x^2(x-1)^2$ oder $f(x) = (x+1)^2(x-1)^2$
- $f'(x) = 4(x+0.5)(x-1)^2$ oder $f'(x) = 2(x+1)(x-1)^2$ oder $f(x) = (x+0.5)(x-1)$
- $f''(x) = 8(x-1)^2$ oder $f''(x) = 12x(x-1)$ oder $f''(x) = 4(x-1)$
(c) Wieso hat $f$ die folgenden Eigenschaften? Begründe jeweils.
- $f'(0) > 0$
- $f(3) > 0$
- $f''(-1) > 0$

