Vorzeichenwechselkriterium
Aufgabe 1
Gegeben ist eine Tabelle mit Eigenschaften von $f'$. Gesucht sind die zugehörigen Eigenschaften von $f$ und eine Skizze eines passenden Graphen.
(a) Vervollständige die Tabelle und zeichne einen passenden Graph $f$ mit diesen Eigenschaften.
| Stelle / Intervall | $f'(x)$ | Vorzeichen/VZW | Eigenschaft von $f$ |
|---|---|---|---|
| $-\infty \text{ < } x \text{ < } -1$ | $f'(x) > 0$ | $+$ | $f$ streng monoton wachsend |
| $x = -1$ | $f'(-1) = 0$ | VZW von $+$ zu $-$ | Hochpunkt |
| $-1 \text{ < } x \text{ < } 4$ | $f'(x) \text{ < } 0$ | $-$ | |
| $x = 4$ | $f'(4) = 0$ | ||
| $4 \text{ < } x \text{ < } \infty$ | $f'(x) > 0$ |
(b) Fülle die Lücken in der Tabelle und zeichne einen passenden Graph $f$ mit diesen Eigenschaften.
| Stelle / Intervall | $f'(x)$ | Vorzeichen/VZW | Eigenschaft von $f$ |
|---|---|---|---|
| $-\infty \text{ < } x \text{ < } 0$ | $f'(x) \text{ < } 0$ | ||
| $x = 0$ | $f'(0) = 0$ | ||
| $0 \text{ < } x \text{ < } 2$ | $f'(x) > 0$ | ||
| $x = 2$ | $f'(0) = 0$ | ||
| $2 \text{ < } x \text{ < } 4$ | $f'(x) > 0$ | ||
| $x = 4$ | $f'(0) = 0$ | ||
| $4 \text{ < } x \text{ < } \infty$ | $f'(x) > 0$ |
Aufgabe 2
Die Abbildung zeigt Information über die Ableitungsfunktion $f'$. Die Funktion $f'$ soll nur die in der Abbildung zu sehenden Nullstellen haben.
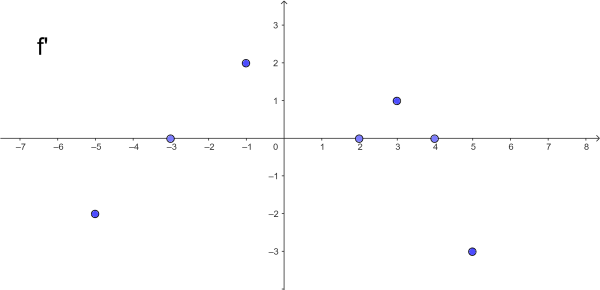
Erschließe aus dieser Information über $f'$ Eigenschaften von $f$. Begründe jeweils.
Aufgabe 3
Gegeben ist $f'$ mit
- Version A: $f'(x) = x \cdot (x-4)$
- Version B: $f'(x) = 12x^2 \cdot (x-1)$
Ziel ist es jeweils, Graph $f$ zu skizzieren.
(a) Bestimme die Nullstellen von $f'$ – die kann man hier direkt ablesen – und ermittle mit passenden Kriterien die Monotonieeigenschaften von $f$ sowie die genauen Koordinaten der Hoch-, Tief- und Sattelpunkte von $f$. Stelle die Überlegungen in einer Übersicht dar.
| Stelle / Intervall | $f'(x)$ | Vorzeichen/VZW | Eigenschaft von $f$ |
|---|---|---|---|
| $-\infty \text{ < } x \text{ < } 0$ | $f'(...) = ...$ | ||
| $x = 0$ | $f'(0) = ...$ | ||
| $-\infty \text{ < } x \text{ < } ...$ | |||
| $x = ...$ | |||
| $... \text{ < } x \text{ < } \infty$ |
(b) Zur Kontrolle soll Graph $f$ mit einem Plotter gezeichnet werden.
Bestimme einen Funktionsterm für $f(x) = ...$, so dass
$f'(x) = x \cdot (x-4) = x^2 - 4x$ (für Version A) bzw.
$f'(x) = 12x^2 \cdot (x-1) = 12x^3 - 12x^2$ (für Version B) gilt. Du musst hierzu die Funktion $f'$
aufleiten
. Gib dann die Funktion $f$ mit einem passenden Bereich in den Plotter ein.
Zum Herunterladen: plotter2.ggb
Aufgabe 4
In dieser Aufgabe betrachten wir Nullstellen von $f'$. wie beeinflusst der Verlauf von $f'$ in einer Umgebung der Nullstelle das Aussehen des Graphen von $f$?
(a) Test das Applet mit den verschiedenen Einstellmöglichkeiten.
(b) Erzeuge im Applet eine Situation, in der Graph $f'$ an einer Stelle $x$ eine Nullstelle mit einem $+/-$-Vorzeichenwechsel hat. Begründe mit Monotonieeigenschaften, dass Graph $f$ an der Stelle $x$ einen Hochpunkt haben muss.
(c) Erzeuge im Applet eine Situation, in der Graph $f'$ an einer Stelle $x$ eine Nullstelle mit einem $-/+$-Vorzeichenwechsel hat. Begründe mit Monotonieeigenschaften, dass Graph $f$ an der Stelle $x$ einen Tiefpunkt haben muss.
Anleitung für das Applet
- Im unteren Fenster kann man mit Hilfe der Schieberegler den Verlauf der Ableitungsfunktion $f'$ in der Umgebung einer Nullstelle variieren.
- Im oberen Fenster wird passend zur eingestellten Ableitungsfunktion der Graph der Ausgangsfunktion angezeigt.
- Mit dem Schieberegler $c$ kann man den Graph der Ausgangsfunktion nach oben und unten verschieben. Hiermit soll angedeutet werden, dass man die Ausgangsfunktion aus der Ableitungsfunktion nur bis auf eine additive Konstante rekonstruieren kann.
Zum Herunterladen: vzwkriterium.ggb
