o-mathe | Nullstellen von Funktionen » Übungen

Übungen – Nullstellen

Aufgabe 1

Bestimme die Nullstellen der folgenden Funktionen mit einem geeigneten rechnerischen Verfahren.

$f (x) = x^{2} - x$
$f (x) = x^{2} \cdot (2 x - 4)$
$f (x) = x^{2} + 2 x + 1$
$f (x) = x^{2} - x - 6$
$f (x) = x^{4} - 2 x^{3} + x^{2}$
$f (x) = x^{4} + x^{2}$

Kontrolliere anschließend die Ergebnisse mit dem Nullstellentool.

Zum Herunterladen: nullstellentool2.ggb

Aufgabe 2

(a) Konstruiere jeweils eine Funktion, die die angegebenen Nullstellen hat.

$x = 4$ und $x = - 2$
$x = 0$ und $x = 5$
$x = - 1$ und $x = 1$

(b) Konstruiere mindestens 3 verschiedene Funktionen, die die angegebenen Nullstellen haben.

$x = 0$
$x = 1$ und $x = 2$

Kontrolliere anschließend die Ergebnisse mit dem Nullstellentool aus Aufgabe 1.

Aufgabe 3

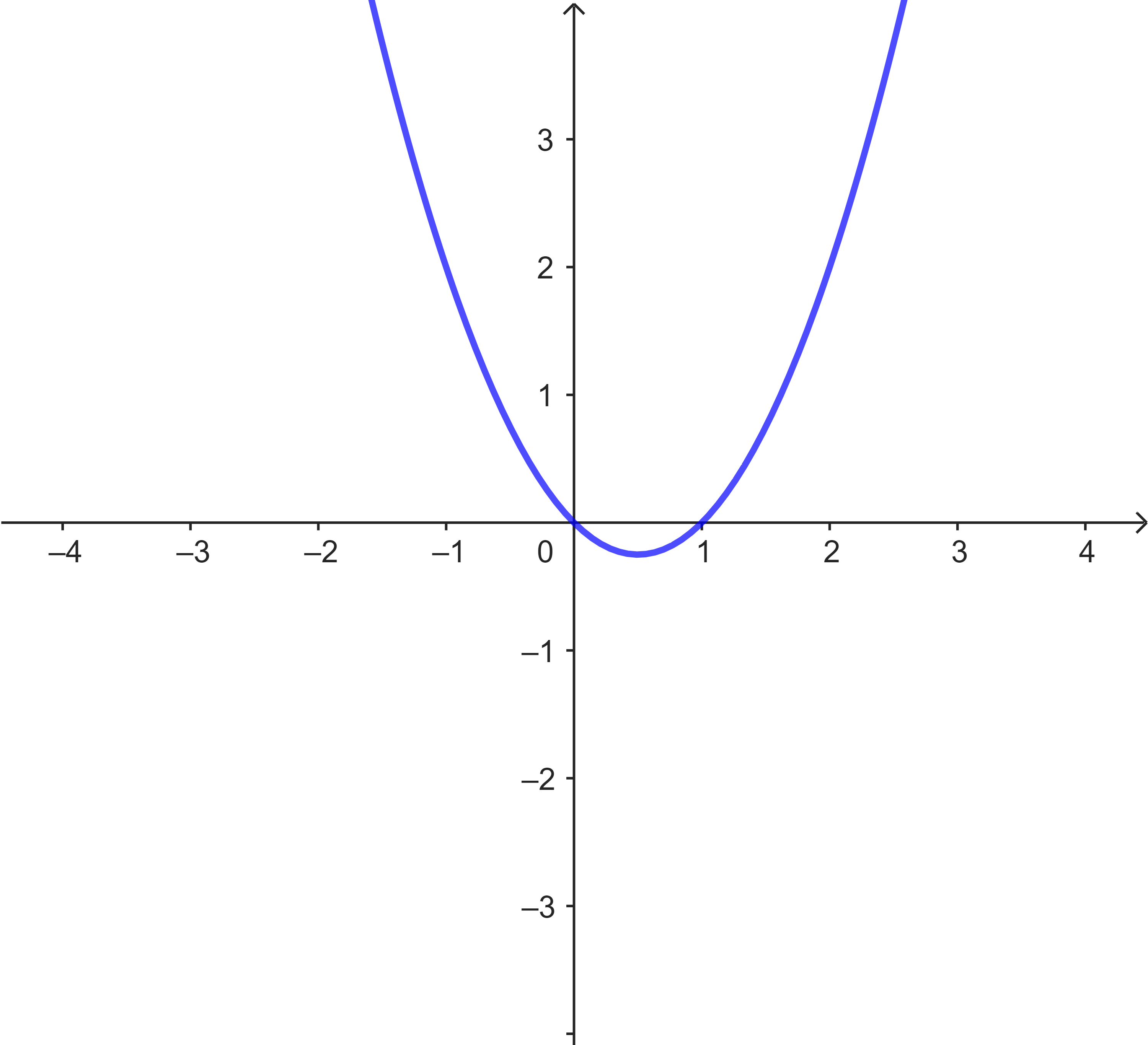
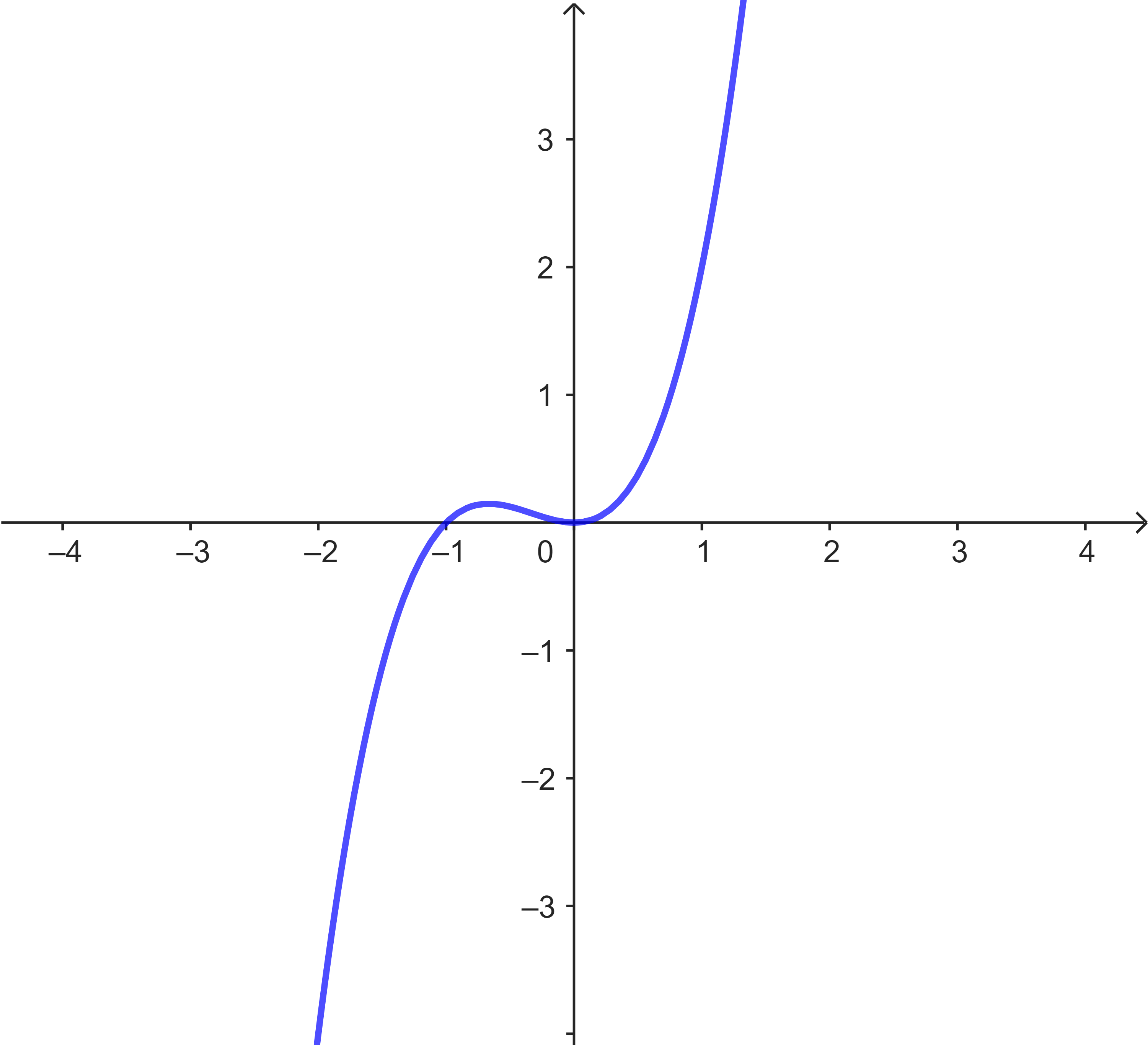
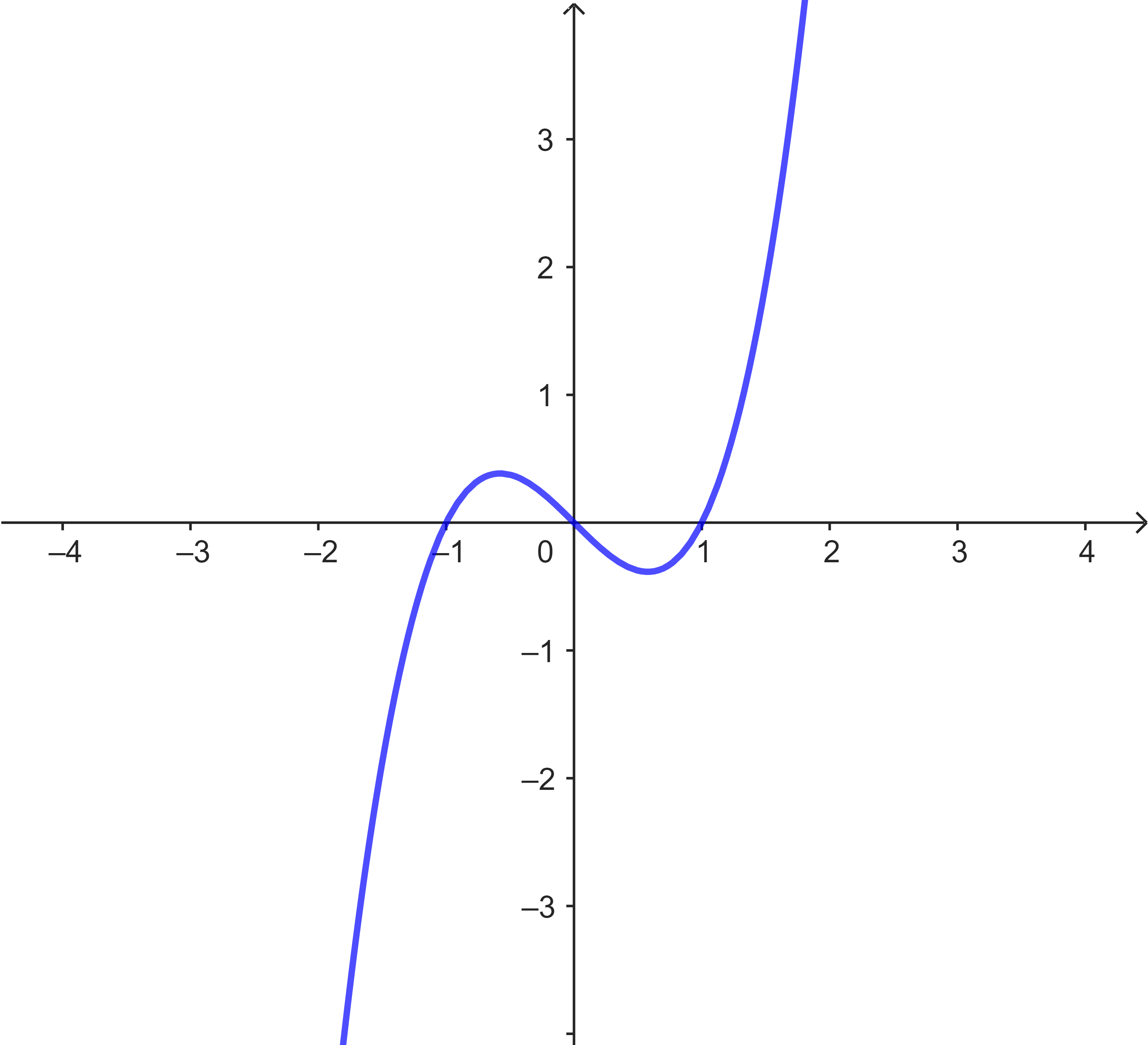
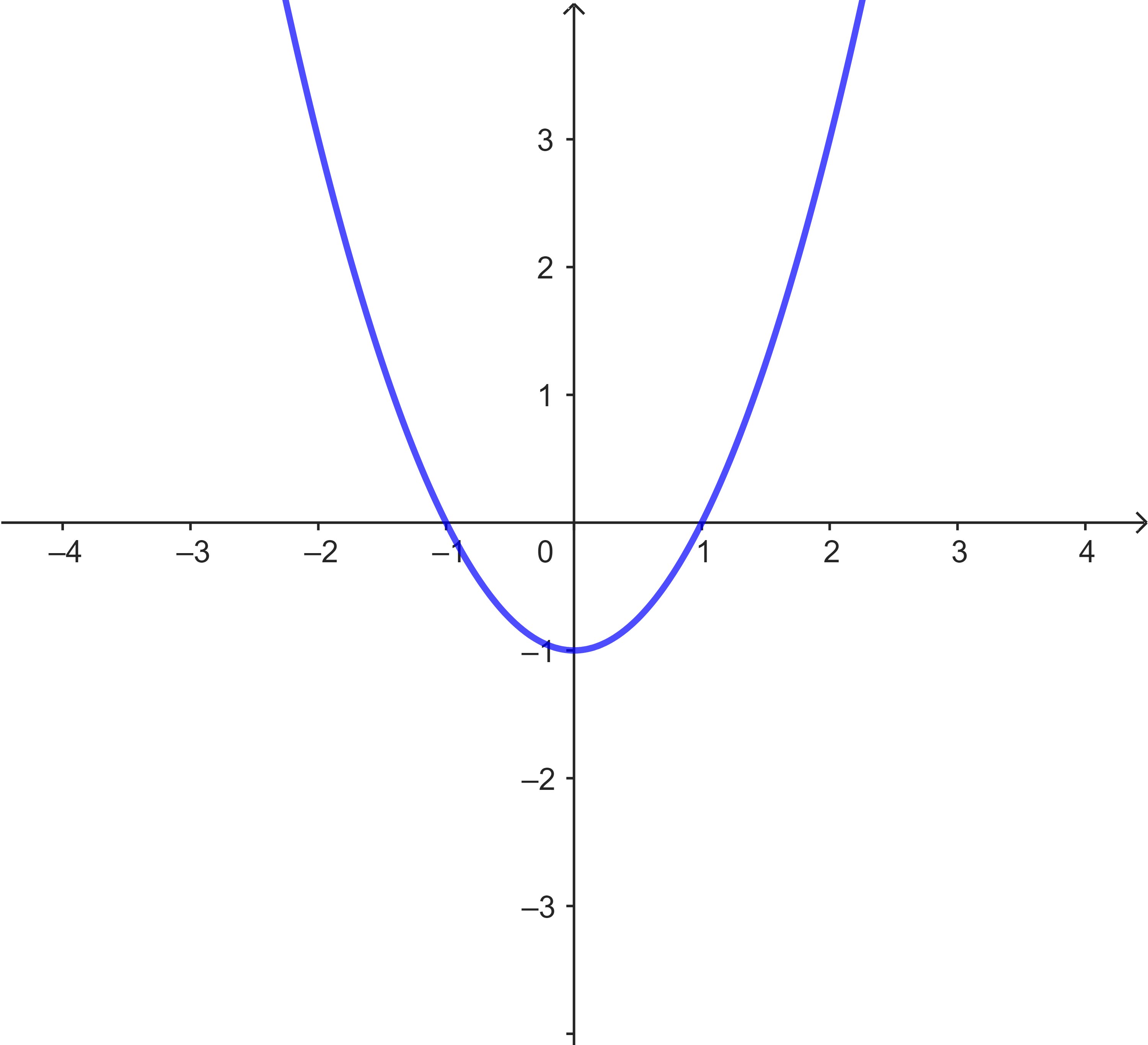
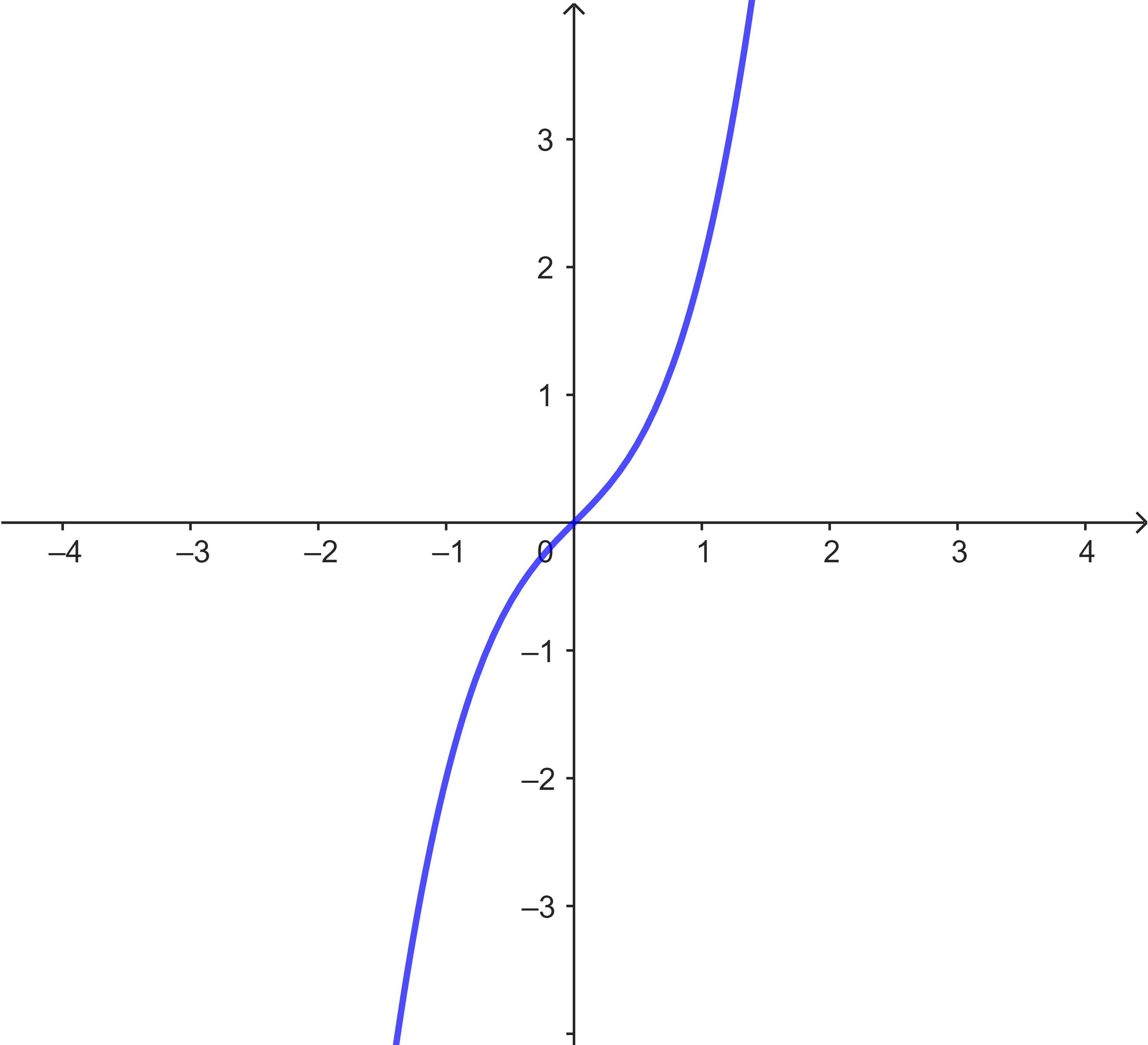
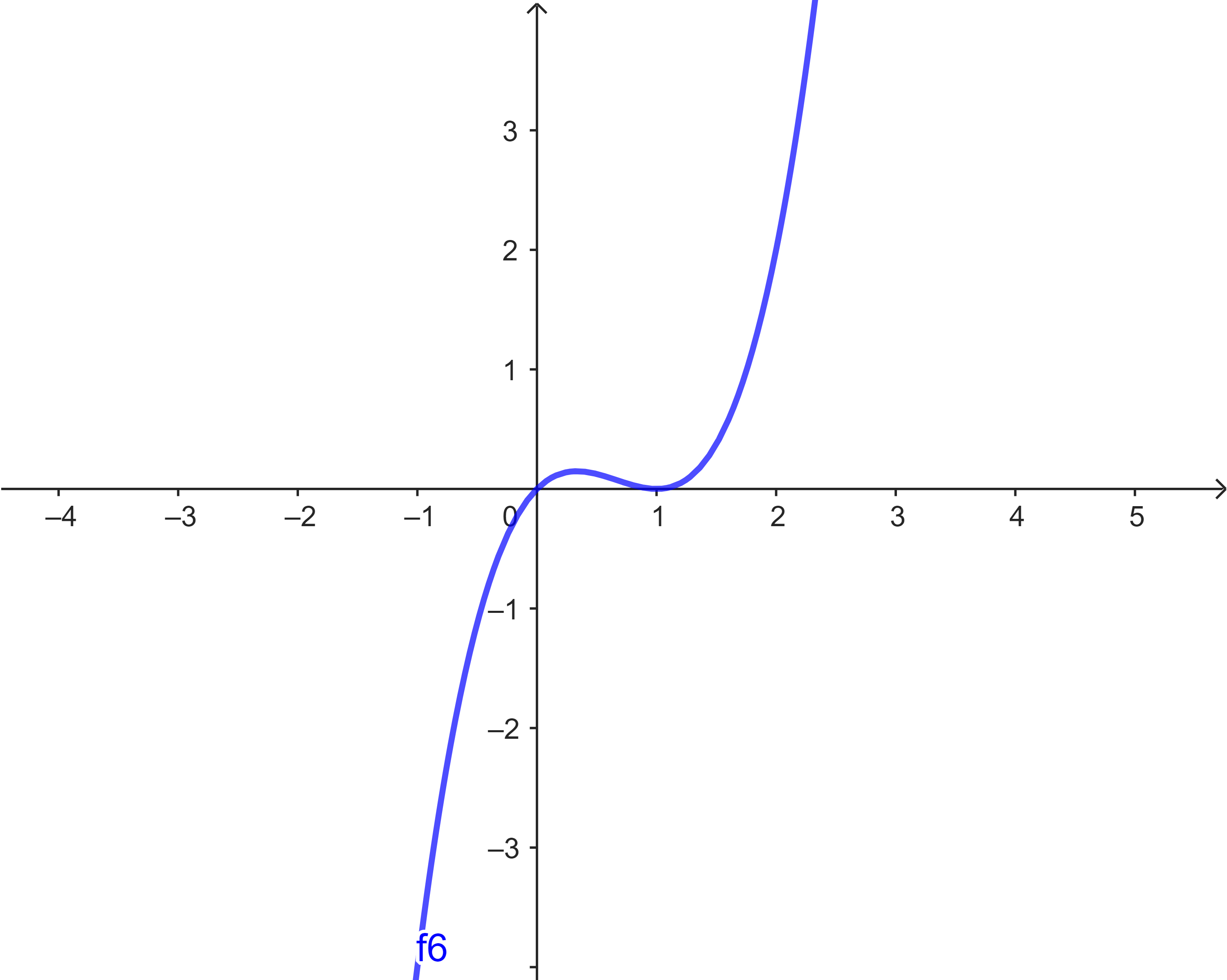
Gegeben sind hier verschiedene Funktionsgraphen (s.u.).

Ordne den Graphen die korrekten Funktionsgleichungen zu. Benutze zum Argumentieren die Nullstellen der Funktionen.

Hier die Funktionsgleichungen:

$f (x) = x^{2} - 1$
$f (x) = x^{3} - x$
$f (x) = x^{3}$
$f (x) = x^{3} + x^{2}$
$f (x) = x^{2} - x$
$f (x) = x^{3} - 2 x^{2} + x$

Graph	Nullstellen	Funktionsgleichung

Kontrolliere die Ergebnisse mit dem Nullstellentool.

Zum Herunterladen: nullstellentool2.ggb

Aufgabe 4

Wir betrachten den Fall, dass der Funktionsterm der gegebenen Funktion $f$ als Produkt aus einfachen Teiltermen dargestellt ist.

(a) Ergänze die Nullstellen in der Tabelle.

Funktion	Nullstellen
$f (x) = (x + 1) (x - 2) (x - 4)$	$x = - 1$ ; $x = 2$ ; $x = 4$
$f (x) = x (x + 4)$
$f (x) = x^{2} (x - 2) (x + 2)$
$f (x) = (x + 1)^{2} (x - 1)^{2}$
$f (x) = (x^{2} + 1) (x - 1)$
$f (x) = (x^{2} + 1) (x^{4} + 1)$
$f (x) = (2 x - 1) (- x + 2)$
$f (x) = (2 x - 2) (x + 1)^{2}$

(b) Verdeutliche zunächst mit Zahlen: Ein Produkt ergibt $0$ genau dann, wenn mindestens einer der Faktoren die $0$ ergibt.

Erläutere anschließend die folgende Herleitung der Nullstellen von $f$ mit $f (x) = (2 x - 2) (x + 1)^{2}$ .

$\begin{array}{lcl} f (x) = 0 & \Leftrightarrow & 2 x - 2 = 0 oder (x + 1)^{2} = 0 \\ \Leftrightarrow & 2 x = 2 oder x + 1 = 0 \\ \Leftrightarrow & x = 1 oder x = - 1 \end{array}$

(c) Das folge Faktorisierungstool wandelt einen Funktionsterm in ein Produkt aus einfachen Teiltermen um. Benutze es, um die Nullstellen der folgenden Funktionen zu bestimmen.

$f (x) = x^{2} - 1$
$f (x) = x^{3} - x$
$f (x) = x^{3} + 1$
$f (x) = x^{3} + x^{2}$
$f (x) = x^{2} - x$
$f (x) = x^{3} - 2 x^{2} + x$

Zum Herunterladen: faktorisierungstool.ggb

Aufgabe 5

Die Gewinne eines Unternehmens lassen sich nach Auskunft von Beratern mit der Funktion $g$ mit $g (x) = - 0.1 x^{3} + 3 x^{2} + 60 x - 800$ (vereinfacht) beschreiben. Die Variable $x$ gibt produzierte Ware in Mengeneinheiten an, der zugehörige Gewinn $g (x)$ wird in passenden Geldeinheiten angegeben.

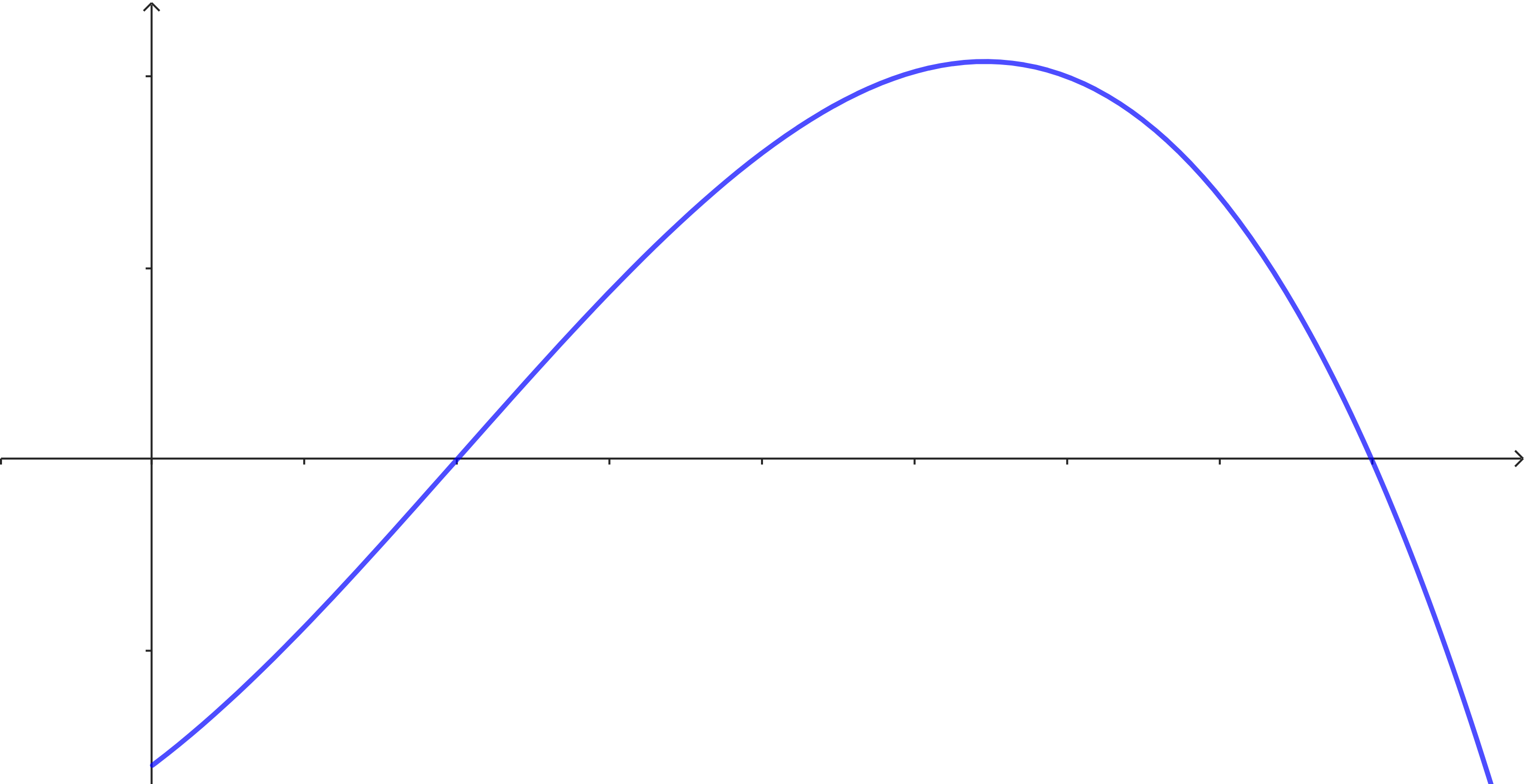
(a) Das Unternehmen möchte wissen, in welchem Bereich mit einem positiven Gewinn zu rechnen ist. Gib dem Unternehmen einen begründeten Ratschlag.

(b) Schätze mit der Grafik oben und den Daten aus (a) ab, wann der maximale Gewinn erzielt wird. Schätze diesen Gewinn auch mit der gegebenen Funktion $g$ ab.

Für Nullstellenberechnungen kannst du das Faktorisierungstool verwenden.