Lösungen zu Vorzeichenwechselkriterium
Aufgabe 1
Im folgenden Applet sind $5$ Ausgangsfunktion ($f_1, \dots, f_5$) und $3$ Ableitungsfunktion ($h_1, \dots, h_3$) vorgegeben. Ordne den $3$ Ableitungsfunktionen die passenden Ausgangsfunktionen zu. Begründe die Zuordnung mit Hilfe von Monotonieeigenschaften.
Zum Herunterladen: uebungen_monotonie1.ggb
Der Graph von $h_1$ verläuft
- im Intervall $-\infty \lt x \lt -2$ unterhalb der $x$-Achse,
- im Intervall $-2 \lt x \lt 0$ oberhalb der $x$-Achse,
- im Intervall $0 \lt x \lt 3$ unterhalb der $x$-Achse,
- im Intervall $3 \lt x \lt +\infty$ oberhalb der $x$-Achse.
Die Ausgangsfunktion von $h_1$ ist daher
- im Intervall $-\infty \lt x \lt -2$ streng monoton fallend,
- im Intervall $-2 \lt x \lt 0$ streng monoton steigend,
- im Intervall $0 \lt x \lt 3$ streng monoton fallend,
- im Intervall $3 \lt x \lt +\infty$ streng monoton steigend.
Die Ausgangsfunktion von $h_1$ ist daher die Funktion $f_4$.
Analog zeigt man: Die Ausgangsfunktion von $h_2$ ist die Funktion $f_5$ und die Ausgangsfunktion von $h_3$ ist die Funktion $f_1$.
Aufgabe 2
Gegeben ist eine Tabelle mit Eigenschaften von $f'$. Gesucht sind die zugehörigen Eigenschaften von $f$ und eine Skizze eines passenden Graphen. Beachte, dass sich alle Eigenschaften in der Tabelle auf dieselbe Funktion beziehen.
(a) Vervollständige die Tabelle und zeichne einen passenden Graph $f$ mit diesen Eigenschaften.
| Stelle / Intervall | $f'(x)$ | Vorzeichen/VZW | Eigenschaft von $f$ |
|---|---|---|---|
| $-\infty \text{ < } x \text{ < } -1$ | $f'(x) > 0$ | $+$ | $f$ streng monoton steigend |
| $x = -1$ | $f'(-1) = 0$ | VZW von $+$ zu $-$ | Hochpunkt |
| $-1 \text{ < } x \text{ < } 4$ | $f'(x) \text{ < } 0$ | $-$ | $f$ streng monoton fallend |
| $x = 4$ | $f'(4) = 0$ | VZW von $-$ zu $+$ | Tiefpunkt |
| $4 \text{ < } x \text{ < } \infty$ | $f'(x) > 0$ | $+$ | $f$ streng monoton steigend |
Graph, der diese Eigenschaften hat:
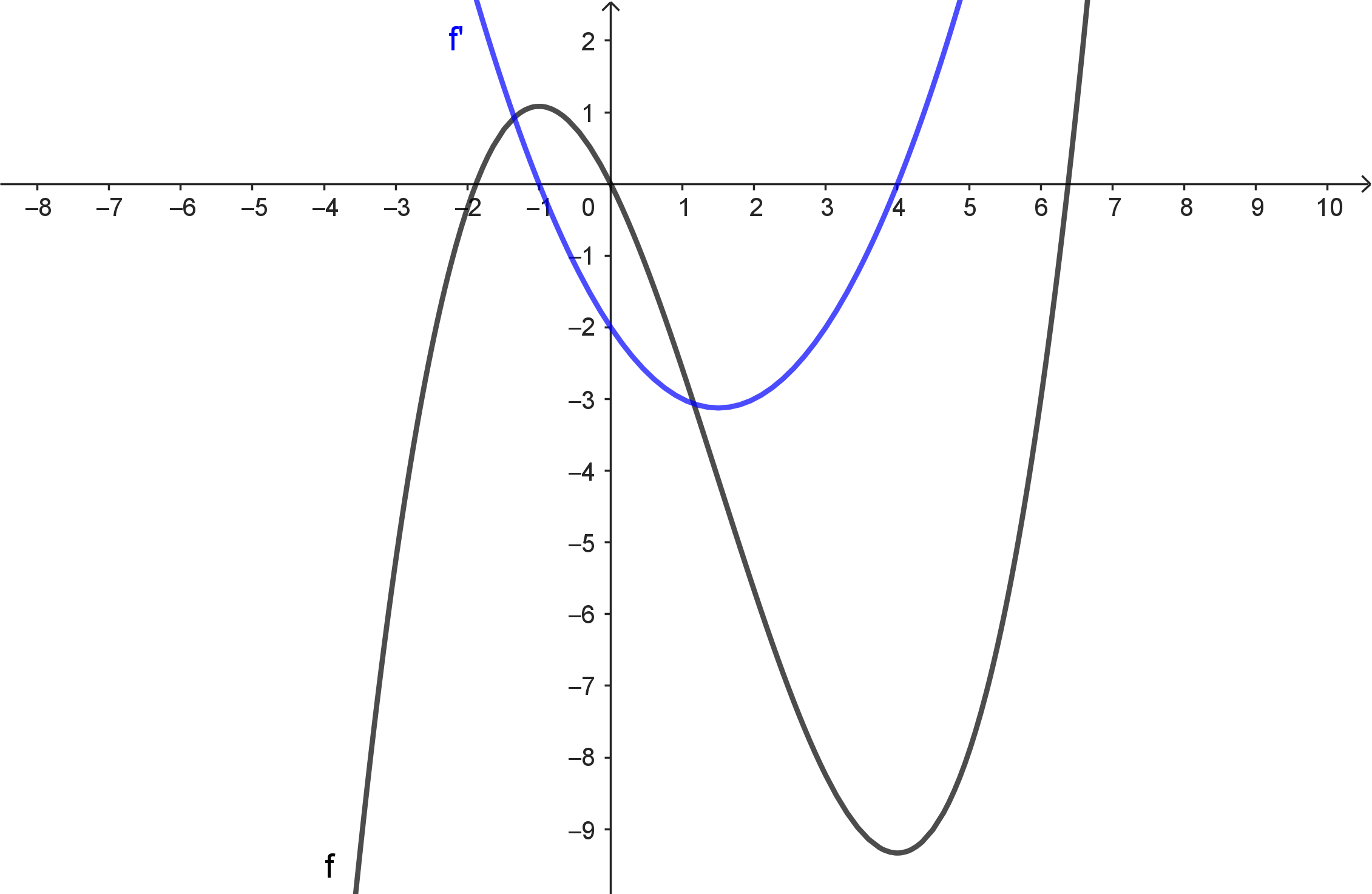
(b) Fülle die Lücken in der Tabelle und zeichne einen passenden Graph $f$ mit diesen Eigenschaften.
| Stelle / Intervall | $f'(x)$ | Vorzeichen/VZW | Eigenschaft von $f$ |
|---|---|---|---|
| $-\infty \text{ < } x \text{ < } 0$ | $f'(x) \text{ < } 0$ | $-$ | $f$ ist streng monoton fallend |
| $x = 0$ | $f'(0) = 0$ | VZW von $-$ zu $+$ | Tiefpunkt |
| $0 \text{ < } x \text{ < } 2$ | $f'(x) > 0$ | $+$ | $f$ ist streng monoton steigend |
| $x = 2$ | $f'(2) = 0$ | kein VZW | Sattelpunkt |
| $2 \text{ < } x \text{ < } 4$ | $f'(x) > 0$ | $+$ | $f$ ist streng monoton steigend |
| $x = 4$ | $f'(4) = 0$ | kein VZW | Sattelpunkt |
| $4 \text{ < } x \text{ < } \infty$ | $f'(x) > 0$ | $+$ | $f$ ist streng monoton steigend |
Graph, der diese Eigenschaften hat:
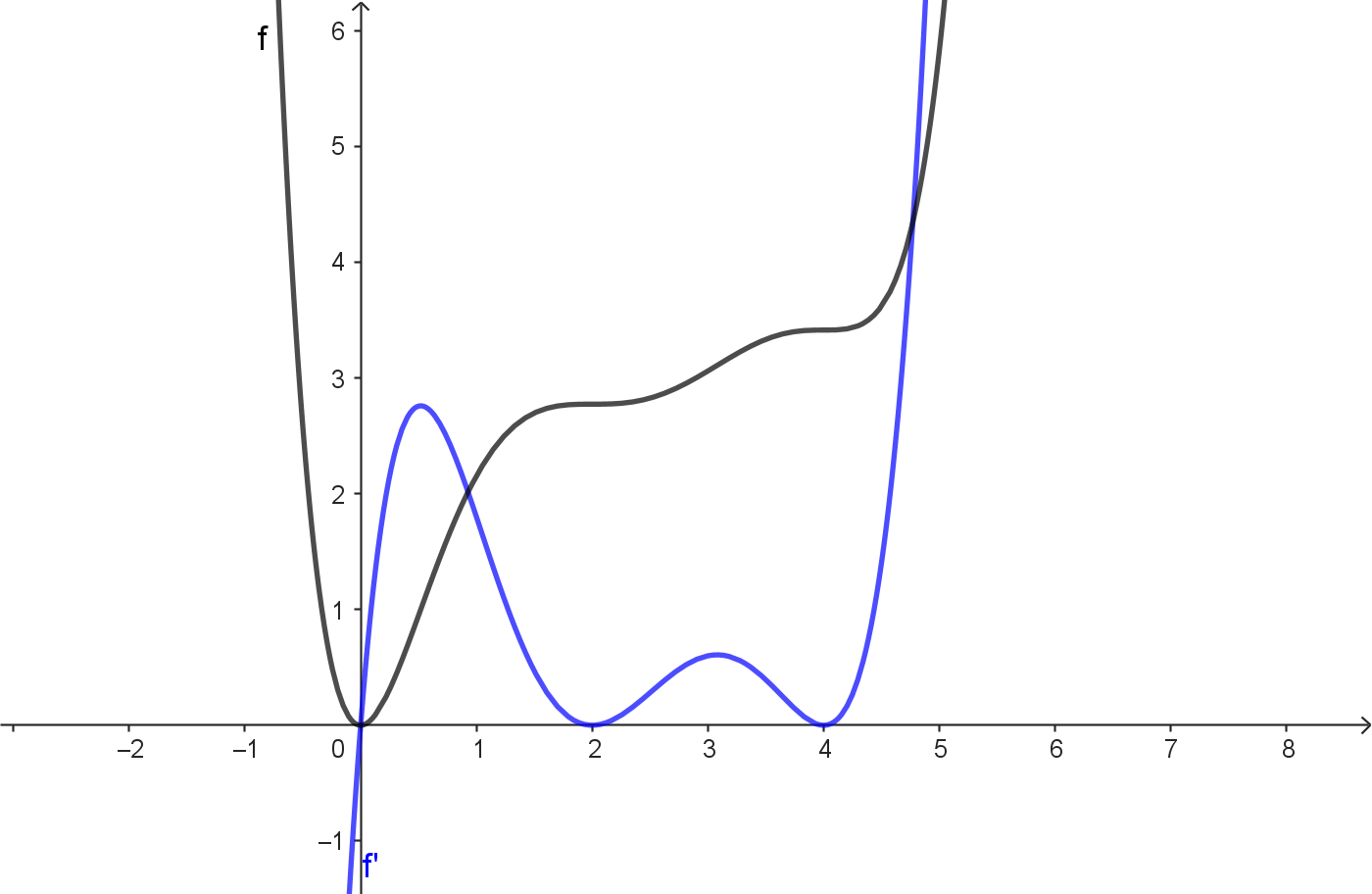
Aufgabe 3
Die Abbildung zeigt Information über die Ableitungsfunktion $f'$. Die Funktion $f'$ soll nur die in der Abbildung zu sehenden Nullstellen haben.

Erschließe aus dieser Information über $f'$ Eigenschaften von $f$. Begründe jeweils.
Aus der Abbildung kann man folgende Informationen entnehmen und dann die passenden Schlüsse ziehen.
| Stelle / Intervall | $f'(x)$ | Vorzeichen/VZW | Eigenschaft von $f$ |
|---|---|---|---|
| $-\infty \text{ < } x \text{ < } -3$ | $f'(x) \text{ < } 0$ | $-$ | $f$ ist streng monoton fallend |
| $x = 0$ | $f'(-3) = 0$ | VZW von $-$ zu $+$ | Tiefpunkt |
| $-3 \text{ < } x \text{ < } 2$ | $f'(x) > 0$ | $+$ | $f$ ist streng monoton steigend |
| $x = 2$ | $f'(2) = 0$ | kein VZW | Sattelpunkt |
| $2 \text{ < } x \text{ < } 4$ | $f'(x) > 0$ | $+$ | $f$ ist streng monoton steigend |
| $x = 4$ | $f'(4) = 0$ | kein VZW | Hochpunkt |
| $4 \text{ < } x \text{ < } \infty$ | $f'(x) \lt 0$ | $-$ | $f$ ist streng monoton fallend |
Aufgabe 4
Gegeben ist $f'$ mit
- Version A: $f'(x) = x \cdot (x-4)$
- Version B: $f'(x) = 12x^2 \cdot (x-1)$
- Version C: $f'(x) = (x+2)^2 \cdot x \cdot (x-1)$
Ziel ist es jeweils, Graph $f$ zu skizzieren.
Version A: $f'(x) = x \cdot (x-4)$
| Stelle / Intervall | $f'(x)$ | Vorzeichen/VZW | Eigenschaft von $f$ |
|---|---|---|---|
| $-\infty \text{ < } x \text{ < } 0$ | $f'(-1) = 5$ $f'(x) > 0$ |
$+$ | $f$ ist streng monoton steigend |
| $x = 0$ | $f'(0) = 0$ | VZW von $+$ zu $-$ | Hochpunkt |
| $0 \text{ < } x \text{ < } 4$ | $f'(1) = -3$ $f'(x) \lt 0$ |
$-$ | $f$ ist streng monoton steigend |
| $x = 4$ | $f'(4) = 0$ | VZW von $-$ zu $+$ | Tiefpunkt |
| $4 \text{ < } x \text{ < } \infty$ | $f'(5) = 5$ $f'(x) > 0$ |
$+$ | $f$ ist streng monoton steigend |
Durch Ausmultiplizieren erhält man $f(x) = x^2 - 4x$. Aufleiten liefert dann $f(x) = \frac{1}{3}x^3 - 2x^2 + c$ (mit einer belieben reellen Zahl $c$). Für $c = 0$ erhält man folgenden Graph:

Version B: $f'(x) = 12x^2 \cdot (x-1)$
| Stelle / Intervall | $f'(x)$ | Vorzeichen/VZW | Eigenschaft von $f$ |
|---|---|---|---|
| $-\infty \text{ < } x \text{ < } 0$ | $f'(-1) = -24$ $f'(x) \lt 0$ |
$-$ | $f$ ist streng monoton fallend |
| $x = 0$ | $f'(0) = 0$ | kein VZW | Sattelpunkt |
| $0 \text{ < } x \text{ < } 1$ | $f'(0.5) = -1.5$ $f'(x) \lt 0$ |
$-$ | $f$ ist streng monoton fallend |
| $x = 1$ | $f'(1) = 0$ | VZW von $-$ zu $+$ | Tiefpunkt |
| $1 \text{ < } x \text{ < } \infty$ | $f'(2) = 48$ $f'(x) > 0$ |
$+$ | $f$ ist streng monoton steigend |
Durch Ausmultiplizieren erhält man $f(x) = 12x^3 - 12x^2$. Aufleiten liefert dann $f(x) = 3x^4 - 4x^3 + c$ (mit einer belieben reellen Zahl $c$). Für $c = 0$ erhält man folgenden Graph:

Version C: $f'(x) = (x+2)^2 \cdot x \cdot (x-1)$
| Stelle / Intervall | $f'(x)$ | Vorzeichen/VZW | Eigenschaft von $f$ |
|---|---|---|---|
| $-\infty \text{ < } x \text{ < } -2$ | $f'(-3) = 12$ $f'(x) > 0$ |
$+$ | $f$ ist streng monoton steigend |
| $x = -2$ | $f'(-2) = 0$ | kein VZW | Sattelpunkt |
| $-2 \text{ < } x \text{ < } 0$ | $f'(-1) = 2$ $f'(x) > 0$ |
$+$ | $f$ ist streng monoton steigend |
| $x = 0$ | $f'(0) = 0$ | VZW von $+$ zu $-$ | Hochpunkt |
| $0 \text{ < } x \text{ < } 1$ | $f'(0.5) = -\frac{25}{16}$ $f'(x) \lt 0$ |
$-$ | $f$ ist streng monoton fallend |
| $x = 1$ | $f'(1) = 0$ | VZW von $-$ zu $+$ | Tiefpunkt |
| $1 \text{ < } x \text{ < } \infty$ | $f'(2) = 32$ $f'(x) > 0$ |
$+$ | $f$ ist streng monoton steigend |
Durch Ausmultiplizieren erhält man $f(x) = x^4 + 3x^3 - 4x$. Aufleiten liefert dann $f(x) = \frac{1}{5}x^5 + \frac{3}{4}x^4 - 2x^2 + c$ (mit einer belieben reellen Zahl $c$). Für $c = 0$ erhält man folgenden Graph:

Aufgabe 5
In dieser Aufgabe betrachten wir Nullstellen von $f'$. wie beeinflusst der Verlauf von $f'$ in einer Umgebung der Nullstelle das Aussehen des Graphen von $f$?
(a) Test das Applet mit den verschiedenen Einstellmöglichkeiten.
(b) Erzeuge im Applet eine Situation, in der Graph $f'$ an der Stelle $x = 0$ eine Nullstelle mit einem $+/-$-Vorzeichenwechsel hat. Begründe mit Monotonieeigenschaften, dass Graph $f$ an der Stelle $x$ einen Hochpunkt haben muss.
(c) Erzeuge im Applet eine Situation, in der Graph $f'$ an einer Stelle $x = 0$ eine Nullstelle mit einem $-/+$-Vorzeichenwechsel hat. Begründe mit Monotonieeigenschaften, dass Graph $f$ an der Stelle $x$ einen Tiefpunkt haben muss.

