Lösungen zu Übungen – Wachstumsverhalten
Aufgabe 1
Gegeben ist der Graph einer Funktion $f$, die einen komplizierteren Wachstumsprozess beschreibt.
(a) Verschiebe im Applet unter der Aufgabe die Punkte auf Graph $f$ so, dass sie eine Unterteilung in verschiedene Wachstumsphasen darstellen. Achte darauf, dass die Reihenfolge $P_1 ... P_7$ von links nach rechts erhalten bleibt.
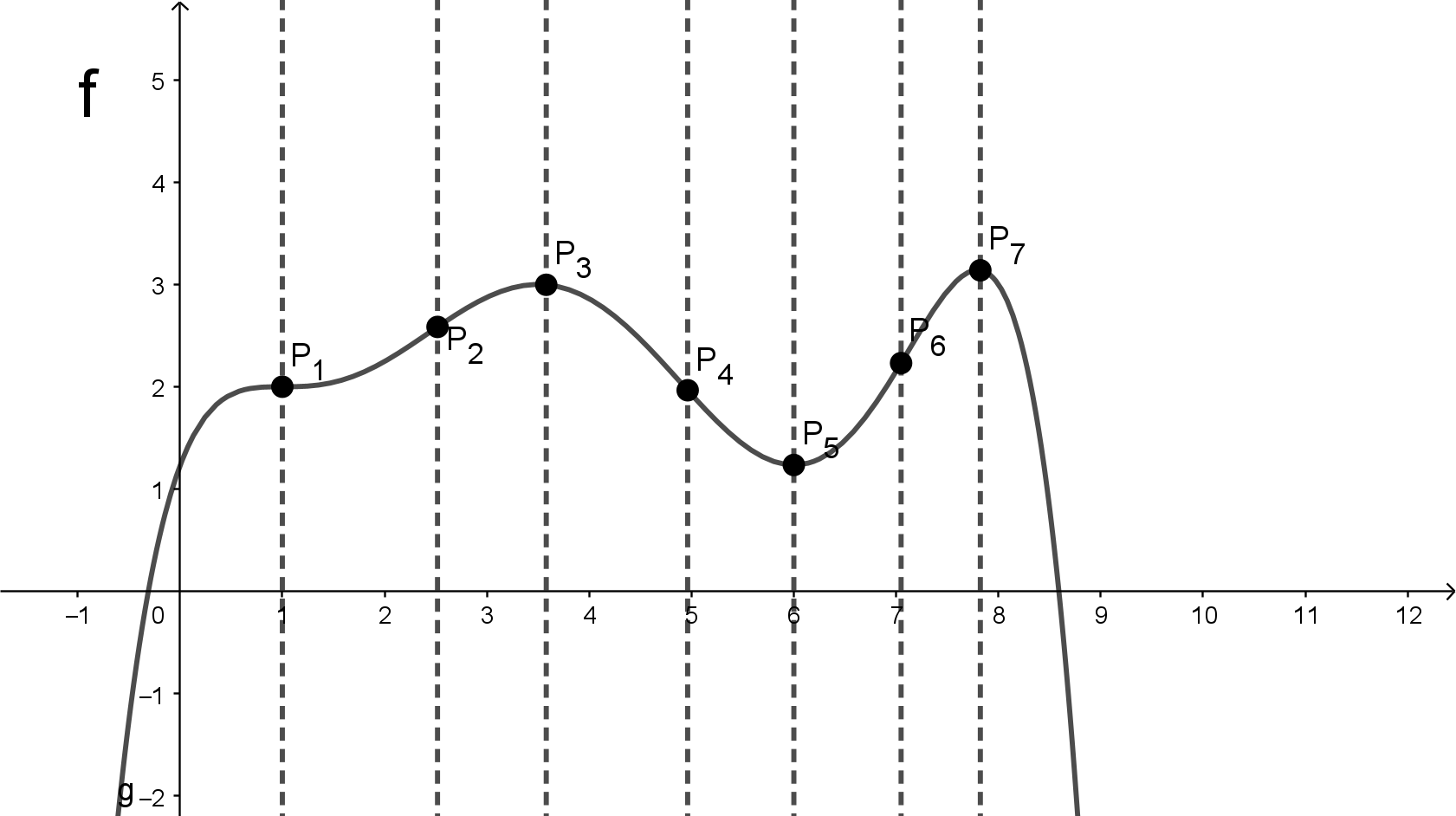
(b) Charakterisiere abschließend die verschiedenen Wachstumsphasen mit den eingeführten Fachbegriffen.
- gebremstes Wachstum im Intervall $-\infty \lt x \lt 1$
- beschleunigtes Wachstum im Intervall $1 \lt x \lt 2.5$
- gebremstes Wachstum im Intervall $2.5 \lt x \lt 3.5$
- beschleunigter Zerfall im Intervall $3.5 \lt x \lt 5$
- gebremster Zerfall im Intervall $5 \lt x \lt 6$
- beschleunigtes Wachstum im Intervall $6 \lt x \lt 7$
- gebremstes Wachstum im Intervall $7 \lt x \lt 7.7$
- beschleunigter Zerfall im Intervall $7.7 \lt x \lt \infty$
Aufgabe 2
(a) Verschiebe die Punkte auf dem Ausgangsgraph (im oberen Fenster des folgenden Applets) so, dass sie die Wendepunkte der Funktionen markieren. Zur Feinjustierung kannst du Graph $f'$ (im unteren Fenster) einblenden.
Zum Herunterladen: wendepunkteundkruemmung2loesung.ggb
(b) Ergänze die Einträge in der Tabelle.
| Stelle / Intervall | Eigenschaften von $f'$ | Eigenschaften von $f$ |
| $-\infty \text{ < } x \text{ < } 1$ | $f'$ ist streng monoton steigend | Graph $f$ ist linksgekrümmt |
| $x = 1$ | $f'$ hat einen Hochpunkt mit einem Steigungswechsel | $f$ hat einen Wendepunkt |
| $1 \text{ < } x \text{ < } 4$ | $f'$ ist streng monoton fallend | Graph $f$ ist rechtsgekrümmt |
| $x = 4$ | $f'$ hat einen Tiefpunkt mit einem Steigungswechsel | $f$ hat einen Wendepunkt |
| $4 \text{ < } x \text{ < } 7$ | $f'$ ist streng monoton steigend | Graph $f$ ist linksgekrümmt |
| $x = 7$ | $f'$ hat einen Hochpunkt mit einem Steigungswechsel | $f$ hat einen Wendepunkt |
| $7 \text{ < } x \text{ < } +\infty$ | $f'$ ist streng monoton fallend | Graph $f$ ist rechtsgekrümmt |
Aufgabe 3
Hier ist der Graph der Ableitungsfunktion $f'$ zu einem Wachstumsprozess gegeben. Welcher der vorgegebenen Graphen kommt als Ausgangsfunktion $f$ in Frage? Begründe mit Hilfe von Wachstumsarten.
Zum Herunterladen: wachstumsprozess6.ggb
| Intervall | Eigenschaften von $f'$ | Eigenschaft von $f$ |
|---|---|---|
| $-\infty \text{ < } x \text{ < } 1$ | $f'(x) \lt 0$ $f'$ ist streng monoton steigend |
gebremster Zerfall |
| $1 \text{ < } x \text{ < } 2$ | $f'(x) > 0$ $f'$ ist streng monoton steigend |
beschleunigtes Wachstum |
| $2 \text{ < } x \text{ < } 3$ | $f'(x) > 0$ $f'$ ist streng monoton fallend |
gebremstes Wachstum |
| $3 \text{ < } x \text{ < } \infty$ | $f'(x) \lt 0$ $f'$ ist streng monoton fallend |
beschleunigter Zerfall |
Die in der Übersicht aufgelisteten Eigenschaften von $f$ treffen auf Version 1 und Version 4 zu.
Aufgabe 4
Im Applet unter der Aufgabe ist der Graph der Ableitungsfunktion $f'$ zu einem Wachstumsprozess gegeben. Welche Schlüsse über den Wachstumsprozess kann man hier ziehen? Bearbeite hierzu die Aufgaben unten.
(a) An welchen Stellen hat Graph $f$ einen Hoch-, Tief- oder Sattelpunkt?
(b) In welchen Intervallen liegt beschleunigtes / gebremstes Wachstum bzw. beschleunigter / gebremster Zerfall vor?
(c) Klicke ganz links oben auf den Zeiger und wähle den Modus „Freihandskizze“ aus. Nutze den Stift, um einen möglichen Verlauf von Graph $f$ im oberen Fenster zu skizzieren. Wechsle abschließend wieder zum Bewegungsmodus und blende zur Kontrolle Graph $f$ ein.
Wachstumsprozess 1
Zum Herunterladen: wachstumsprozess5.ggb
| Stelle / Intervall | Eigenschaften von $f'$ | Eigenschaft von $f$ |
|---|---|---|
| $-\infty \text{ < } x \text{ < } 2$ | $f'(x) > 0$ $f'$ ist streng monoton fallend |
gebremstes Wachstum |
| $x = 2$ | $f'(x) = 0$ kein VZW |
$f$ hat an der Stelle $x$ einen Sattelpunkt |
| $2 \text{ < } x \text{ < } 5.5$ | $f'(x) > 0$ $f'$ ist streng monoton steigend |
beschleunigtes Wachstum |
| $5.5 \text{ < } x \text{ < } 7$ | $f'(x) > 0$ $f'$ ist streng monoton fallend |
gebremstes Wachstum |
| $x = 7$ | $f'(x) = 0$ VZW von $+$ zu $-$ |
$f$ hat an der Stelle $x$ einen Hochpunkt |
| $7 \text{ < } x \text{ < } \infty$ | $f'(x) \lt 0$ $f'$ ist streng monoton fallend |
beschleunigter Zerfall |
Wachstumsprozess 2
Zum Herunterladen: wachstumsprozess7.ggb
| Stelle / Intervall | Eigenschaften von $f'$ | Eigenschaft von $f$ |
|---|---|---|
| $-\infty \text{ < } x \text{ < } 1$ | $f'(x) > 0$ $f'$ ist streng monoton fallend |
gebremstes Wachstum |
| $x = 1$ | $f'(x) = 0$ VZW von $+$ zu $-$ |
$f$ hat an der Stelle $x$ einen Hochpunkt |
| $1 \text{ < } x \text{ < } 2.3$ | $f'(x) \lt 0$ $f'$ ist streng monoton fallend |
beschleunigter Zerfall |
| $2.3 \text{ < } x \text{ < } 4$ | $f'(x) \lt 0$ $f'$ ist streng monoton steigend |
gebremster Zerfall |
| $x = 4$ | $f'(x) = 0$ VZW von $-$ zu $+$ |
$f$ hat an der Stelle $x$ einen Tiefpunkt |
| $4 \text{ < } x \text{ < } 5.2$ | $f'(x) > 0$ $f'$ ist streng monoton steigend |
beschleunigtes Wachstum |
| $5.2 \text{ < } x \text{ < } 7$ | $f'(x) > 0$ $f'$ ist streng monoton fallend |
gebremstes Wachstum |
| $x = 7$ | $f'(x) = 0$ kein VZW |
$f$ hat an der Stelle $x$ einen Sattelpunkt |
| $7 \text{ < } x \text{ < } \infty$ | $f'(x) > 0$ $f'$ ist streng monoton fallend |
beschleunigtes Wachstum |
Wachstumsprozess 3
Zum Herunterladen: wachstumsprozess8.ggb
| Stelle / Intervall | Eigenschaften von $f'$ | Eigenschaft von $f$ |
|---|---|---|
| $-\infty \text{ < } x \text{ < } 1$ | $f'(x) > 0$ $f'$ ist streng monoton fallend |
gebremstes Wachstum |
| $x = 1$ | $f'(x) = 0$ kein VZW |
$f$ hat an der Stelle $x$ einen Sattelpunkt |
| $1 \text{ < } x \text{ < } 2.5$ | $f'(x) > 0$ $f'$ ist streng monoton steigend |
beschleunigtes wachstum |
| $2.5 \text{ < } x \text{ < } 3.5$ | $f'(x) > 0$ $f'$ ist streng monoton fallend |
gebremstes Wachstum |
| $x = 3.5$ | $f'(x) = 0$ VZW von $+$ zu $-$ |
$f$ hat an der Stelle $x$ einen Hochpunkt |
| $3.5 \text{ < } x \text{ < } 4.8$ | $f'(x) \lt 0$ $f'$ ist streng monoton fallend |
beschleunigter Zerfallsprozesse |
| $4.8 \text{ < } x \text{ < } 6$ | $f'(x) \lt 0$ $f'$ ist streng monoton steigend |
gebremste Zerfall |
| $x = 6$ | $f'(x) = 0$ VZW von $-$ zu $+$ |
$f$ hat an der Stelle $x$ einen Tiefpunkt |
| $6 \text{ < } x \text{ < } 7.1$ | $f'(x) > 0$ $f'$ ist streng monoton steigend |
beschleunigtes Wachstum |
| $7.1 \text{ < } x \text{ < } 7.8$ | $f'(x) > 0$ $f'$ ist streng monoton fallend |
gebremstes Wachstum |
| $x = 7.8$ | $f'(x) = 0$ VZW von $+$ zu $-$ |
$f$ hat an der Stelle $x$ einen Hochpunkt |
| $7.8 \text{ < } x \text{ < } \infty$ | $f'(x) \lt 0$ $f'$ ist streng monoton fallend |
beschleunigter Zerfall |

