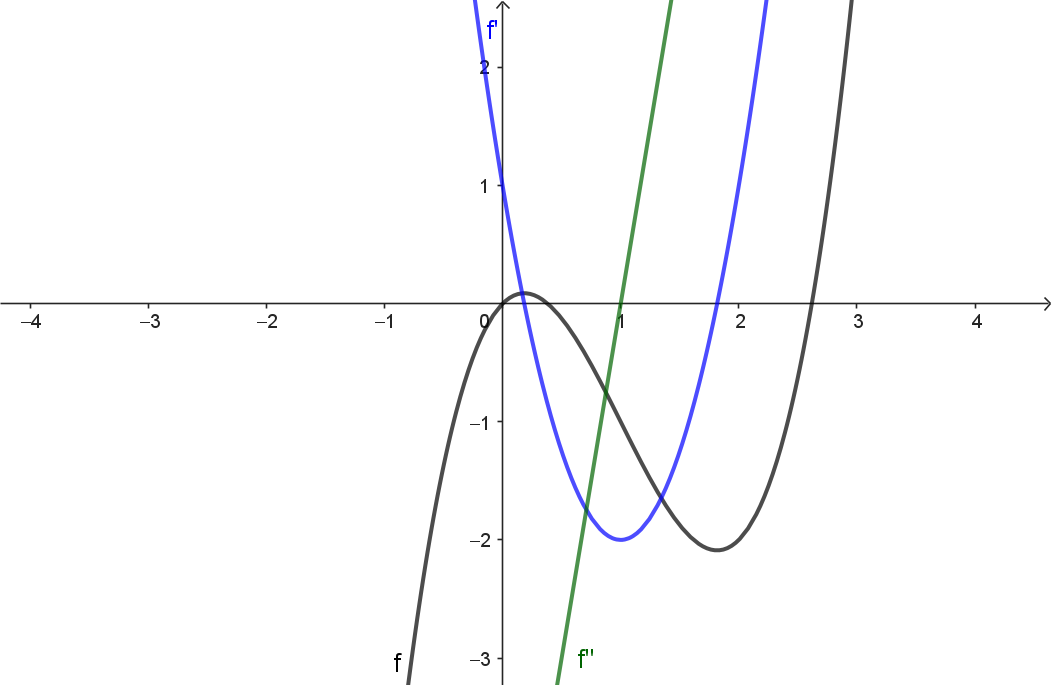
Lösungen zu Vorzeichenwechselkriterium
Aufgabe 1
Das Applet zeigt die Graphen der beiden Ableitungsfunktionen $f'$ und $f''$.
Zum Herunterladen: wendepunkte1.ggb
Ermittle mit den Eigenschaften dieser beiden Ableitungsfunktionen die Eigenschaften der Ausgangsfunktion $f$. Ergänze hierzu die Einträge in der Tabelle. Die beiden beweglichen Punkte kannst du auf der $x$-Achse verschieben, um dir zu markieren, welches Intervall du aktuell betrachtest. Überprüfe abschließend deine Ergebnisse, indem du den Graph von $f$ einblendest.
(a) Monotonie und Hoch-/Tiefpunkte
| Stelle / Intervall | $f'(x)$ | Vorzeichen/VZW | Eigenschaft von $f$ |
|---|---|---|---|
| $-\infty \text{ < } x \text{ < } -\sqrt{3}$ | $f'(x) \text{ < } 0$ | $-$ | $f$ ist streng monoton fallend |
| $x = -\sqrt{3}$ | $f'(-\sqrt{3}) = 0$ | VZW von $-$ zu $+$ | Graph $f$ hat einen Tiefpunkt |
| $-\sqrt{3} \text{ < } x \text{ < } 0$ | $f'(x) > 0$ | $+$ | $f$ ist streng monoton steigend |
| $x = 0$ | f'(0)=0 | VZW von $+$ zu $-$ | Graph $f$ hat einen Hochpunkt |
| $0 \text{ < } x \text{ < } \sqrt{3}$ | $f'(x) \lt 0$ | $-$ | $f$ ist streng monoton fallend |
| $x = \sqrt{3}$ | $f'(\sqrt{3})=0$ | VZW von $-$ zu $+$ | Graph $f$ hat einen Tiefpunkt |
| $\sqrt{3} \text{ < } x \text{ < } +\infty$ | $f'(x) > 0$ | $+$ | $f$ ist streng monoton steigend |
(b) Krümmungseigenschaften und Wendepunkte
| Stelle / Intervall | $f''(x)$ | Vorzeichen/VZW | Eigenschaft von $f$ |
|---|---|---|---|
| $-\infty \text{ < } x \text{ < } -1$ | $f''(x) > 0$ | $+$ | Graph $f$ ist linksgekrümmt |
| $x = -1$ | $f''(-1) = 0$ | VZW | Graph $f$ hat einen Wendepunkt |
| $-1 \text{ < } x \text{ < } 1$ | $f''(x) \lt 0$ | $-$ | Graph $f$ ist rechtsgekrümmt |
| $x = 1$ | $f''(1) = 0$ | VZW | Graph $f$ hat einen Wendepunkt |
| $1 \text{ < } x \text{ < } +\infty$ | $f''(x) > 0$ | $+$ | Graph $f$ ist linksgekrümmt |
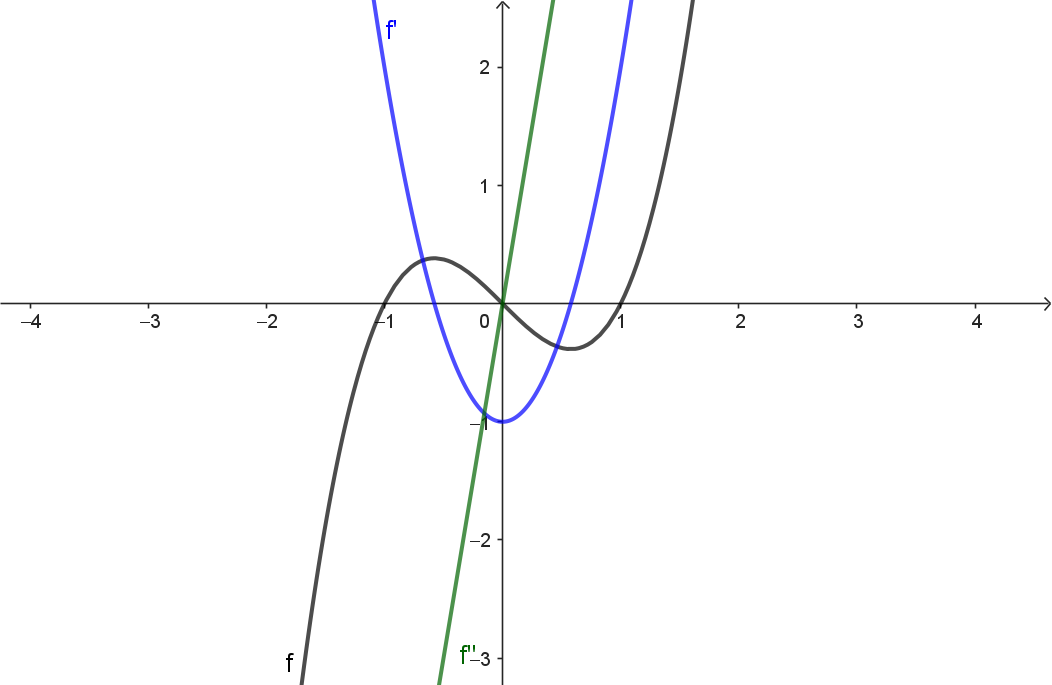
Aufgabe 2
Das Applet zeigt die Graphen der beiden Ableitungsfunktionen $f'$ und $f''$.
Zum Herunterladen: wendepunkte2.ggb
Ermittle mit den Eigenschaften dieser beiden Ableitungsfunktionen die Eigenschaften der Ausgangsfunktion $f$. Ergänze hierzu die Einträge in der Tabelle. Die beiden beweglichen Punkte kannst du auf der $x$-Achse verschieben, um dir zu markieren, welchen Intervall du aktuell betrachtest. Überprüfe abschließend deine Ergebnisse, indem du den Graph von $f$ einblendest.
(a) Monotonie und Hoch-/Tiefpunkte
| Stelle / Intervall | $f'(x)$ | Vorzeichen/VZW | Eigenschaft von $f$ |
|---|---|---|---|
| $-\infty \text{ < } x \text{ < } 0$ | $f'(x) \text{ < } 0$ | $-$ | $f$ ist streng monoton fallend |
| $x = 0$ | $f'(0) = 0$ | VZW von $-$ zu $+$ | Graph $f$ hat einen Tiefpunkt |
| $0 \text{ < } x \text{ < } +\infty$ | $f'(x) > 0$ | $+$ | $f$ ist streng monoton steigend |
(b) Krümmungseigenschaften und Wendepunkte
| Stelle / Intervall | $f''(x)$ | Vorzeichen/VZW | Eigenschaft von $f$ |
|---|---|---|---|
| $-\infty \text{ < } x \text{ < } 2$ | $f''(x) > 0$ | $+$ | Graph $f$ ist linksgekrümmt |
| $x = 2$ | $f''(2) = 0$ | VZW | Graph $f$ hat einen Wendepunkt |
| $2 \text{ < } x \text{ < } 5$ | $f''(x) \lt 0$ | $-$ | Graph $f$ ist rechtsgekrümmt |
| $x = 5$ | $f''(5) = 0$ | VZW | Graph $f$ hat einen Wendepunkt |
| $5 \text{ < } x \text{ < } +\infty$ | $f''(x) > 0$ | $+$ | Graph $f$ ist linksgekrümmt |
Aufgabe 3
Gegeben ist $f''$ mit
- Version A: $f''(x) = 6x$
- Version B: $f''(x) = 6(x+1) \cdot (x-1)$
Ziel ist es jeweils, die Wendepunkte von Graph $f$ zu bestimmen.
(a) Bestimme die Nullstellen von $f''$ – die kann man hier direkt ablesen – und ermittle mit passenden Kriterien die Krümmungseigenschaften von $f$ sowie die genauen Koordinaten der Wendepunkte von $f$. Stelle die Überlegungen in einer Übersicht dar.
(b) Zur Kontrolle soll Graph $f$ mit einem Plotter gezeichnet werden. Bestimme einen Funktionsterm für $f(x) = ...$, so dass $f''(x) = 6x$ (für Version A) bzw. $f'(x) = 6(x+1) \cdot (x-1) = 6x^2 - 6$ (für Version B) gilt. Du musst hierzu die Funktion $f''$ zweimal „aufleiten“. Gib dann die Funktion $f$ mit einem passenden Bereich in den Plotter ein.
Version A: $f''(x) = 6x$
Nullstellen von $f''$: $x = 0$
| Stelle / Intervall | $f'(x)$ | Vorzeichen/VZW | Eigenschaft von $f$ |
|---|---|---|---|
| $-\infty \text{ < } x \text{ < } 0$ | $f''(-1) = -6$ $f''(x) \lt 0$ |
$-$ | Graph $f$ ist rechtsgekrümmt |
| $x = 0$ | $f''(0) = 0$ | VZW | Wendepunkt |
| $0 \text{ < } x \text{ < } \infty$ | $f''(1) = 6$ $f''(x) > 0$ |
$+$ | Graph $f$ ist linksgekrümmt |
Aufleiten liefert $f'(x) = 3x^2 + c$ sowie $f(x) = x^3 + cx + d$ (mit belieben reellen Zahlen $c$ und $d$). Für $c = -1$ und $d = 0$ erhält man folgenden Graph:
Version B: $f''(x) = 6(x+1) \cdot (x-1)$
Nullstellen von $f''$: $x = -1$ und $x = 1$
| Stelle / Intervall | $f'(x)$ | Vorzeichen/VZW | Eigenschaft von $f$ |
|---|---|---|---|
| $-\infty \text{ < } x \text{ < } -1$ | $f''(-2) = 18$ $f''(x) > 0$ |
$+$ | Graph $f$ ist linksgekrümmt |
| $x = -1$ | $f''(-1) = 0$ | VZW | Wendepunkt |
| $1 \text{ < } x \text{ < } 1$ | $f''(0) = -6$ $f''(x) \lt 0$ |
$-$ | Graph $f$ ist rechtsgekrümmt |
| $x = 1$ | $f''(1) = 0$ | VZW | Wendepunkt |
| $1 \text{ < } x \text{ < } \infty$ | $f''(2) = 18$ $f''(x) > 0$ |
$+$ | Graph $f$ ist linksgekrümmt |
Durch Ausmultiplizieren erhält man $f(x) = 6x^2 - 6$. Aufleiten liefert $f'(x) = 3x^2 - 6x + c$ sowie $f(x) = x^3 - 3x^2 + cx + d$ (mit belieben reellen Zahlen $c$ und $d$). Für $c = 1$ und $d = 0$ erhält man folgenden Graph: