Lösungen zu Anwendungen der Kriterien
Aufgabe 1
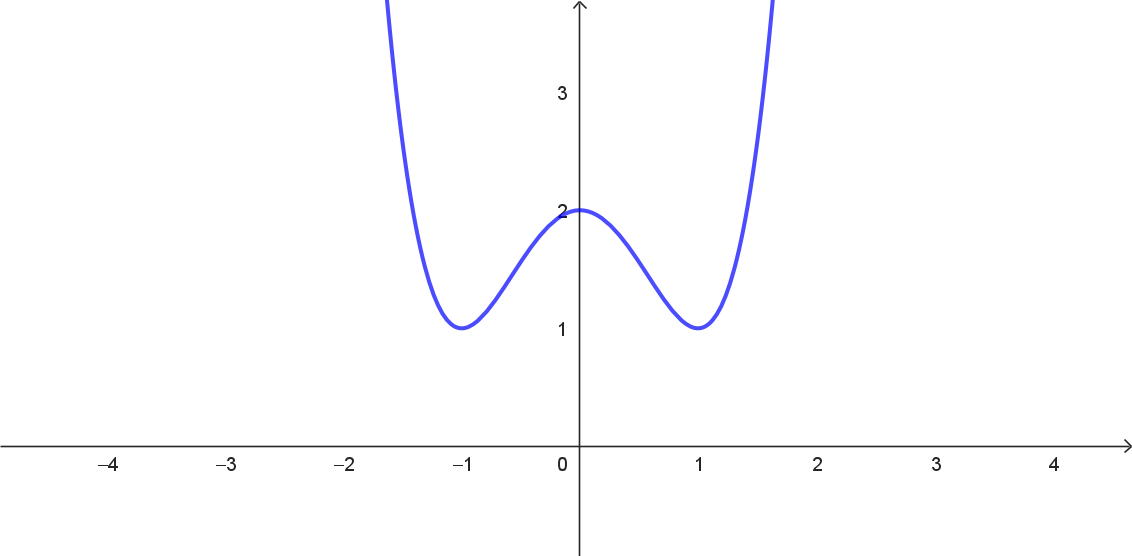
Die Abbildung zeigt den Graph der Funktion $f$ mit $f(x) = x^4 - 2 x^2 + 2$.
Im Koordinatensystem fehlt die Skalierung der Achsen. Rekonstruiere sie mit geeigneten Berechnungen.
Zum Herunterladen: skalierungbestimmen.ggb
Die Skalierung auf der $y$-Achse erhält man, indem man den Schnittpunkt von Graph $f$ mit der $y$-Achse bestimmt. Hierzu berechnet man $f(0)$. Durch Einsetzen in die gegebene Funktionsgleichung erhält man direkt $f(0) = 2$.
Um die Skalierung auf der $x$-Achse zu erhalten, bestimmt man die $x$-Koordinaten der beiden Hochpunkte. Hierzu berechnet man die Nullstellen von $f'(x)$. Man erhält die Nullstellen $-1$, $0$ und $1$.
Mit diesen Informationen kann man die Skalierung vornehmen.
Aufgabe 2
Gegeben sind die Graphen der folgenden Funktionen:
- $f(x) = -0.5 x^3 + 1.5 x^2 + 2$
- $g(x) = -0.75 x^4 + 2 x^3 + 2$
- $h(x) = 0.5 x^3 - 1.5 x^2 + 2$
Aber, welcher Graph gehört zu welcher Funktion? Löse das Problem.
Zum Herunterladen: graphenzuordnen.ggb
Eine Möglichkeit besteht darin, die kritischen Punkte (d.h. die Punkte mit der Steigung $0$) der drei Funktionen zu bestimen.
Mit dem bekannten Verfahren erhält man folgende Ergebnisse:
Kritische Punkte von Graph $f$: $(0|2)$ und $(2|4)$
Kritische Punkte von Graph $g$: $(0|2)$ und $(2|0)$
Kritische Punkte von Graph $h$: $(0|2)$ und $(2|6)$
Hieraus kann man schließen, dass Graph $f$ grün, Graph $g$ rot und Graph $h$ blau eingefärbt ist.
Aufgabe 3
Beim Kugelstoßen soll eine schwere Metallkugel (Frauen: 4kg; Männer: 7.25kg) möglichst weit gestoßen werden. Das hast du bestimmt schon einmal ausprobiert.
Die Stoßweite hängt in erster Linie von der Geschwindigkeit ab, auf die man die Kugel beim Abstoß beschleunigen kann. Hierfür braucht
man viel Kraft und eine gute Technik. Die Stoßweite hängt aber auch vom Abstoßwinkel ab. Genau diese Abhängigkeit soll hier untersucht werden.
Geklärt werden soll die Frage: Gilt beim Kugelstoßen die Faustregel: je höher, desto weiter
?
Mit dem Applet kannst du das direkt ausprobieren. Die Kugel wird hier immer mit derselben Ausgangsgeschwindigkeit von $13$ m/s gestoßen. Die Ausgangshöhe beträgt $1.80$ m (das ist die Höhe, in der die Kugel die Stoßhand verlässt).
Zum Herunterladen: kugelstossen.ggb
Für genauere Untersuchungen soll jetzt die maximale Höhe der Kugel und die erzielte Stoßweite bei verschiedenen Winkeln bestimmt werden. Im Applet ist jeweils die Funktion zur Beschreibung der Flugbahn eingeblendet. Benutze diese Funktionen bei deinen Berechnungen.
Die maximale Höhe erhält man, indem man den Hochpunkt der jeweiligen Funktion $f$ bestimmt. Hierzu muss man u.a. die Nullstelle der Ableitungsfunktion $f'$ bestimmen.
Die Stoßweite erhält man, indem man die Nullstellen der Funktion $f$ berechnet.
| Abstoßwinkel | maximale Höhe | Stoßweite |
|---|---|---|
| $35°$ | $4.58$ | $18.13$ |
| $40°$ | $5.29$ | $18.57$ |
| $45°$ | $6.03$ | $18.54$ |
| $50°$ | $6.76$ | $18.04$ |
Aufgabe 4
Gegeben ist die Funktion $f$ mit $f(x) = \displaystyle{-\frac{1}{6}x^6 + -\frac{1}{6}x^6 + \frac{104}{25}x^5 -\frac{17301}{400}x^4 + \frac{359671}{1500}x^3 -\frac{1868821}{2500}x^2 + \frac{776622}{625}x - 521}$. Gesucht sind die Hoch- und Tiefpunkte dieser Funktion.
Der Graph dieser Funktion weist eine Art Plateau auf. Nur durch das Zeichnen des Graphen ist es hier unmöglich zu entscheiden, wo die Funktion ihre Hoch- und Tiefpunkte hat.
Zum Herunterladen: graphmitplateau.ggb
Hier hilft jetzt die Theorie weiter. Nutze das Vorzeichenwechselkriterium, um die gesuchten Hoch- und Tiefpunkte der gegebenen Funktion zu bestimmen. Ein erster Schritt ist mit dem folgenden Gleichungstool bereits gemacht (warum?).
Zum Herunterladen: gleichungstool.ggb
Im Gleichungstool werden die Nullstellen von $f'$ (und damit die kritischen Stellen von $f$) angezeigt.
Man muss jetzt nur noch
herausfinden, ob an diesen Stellen Hoch-, Tief- oder Sattelpunkte vorliegen.
| Stelle / Intervall | $f'(x)$ | Vorzeichen/VZW | Eigenschaft von $f$ |
|---|---|---|---|
| $-\infty \text{ < } x \text{ < } 4$ | $f'(0) > 0$ $f'(x) > 0$ |
$+$ | $f$ ist streng monoton steigend |
| $x = 4$ | $f'(4) = 0$ | VZW von $+$ zu $-$ | Hochpunkt |
| $4 \text{ < } x \text{ < } 4.1$ | $f'(4.05) \lt 0$ $f'(x) \lt 0$ |
$-$ | $f$ ist streng monoton fallend |
| $x = 4.1$ | $f'(4.1) = 0$ | kein VZW | Sattelpunkt |
| $4.1 \text{ < } x \text{ < } 4.2$ | $f'(4.15) \lt 0$ $f'(x) \lt 0$ |
$-$ | $f$ ist streng monoton fallend |
| $x = 4.2$ | $f'(4.2) = 0$ | VZW von $-$ zu $+$ | Tiefpunkt |
| $4.2 \text{ < } x \text{ < } 4.4$ | $f'(3) > 0$ $f'(x) > 0$ |
$+$ | $f$ ist streng monoton steigend |
| $x = 4.4$ | $f'(4.4) = 0$ | VZW von $+$ zu $-$ | Hochpunkt |
| $4.4 \text{ < } x \text{ < } \infty$ | $f'(4.5) \lt 0$ $f'(x) \lt 0$ |
$-$ | $f$ ist streng monoton fallend |
Graph $f$ hat demnach Hochpunkte an den kritischen Stellen $x = 4$ und $x = 4.4$ und einen Tiefpunkt an der Stelle $x = 4.2$.
Aufgabe 5
Quadratische Funktionen sind ganzrationale Funktionen vom Grad 2. Sie lassen sich allgemein so darstellen:
$f(x) = ax^2 +bx + c$ mit reellen Zahlen $a, b, c$, wobei $a \neq 0$ vorausgesetzt wird.
Mit dem Applet unter der Aufgabe kannst du die Vorfaktoren $a, b, c$ variieren und die zugehörigen Graphen erzeugen. Beachte, dass du den Fall $a = 0$ außer Acht lassen musst.
(a) Egal, wie man die Vorfaktoren $a, b, c$ mit $a \neq 0$ wählt, man erhält immer eine Funktion mit einem Extrempunkt (Hoch- oder Tiefpunkt). Prüfe das exemplarisch nach, indem du für die Werte $a = 2$, $b = -2$ und $c = -1$ den Extrempunkt mit einem geeigneten Verfahren selbst bestimmst.
Für $a = 2$, $b = -2$ und $c = -1$ erhält man die Funktion $f(x) = 2x^2 -2x -1$. Mit $f'(x) = 4x -2$ kann man die kritische Stelle $x = 0.5$ bestimmen. Für die zweite Ableitung erhält man $f''(x) = 4x$. An der kritischen Stelle $x = 0.5$ gilt folglich $f''(0.5) = 2 > 0$. Graph $f$ hat also an der Stelle $x = 0.5$ einen Tiefpunkt.
(b) F. behauptet, dass der Extrempunkt einer ganzrationalen Funktion $f(x) = ax^2 +bx + c$ vom Grad $2$ (mit reellen Zahlen $a, b, c$, wobei $a \neq 0$) an der Stelle $x = -\frac{b}{2a}$ liegt. Überprüfe die Behauptung exemplarisch mit Hilfe des Applets.
Zum Herunterladen: extrempunkte_quadratische_funktionen.ggb
(c) Jetzt wollen wir die Aussage aus (b) auch beweisen: Zeige mit den bekannten Verfahren, dass jede Funktion $f(x) = ax^2 +bx + c$ (mit reellen Zahlen $a, b, c$, wobei $a \neq 0$) einen Extrempunkt an der Stelle $x = -\frac{b}{2a}$ hat.
Für $f(x) = ax^2 +bx + c$ erhält man die Ableitungsfunktionen $f'(x) = 2ax + b$ und $f''(x) = 2a$.
Für die Nullstelle von $f'$ erhält man $x = -\frac{b}{2a}$. Beachte, dass $a \neq 0$ vorausgesetzt ist und der Bruch so gebildet werden kann.
Da $a \neq 0$, ist $f''(x) \neq 0$. Man erhält somit an der kritischen Stelle $x = -\frac{b}{2a}$ immer einen Hoch- oder Tiefpunkt, egal wie man die Parameter $a$ und $b$ wählt.
Die Funktion $f$ hat somit einen Extrempunkt an der Stelle $x = -\frac{b}{2a}$.

