Lösungen zu Kriterium mit höheren Ableitungen
Aufgabe 1
Gegeben ist eine Tabelle mit Information über $f$, $f'$ und $f''$. Gesucht sind die Hoch- und Tiefpunkte von $f$.
| Stelle | $f(x)$ | $f'(x)$ | $f''(x)$ | Hoch-/Tiefpunkte von $f$ |
|---|---|---|---|---|
| $x = 0$ | $0$ | $0$ | $12$ | Tiefpunkt |
| $x = 2$ | $5.33$ | $0$ | $-4$ | Hochpunkt |
| $x = 3$ | $4.5$ | $0$ | $6$ | Tiefpunkt |
Aufgabe 2
Gegeben ist eine Tabelle mit Information über $f$, $f'$ und $f''$. Gesucht sind die Hoch- und Tiefpunkte von $f$. Welche Schwierigkeit tritt hier bei der Klärung auf?
| Stelle | $f(x)$ | $f'(x)$ | $f''(x)$ | Hoch-/Tiefpunkte von $f$ |
|---|---|---|---|---|
| $x = -3$ | $4.32$ | $0$ | $0$ | horizontale Tangente |
| $x = 0$ | $0$ | $0$ | $0$ | horizontale Tangente |
| $x = 2$ | $0.97$ | $0$ | $-4$ | Hochpunkt |
| $x = 3$ | $-0.68$ | $0$ | $19.44$ | Tiefpunkt |
Ohne weitere Information kann man nicht entscheiden, ob an den Stellen $x = -3$ und $x = 0$ Extrempunkte vorliegen.
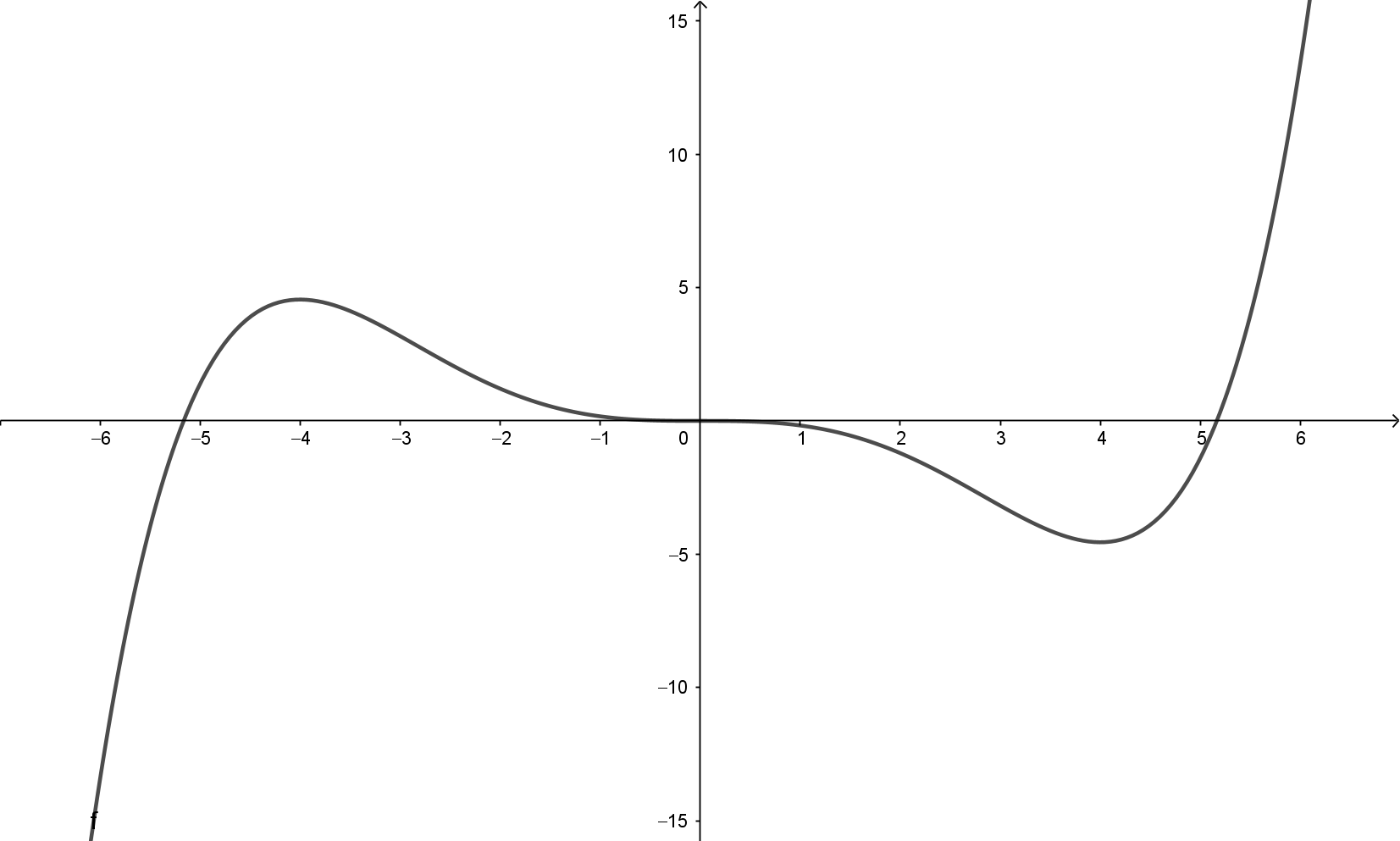
Gib zur Kontrolle den Funktionsterm $f(x) = \frac{1}{400}x^8 + \frac{1}{350}x^7 - \frac{1}{20}x^6 - \frac{9}{250}x^5 + \frac{27}{100}x^4 $ mit einem Bereich von $-3.5$ bis $3.5$ in den Plotter ein. Gleiche deine Ergebnisse mit dem Graphen ab. Diskutiere anhand dieses Beispiels die Nachteile des Kriteriums mit höheren Ableitungen.
Wenn man die Funktionsgleichung kennt und damit über sehr viel mehr an Information verfügt, kann man den Graph mit einem Plotter zeichen und sieht dann alle Extrempunkte der Funktion.
Das Beispiel zeigt, dass das Kriterium mit höheren Ableitungen nicht direkt anwendbar ist, wenn $f'(x) = 0$ und $f''(x) = 0$ gilt.
Aufgabe 3
Die Tabelle zeigt Information (gerundete Werte) über die Funktion $f$ mit $f(x) = \frac{1}{150}x^5 - \frac{8}{45} x^3$.
(a) Bestimme mit dieser Information folgende besondere Punkte von Graph $f$:
- Schnittpunkte mit der $x$-Achse und der $y$-Achse
- Hoch- und Tiefpunkte
- Sattelpunkte
Beachte, dass die Tabelle auch Information enthält, die für die Bestimmung der besonderen Punkte nicht benötigt wird. Gib jeweils genau an, wie du (mit einem passenden Kriterium) argumentierst.
| $x$ | $-5.16$ | $-4$ | $0$ | $4$ | $5.16$ |
| $f(x)$ | $0$ | $4.55$ | $0$ | $-4.55$ | $0$ |
| $f'(x)$ | $9.48$ | $0$ | $0$ | $0$ | $9.48$ |
| $f''(x)$ | $-12.85$ | $-4.27$ | $0$ | $4.27$ | $12.85$ |
Die Funktion $f$ schneidet die $x$-Achse in den Punkte $(-5.16|0)$, $(0|0)$ und $(5.16|0)$.
Die Funktion $f$ schneidet die $y$-Achse im Punkt $(0|0)$.
Die Funktion $f$ hat einen Hochpunkt mit den Koordinaten $(-4|4.55)$ und einen Tiefpunkt mit den Koordinaten $(4|-4.55)$. Die Ergebnisse erhält man mit dem Kriterium mit der zweiten Ableitung.
An der Stelle $x = 0$ hat Graph $f$ eine horizontale Tangente. Mit der zweiten Ableitung kann man nicht entscheiden, ob an dieser Stelle ein Extrempunkt oder ein Sattelpunkt vorliegt. Die Daten lassen aber aufgrund der Punktsymmetrie vermuten, dass Graph $f$ im Punkt $(0|0)$ einen Sattelpunkt hat.
(b) Skizziere mit den Ergebnissen aus (a) den Graph von $f$.
Aufgabe 4
Bestimme jeweils die Extrempunkte von $f$. Zur Kontrolle kannst du den Funktionenplotter oben benutzen.
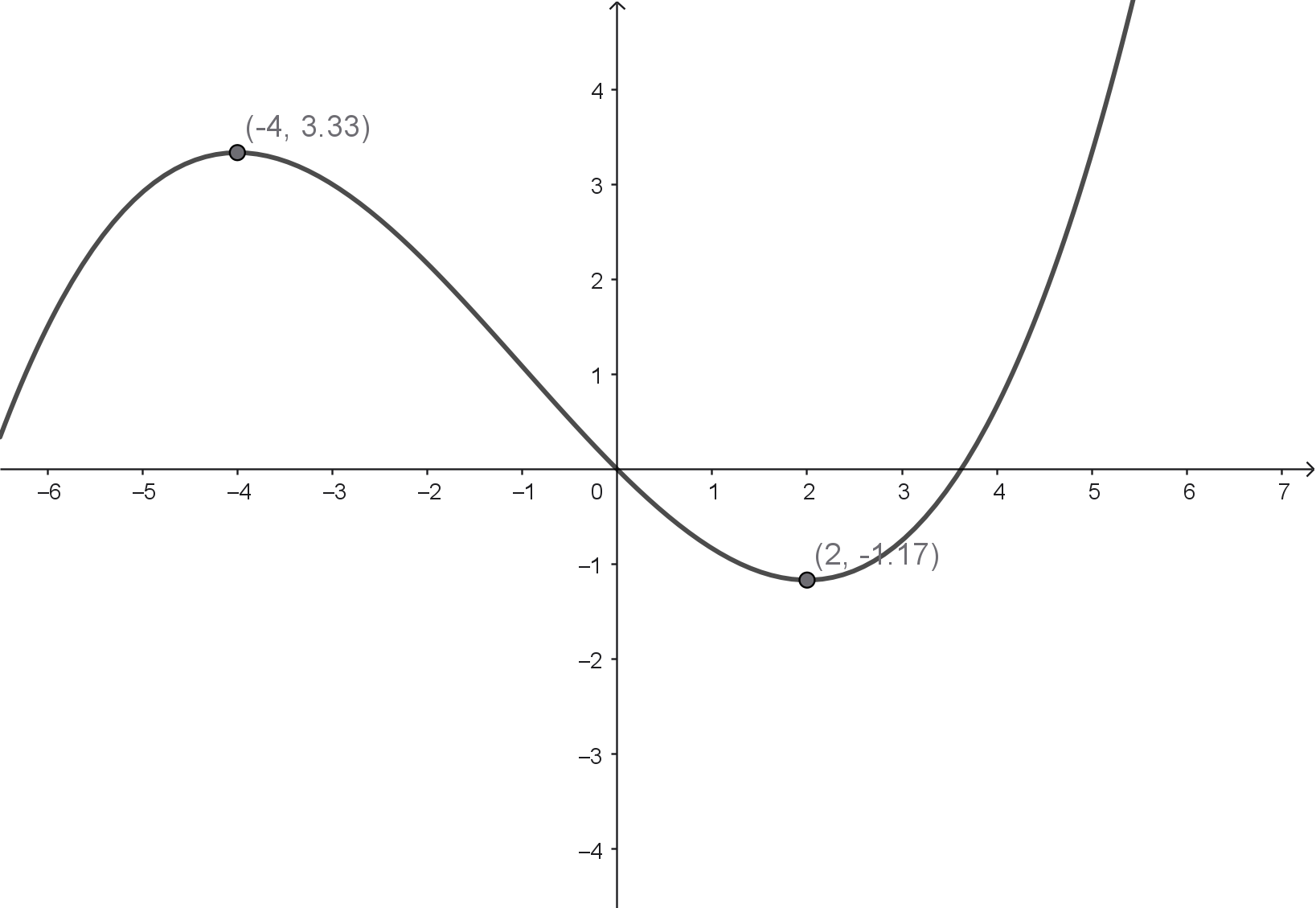
(a) $f(x) = \frac{1}{24}x^3 + \frac{1}{8}x^2 - x$
- $f'(x) = \frac{1}{8}x^2 + \frac{2}{8}x - 1 = \frac{1}{8}(x^2 + 2x - 8) = \frac{1}{8}(x - 2)(x + 4)$
- kritische Stellen für lokale Extrema: $x = -4$ und $x = 2$
- $f''(x) = \frac{1}{4}x + \frac{1}{4}$
- $f''(2) = \frac{3}{4}$; Tiefpunkt $(2|-\frac{7}{6})$
- $f''(-4) = -\frac{3}{4}$; Hochpunkt $(-4|\frac{10}{3})$
(b) $f(x) = \frac{1}{8}x^4 + \frac{1}{2}x^3 + 2$
- $f'(x) = \frac{1}{2}x^3 + \frac{3}{2}x^2 = \frac{1}{2}x^2(x + 3)$
- kritische Stellen für lokale Extrema: $x = 0$ und $x = -3$
- $f''(x) = \frac{3}{2}x^2 + 3x$
- $f''(0) = 0$; keine Aussage über Extrempunkte möglich
- $f''(-3) = \frac{9}{2}$; Tiefpunkt $(-4|-\frac{11}{8})$
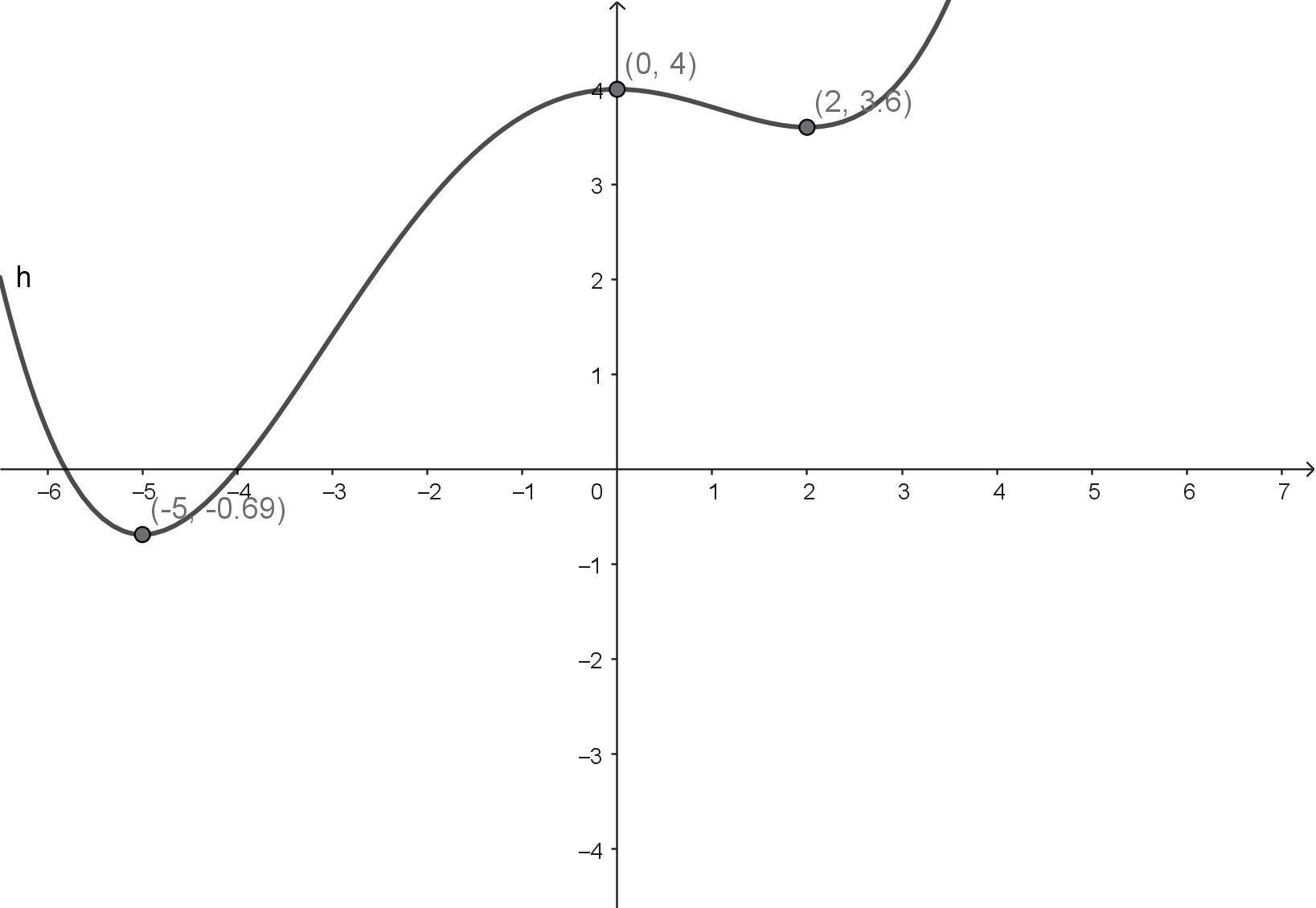
(c) $f(x) = \frac{1}{80}x^4 + \frac{1}{20}x^3 - \frac{1}{4}x^2 + 4$
- $f'(x) = \frac{1}{20}x^3 + \frac{3}{20}x^2 - \frac{1}{2}x = \frac{1}{20}(x^3 + 3x^2 - 10x) = \frac{1}{20}x(x^2 + 3x - 10) = \frac{1}{20}x(x + 5)(x - 2)$
- kritische Stellen für lokale Extrema: $x = -5$, $x = 0$ und $x = 2$
- $f''(x) = \frac{3}{20}x^2 + \frac{3}{10}x - \frac{1}{2}$
- $f''(-5) = \frac{7}{4}$; Tiefpunkt $(-5|-\frac{11}{16})$
- $f''(0) = -\frac{1}{2}$; Hochpunkt $(0|4)$
- $f''(-2) = \frac{7}{10}$; Tiefpunkt $(2|\frac{18}{5})$