Lösungen zu Kriterien mit höheren Ableitungen
Aufgabe 1
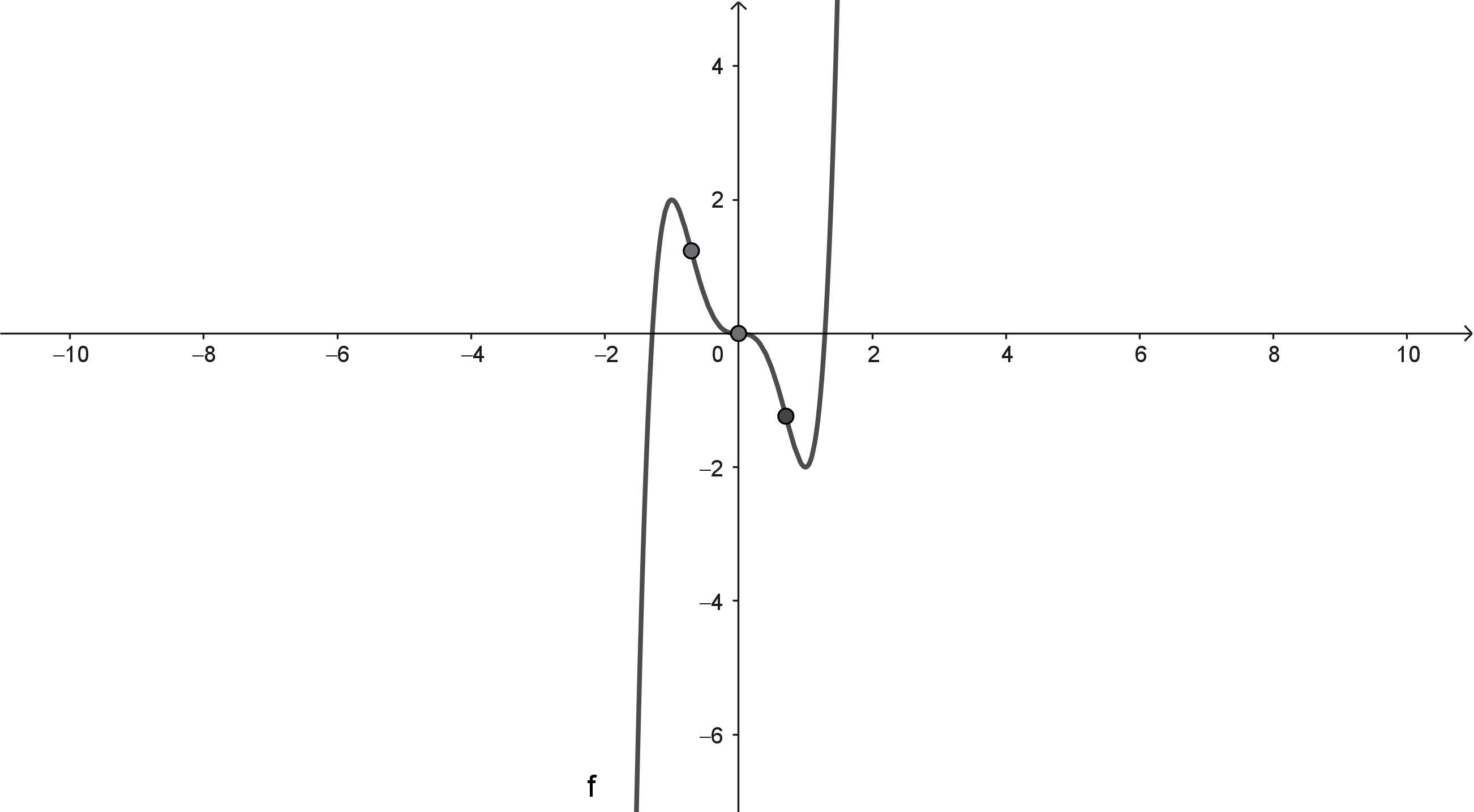
Die Tabelle zeigt Information (z.T. gerundete Werte) über die Funktion $f$ mit $f(x) = -0.0625x^4 - 0.25x^3$.
(a) Bestimme mit dieser Information folgende besondere Punkte von Graph $f$:
- Schnittpunkte mit der $x$-Achse und der $y$-Achse
- Hoch- und Tiefpunkte
- Wendepunkte / Sattelpunkte
Beachte, dass die Tabelle auch Information enthält, die für die Bestimmung der besonderen Punkte nicht benötigt wird. Gib jeweils genau an, wie du (mit einem passenden Kriterium) argumentierst.
| $x$ | $-4$ | $-3$ | $-2$ | $-1$ | $0$ | $1$ |
| $f(x)$ | $0$ | $1.69$ | $1$ | $0.19$ | $0$ | $-0.31$ |
| $f'(x)$ | $4$ | $0$ | $-1$ | $-0.5$ | $0$ | $-1$ |
| $f''(x)$ | $-6$ | $-2.25$ | $0$ | $0.75$ | $0$ | $-2.25$ |
| $f'''(x)$ | $4.5$ | $3$ | $1.5$ | $0$ | $-1.5$ | $-3$ |
Die Funktion $f$ schneidet die $x$-Achse in den Punkte $(-4|0)$ und $(0|0)$.
Die Funktion $f$ schneidet die $y$-Achse im Punkt $(0|0)$.
Die Funktion $f$ hat einen Hochpunkt mit den Koordinaten $(-3|1.69)$. Dieses Ergebnis erhält man mit dem Kriterium mit der zweiten Ableitung.
Die Funktion $f$ hat einen Wendepunkt mit den Koordinaten $(-2|1)$ und einen Sattelpunkt mit den Koordinaten $(0|0)$. Dieses Ergebnis erhält man mit dem Kriterium mit der dritten Ableitung.
(b) Skizziere mit den Ergebnissen aus (a) den Graph von $f$.
Kontrolliere mit dem Funktionenplotter. Gib hierzu den Funktionsterm $f(x) = -0.0625x^4 - 0.25x^3$ mit einem passenden Bereich (siehe Tabelle oben) in den Plotter ein.
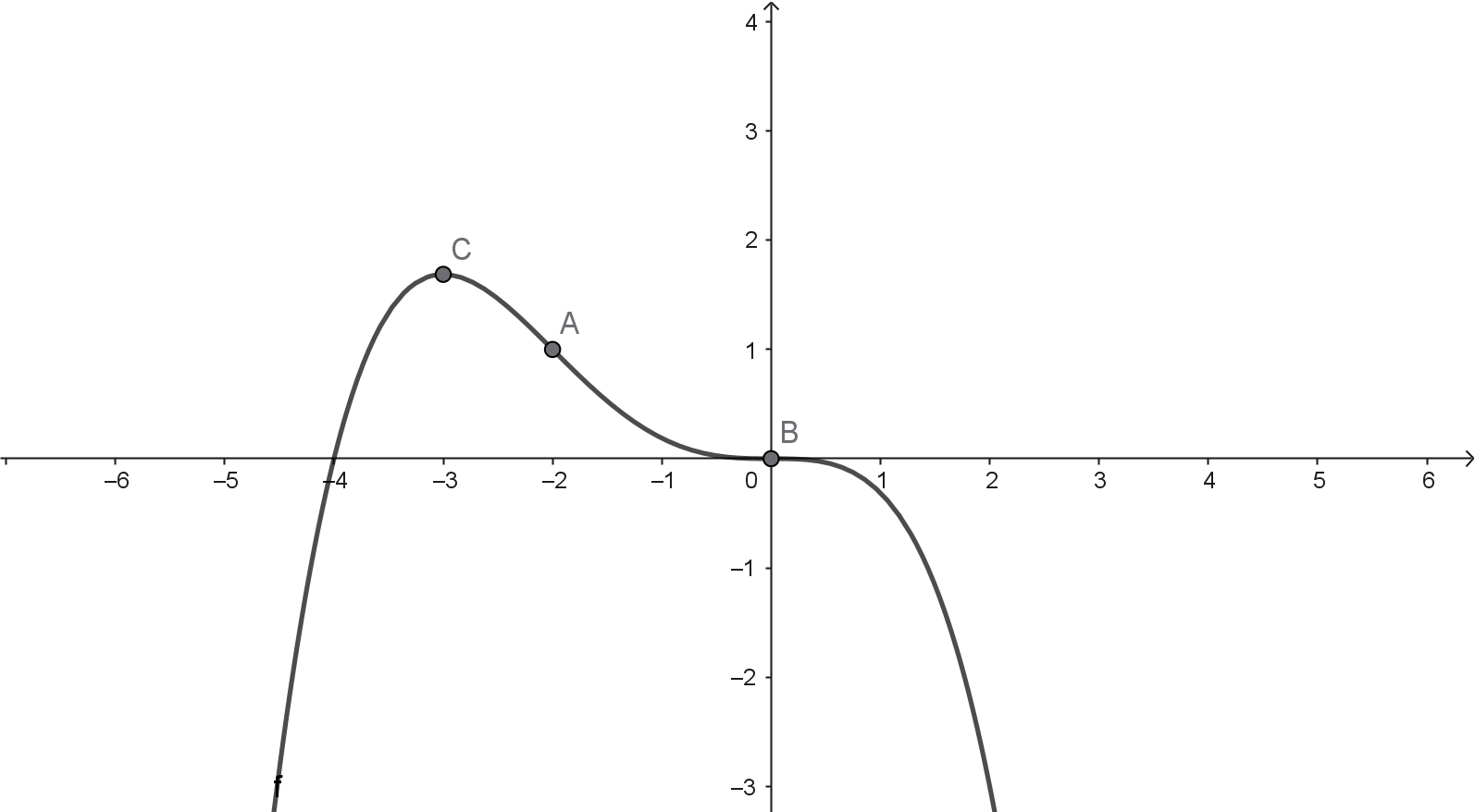
Aufgabe 2
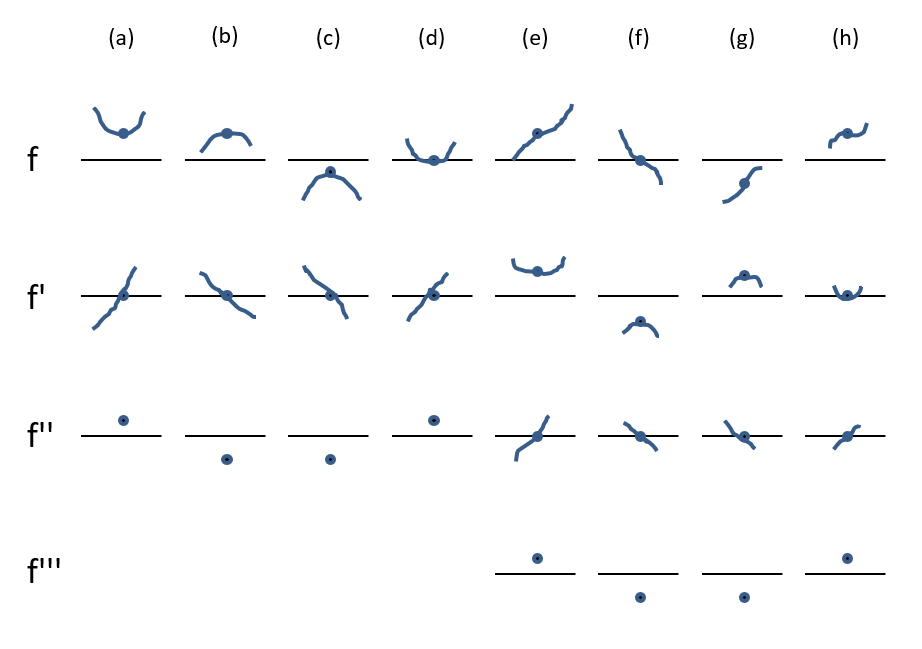
Aufgabe 3
Bestimme jeweils die Wendepunkte von $f$. Zur Kontrolle kannst du den Funktionenplotter oben benutzen.
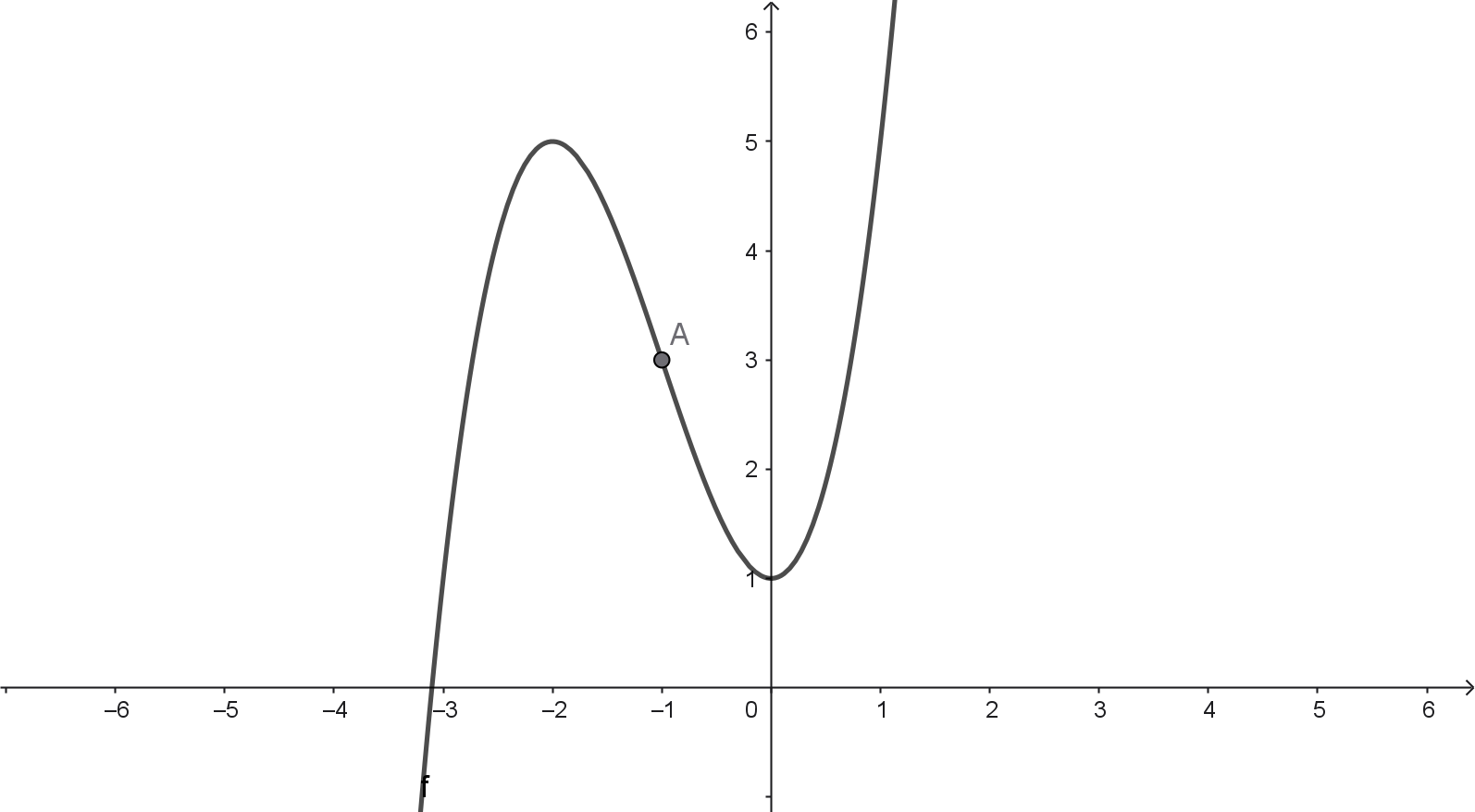
(a) $f(x) = x^3 + 3x^2 + 1$
- $f''(x) = 6x + 6 = 6(x+1)$
- kritische Stellen für Wendepunkte: $x = -1$
- $f'''(x) = 6$
- $f'''(-1) = 6 \neq 0$; Wendepunkt an der Stelle $x = -1$
- $f(-1) = 3$; Wendepunkt $(-1|3)$
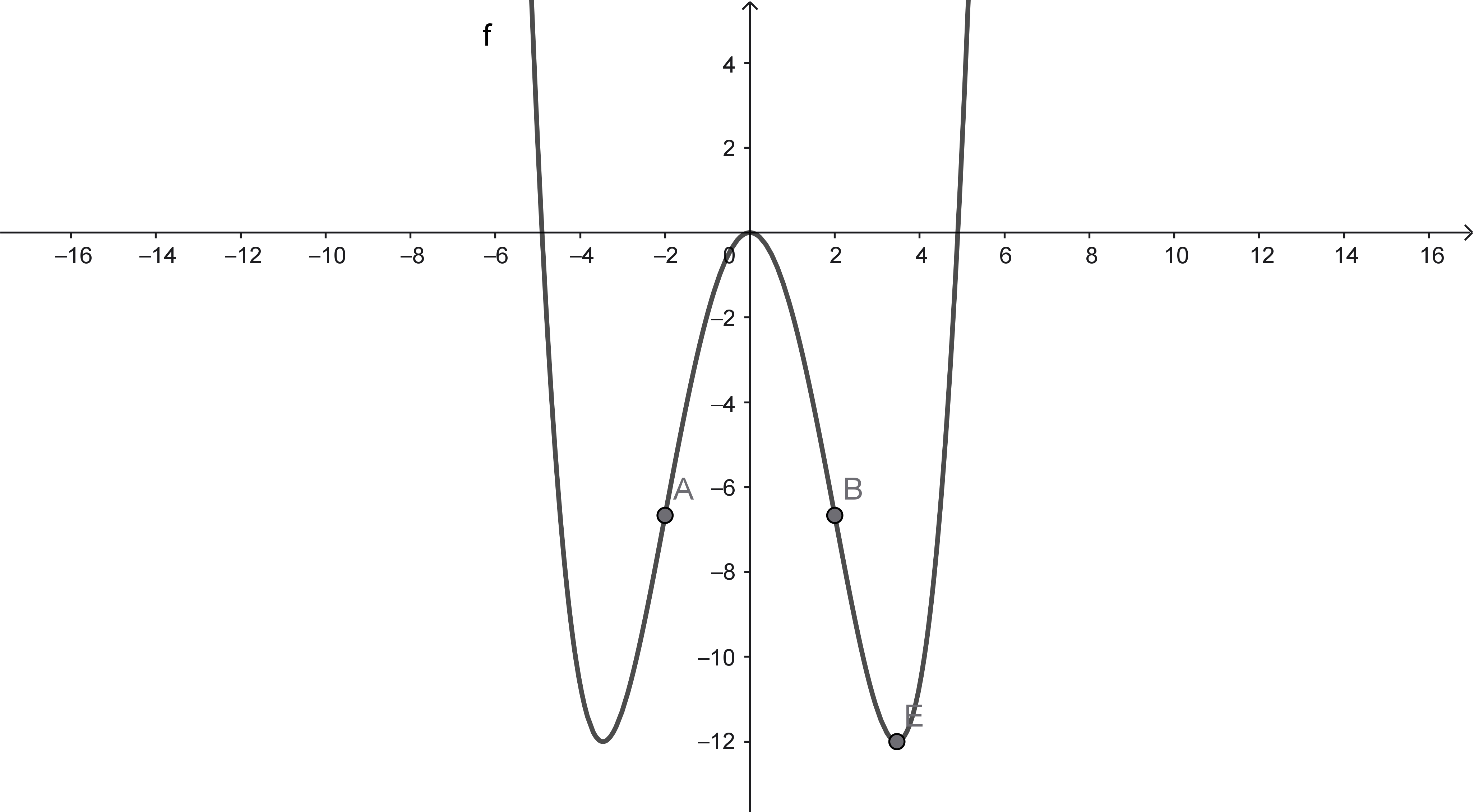
(b) $f(x) = \frac{1}{12}x^4 - 2x^2$
- $f''(x) = x^2 - 4 = (x+2)(x-1)$
- kritische Stellen für Wendepunkte: $x = -2$ und $x = 2$
- $f'''(x) = 2x$
- $f'''(-2) = -4 \neq 0$; Wendepunkt an der Stelle $x = -2$
- $f'''(2) = 4 \neq 0$; Wendepunkt an der Stelle $x = -2$
- $f(-2) = -\frac{20}{3}$; Wendepunkt $(-2|-\frac{20}{3})$
- $f(2) = -\frac{20}{3}$; Wendepunkt $(2|-\frac{20}{3})$
(c) $f(x) = 3x^5 - 5x^3$
- $f''(x) = 60x^3 - 30x = 30x(2x^2-1)$
- kritische Stellen für Wendepunkte: $x = 0$ und $x = \sqrt{0.5}$ und $x = -\sqrt{0.5}$
- $f'''(x) = 90x^2 - 30$
- $f'''(0) = -30 \neq 0$; Wendepunkt an der Stelle $x = 0$
- $f'''(\sqrt{0.5}) = 60 \neq 0$; Wendepunkt an der Stelle $x = \sqrt{0.5}$
- $f'''(-\sqrt{0.5}) = 60 \neq 0$; Wendepunkt an der Stelle $x = -\sqrt{0.5}$
- $f(-\sqrt{0.5}) = \frac{7}{8}\sqrt{0.5} \approx 1.24$; Wendepunkt $(-0.71|1.24)$
- $f(0) = 0$; Wendepunkt $(0|0)$
- $f(\sqrt{0.5}) = - \frac{7}{8}\sqrt{0.5} \approx -1.24$; Wendepunkt $(0.71|-1.24)$
- $f'(0) = 0$; Wendepunkt $(0|0)$ ist ein Sattelpunkt.