o-mathe | Bernoulli-Ketten und Trefferwahrscheinlichkeiten » Strukturierung

Strukturierung - Bernoulli-Ketten

Einstieg - den Multiple-Choice-Test analysieren

Das Zufallsexperiment „ $10$ Fragen mit je $4$ Antwortmöglichkeiten zufällig beantworten“ lässt mit Hilfe eines Baumdiagramms beschreiben:

Zum Herunterladen: struktur_bernoullikette.ggb

Aufgabe 1

Erläutere folgende Aussagen anhand des Applets:

Beim Zufallsexperiment „ $10$ Fragen mit je $4$ Antwortmöglichkeiten zufällig beantworten“ handelt es sich um ein mehrstufiges Zufallsexperiment mit $10$ Stufen (im Applet sind nur die ersten drei zu sehen).
In jeder Stufe findet das gleiche Teilexperiment statt.
Jedes Teilexperiment hat genau $2$ Ergebnisse, die als Treffer (kurz: T) und Niete (kurz: N) bezeichnet werden.
Die Wahrscheinlichkeit für einen Treffer beträgt (in jeder Stufe) $p = 0.25$ , die für eine Niete $q = 1 - p = 0.75$ .

Aufgabe 2

Zur Beschreibung solcher Zufallsexperimente werden die folgenden Fachbegriffe und Bezeichnungen verwendet:

Ein Bernoulli-Experiment ist ein Zufallsexperiment mit genau zwei Ergebnissen. Die Ergebnisse werden oft als Treffer (kurz $T$ ) und Niete (kurz $N$ ) bezeichnet. Die zugehörigen Wahrscheinlichkeiten werden Trefferwahrscheinlichkeit (kurz $p$ ) und Nietenwahrscheinlichkeit (kurz $q = 1 - p$ ) genannt.

Ein mehrstufiges Zufallsexperiment, das aus $n$ unabhängigen Wiederholungen desselben Bernoulli-Experiments besteht, wird Bernoulli-Kette der Länge $n$ (oder n-stufiges Bernoulli-Experiment) genannt.

Ergänze mit Hilfe der eingeführten Begriffe und Bezeichnungen die folgende Charakterisierung:

Beim Zufallsexperiment „ $10$ Fragen mit je $4$ Antwortmöglichkeiten zufällig beantworten“ handelt es sich um eine Bernoulli-Kette der Länge $n = \dots$ mit der Trefferwahrscheinlichkeit $p = \dots$ .

Erarbeitung - Wahrscheinlichkeiten bei Bernoulli-Ketten bestimmen

Bei Benoulli-Ketten ist folgende Frage interessant:

Leitfrage

Wie wahrscheinlich ist es, bei einer Bernoulli-Kette der Länge $n$ genau $k$ Treffer zu erzielen?

Mit der Zufallsgröße $X$ erfassen wir die Anzahl der Treffer bei einer Bernoulli-Kette. $X$ ordnet also jeder Folge aus Treffern und Nieten die Anzahl der darin vorkommenden Treffern zu.

Beispiel: $X : N N N T N N N N T N \to 2$

Ein Ereignis wie z. B. „genau 2 Treffer“ kann dann mit Hilfe der Zufallsgröße $X$ in der Form $X = 2$ beschrieben werden. Gesucht ist im Folgenden die Wahrscheinlichkeit $P (X = k)$ bei einer Bernoulli-Kette der Länge $n$ , wobei $k$ die Anzahl der Treffer angibt.

Zum Herunterladen: wahrscheinlichkeiten_bernoullikette.ggb

Aufgabe 3

Im Applet ist zu Beginn die folgende Formel zu sehen:

$P (X = 2) = (\binom{10}{2}) \cdot {0.25}^{2} \cdot {0.75}^{8}$

Erkläre die Bestandteile dieser Formel und wie sie erhalten werden.

Aufgabe 4

Betrachte das Ereignis $X = k$ für eine beliebige Bernoulli-Kette der Länge $n$ mit Trefferwahrscheinlichkeit $p$ . Beschreibe die zugehörige Wahrscheinlichkeit mit einer verallgemeinerten Formel:

$P (X = k) = \dots$

Diese Formel wird auch Formel von Bernoulli genannt.

Vertiefung - die Formel von Bernoulli anwenden

Betrachte folgende Situationen:

Zufallsexperiment: einen Multiple-Choice-Test mit 8 Fragen und je 3 Antwortmöglichkeiten durch Raten ausführen (Treffer: die richtige Antwortmöglichkeit ankreuzen)
Gesucht: die Wahrscheinlichkeit für $4$ Treffer
Zufallsexperiment: eine Münze 5-mal werfen (Treffer: es fällt Kopf)
Gesucht: die Wahrscheinlichkeit für $3$ Treffer
Zufallsexperiment: einen Würfel 12-mal werfen (Treffer: es fällt eine $6$ )
Gesucht: die Wahrscheinlichkeit für $2$ Treffer

Aufgabe 5

Beschreibe die Zufallsexperimente zunächst als Bernoulli-Ketten. Bestimme dann die gesuchten Wahrscheinlichkeiten.

💡 Tipp 1

Bediene dich aus den folgenden Fachbegriffen: Zufallsexperiment, Stufen, Trefferanzahl, Trefferwahrscheinlichkeit.

💡 Tipp 2

Nutze folgende Formulierung: "Das Zufallsexperiment hat ... Stufen. Jede Stufe enstpricht ... Die gefragte Trefferanzahl ist ... und die Trefferwahrscheinlichkeit beträgt ..."

🚀 Zusatzaufgabe für Schnellere

Nenne eine Bedingung, unter der die 2. Situation nicht durch eine Bernoulli-Kette beschrieben werden könnte. Erkläre, warum eine gezinkte Münze immer noch ein Bernoulli-Experiment ergibt.

Aufgabe 6

Gib selbst (mindestens 3) weitere Beispiele für Bernoulli-Ketten an. Bestimme jeweils eine Wahrscheinlichkeit mit der Formel von Bernoulli.

Aufgabe 7

Jan hat die folgende Rechnung notiert: $P (X = 3) = (\binom{4}{3}) \cdot 0, 3^{3} \cdot 0, 7^{1},$ wobei $X$ die Trefferanzahl bei einer Bernoulli-Kette angibt.

(a) Erläutere anhand des Beispiels die Bedeutung des Binomialkoeffizienten $(\binom{4}{3})$ . Markiere die entsprechenden Pfade im Baumdiagramm (T bedeutet Treffer, N bedeutet Niete):

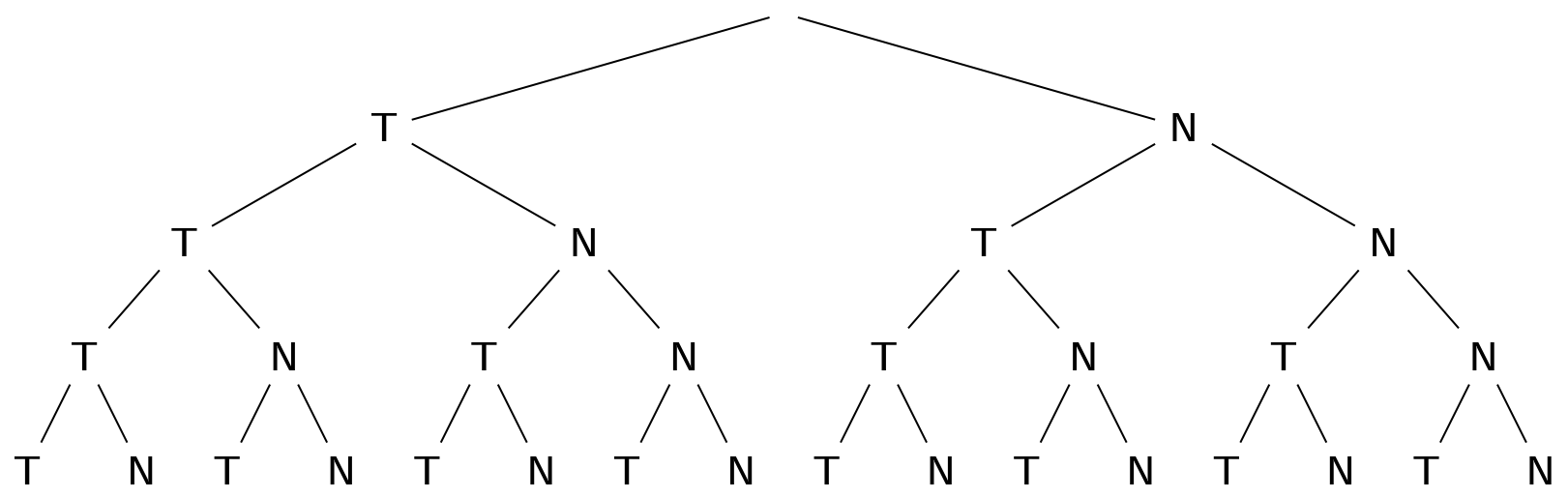
(b) Erläutere die Bedeutung der anderen beiden Faktoren $0, 3^{3}$ und $0, 7^{1}$ . Warum werden sie multipliziert?