Übungen - Binomialverteilung
Aufgabe 1
Gegeben sind Histogramme (a) bis (e) zu verschiedenen Binomialverteilungen:
| Histogramm | Parameter | Berechnungsformel der Binomialverteilung | |
| (a) | 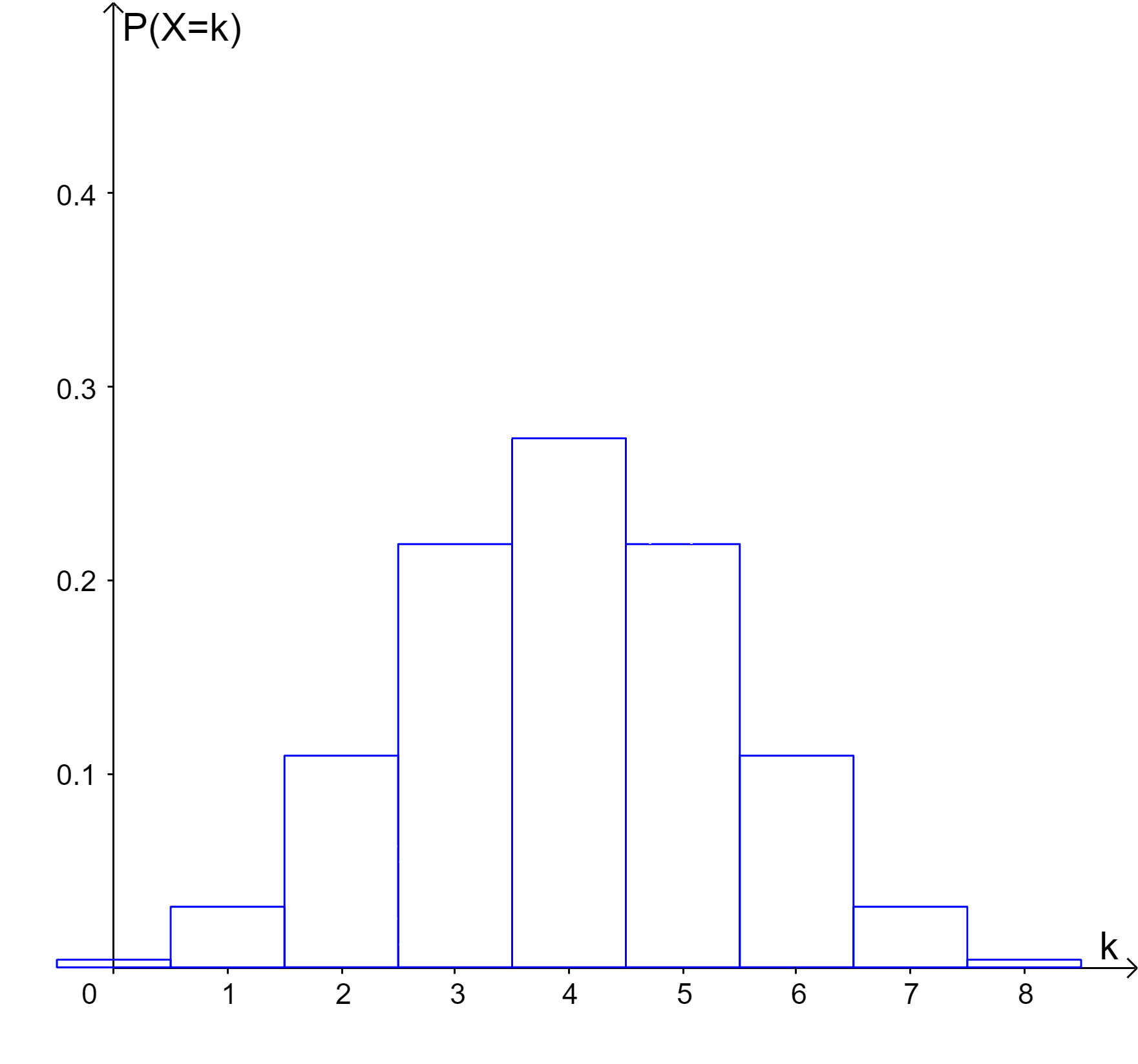 |
$n = \dots$, $p = \dots$ | $P(X = k) = \dots$ |
| (b) | 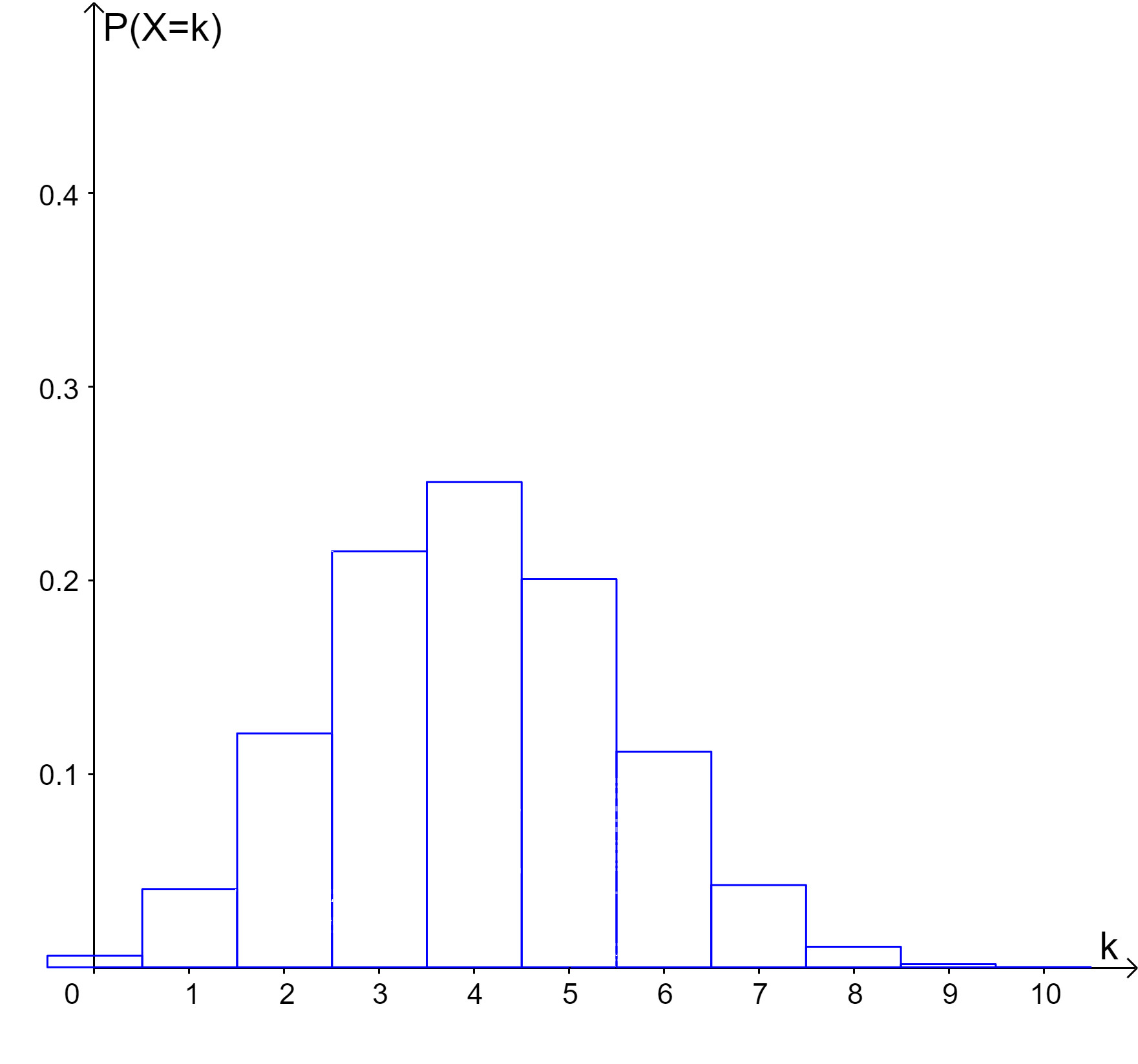 |
||
| (c) | 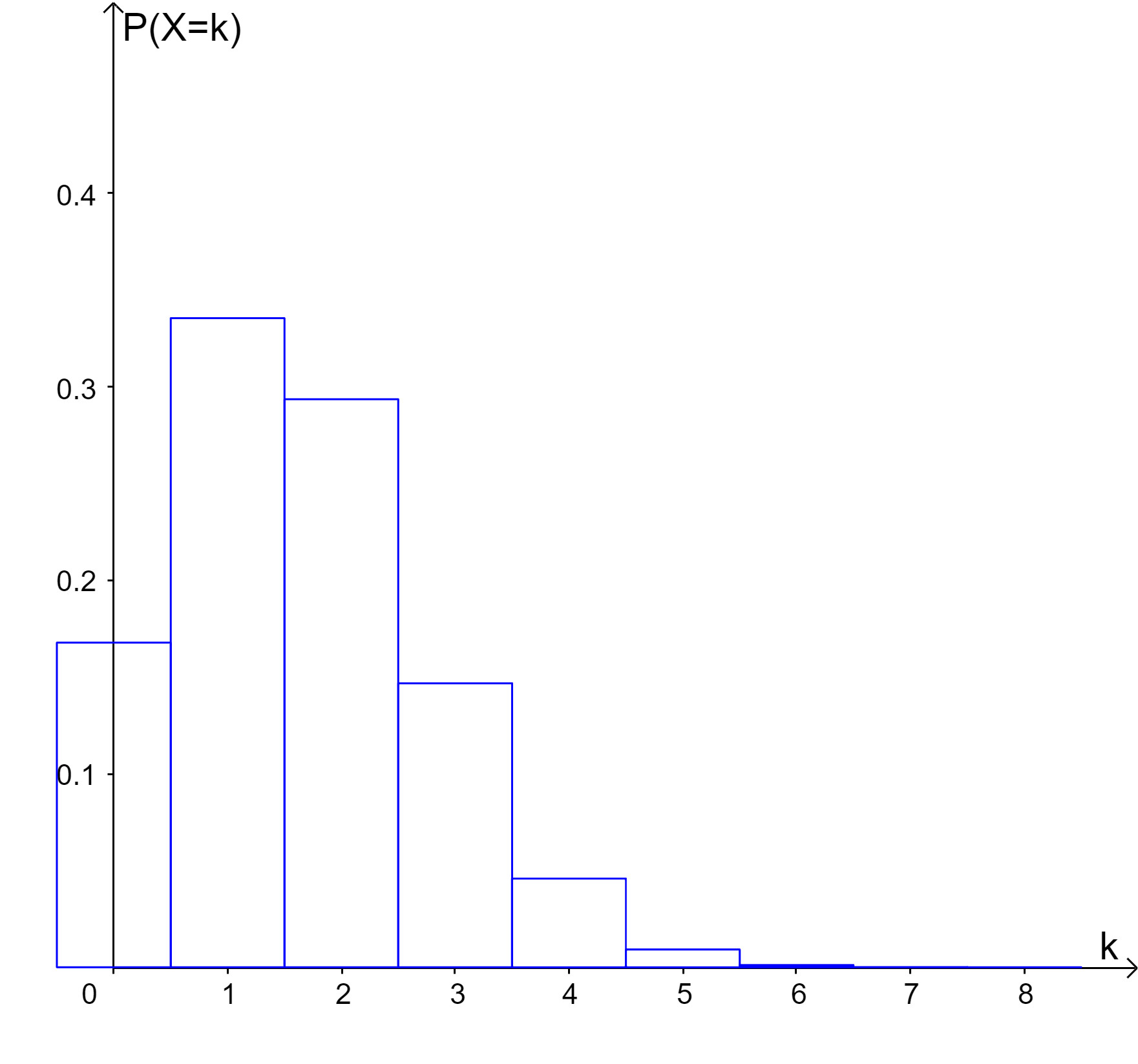 |
||
| (d) | 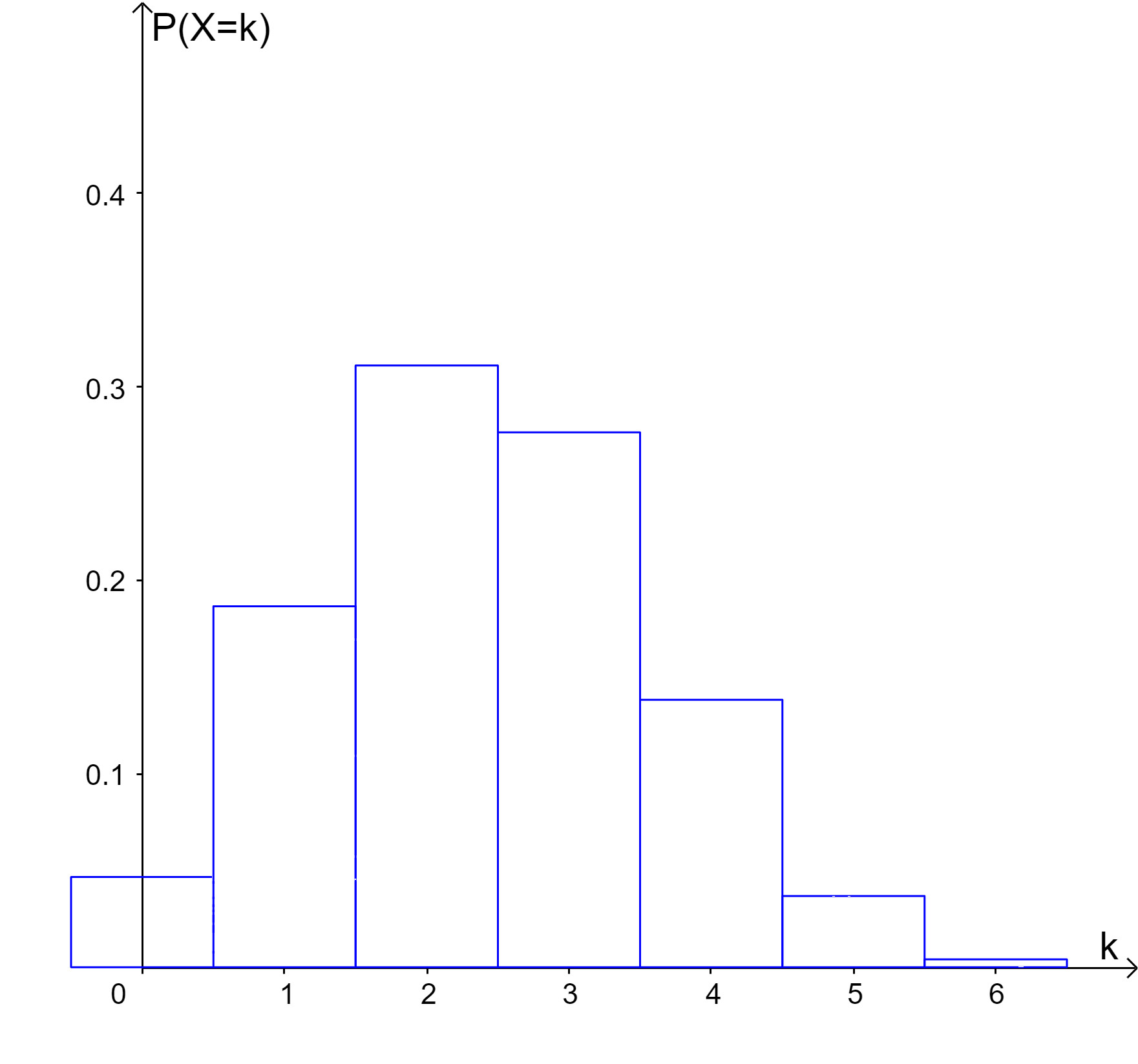 |
||
| (e) | 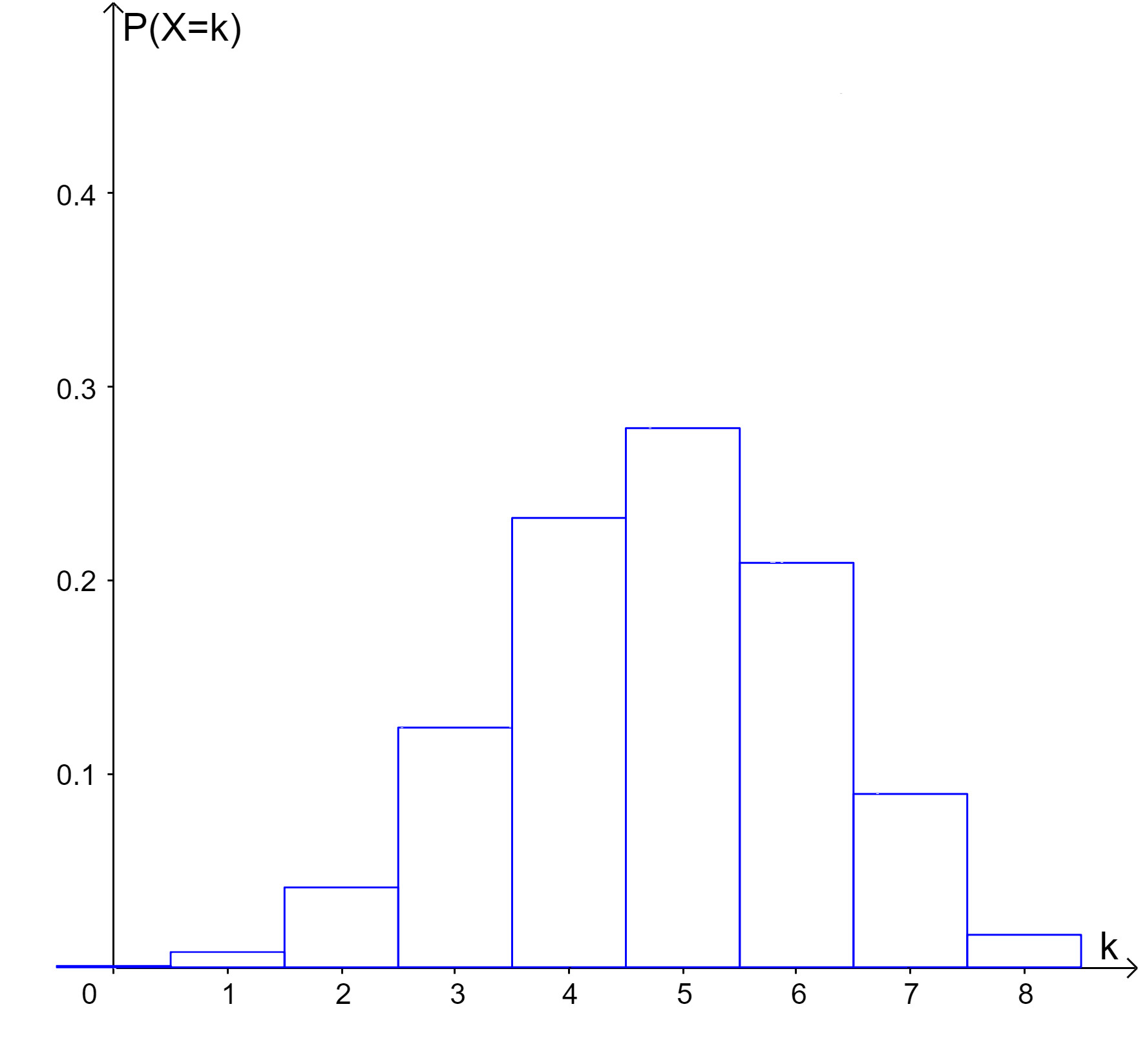 |
Ordne den Histogrammen (a) bis (e) die passenden Binomialverteilungen (1) bis (8) zu (wobei zwei Binomialverteilungen übrigbleiben). Gib in der Tabelle auch die Parameter der Binomialverteilungen an.
- $\quad P(X = k) = \binom{10}{k} \cdot 0.4^k \cdot 0.6^{10-k}$
- $\quad P(X = k) = \binom{8}{k} \cdot 0.8^k \cdot 0.2^{8-k}$
- $\quad P(X = k) = \binom{8}{k} \cdot 0.6^k \cdot 0.4^{8-k}$
- $\quad P(X = k) = \binom{8}{k} \cdot 0.2^k \cdot 0.8^{8-k}$
- $\quad P(X = k) = \binom{6}{k} \cdot 0.4^k \cdot 0.6^{6-k}$
- $\quad P(X = k) = \binom{8}{k} \cdot 0.5^k \cdot 0.5^{8-k}$
- $\quad P(X = k) = \binom{10}{k} \cdot 0.8^k \cdot 0.2^{10-k}$
- $\quad P(X = k) = \binom{6}{k} \cdot 0.6^k \cdot 0.4^{8-k}$
Aufgabe 2
Betrachte eine Binomialverteilung mit den Parametern $n = 20$ und $p = 0.7$. Stelle diese Parameter im folgenden Applet ein.
Zum Herunterladen: binomialverteilung_kumuliert1.ggb
Bestimme mit Hilfe des Applets die gesuchten Wahrscheinlichkeiten in der Tabelle.
| Ereignis - Sprechweise | Ereignis - Schreibweise | Berechnung | |
| (a) | höchstens $10$ Treffer | $P(X \leq 10)$ | $P(X \leq 10) = P(0 \leq X \leq 10) \approx \dots$ |
| (b) | weniger als $15$ Treffer | $P(X \text{ < } 15)$ | |
| (c) | mindestens $12$ Treffer | ||
| (d) | mehr als $17$ Treffer |
Aufgabe 3
Betrachte noch einmal die Binomialverteilung mit den Parametern $n = 20$ und $p = 0.7$. Stelle diese Parameter im folgenden Applet ein.
Zum Herunterladen: binomialverteilung_kumuliert_einseitig.ggb
Bestimme die gesuchten Wahrscheinlichkeiten mit dem gegebenen Applet. Dokumentiere die Rechnungen.
| Ereignis - Sprechweise | Ereignis - Schreibweise | Berechnung | |
| (a) | höchstens $10$ Treffer | $P(X \leq 10)$ | $P(X \leq 10) = \dots$ |
| (b) | weniger als $15$ Treffer | $P(X \text{ < } 15)$ | $P(X \text{ < } 15) = P(X \leq \dots) \approx \dots$ |
| (c) | mindestens $12$ Treffer | ||
| (d) | mehr als $17$ Treffer | ||
| (e) | mindestens $4$ und höchstens $9$ Treffer | ||
| (f) | mehr als $12$ und weniger als $15$ Treffer | ||
| (g) | genau $10$ Treffer |

