A/V-Verhältnis beim Würfel

Das A/V-Verhältnis betrachten

Im letzten Abschnitt hast du gesehen, dass die Oberfläche eines Würfels quadratisch und das Volumen eines Würfels kubisch wächst. Das bedeutet, dass das Volumen schneller wächst als die Oberfläche. Diesen Sachverhalt - der auch für andere Körperformen gilt - erfasst man mit dem A/V-Verhältnis. Das heißt, man bildet den Quotienten aus der Oberfläche $A$ und dem Volumen $V$.

$$Q_{W}(a) = \displaystyle\frac{A(a)}{V(a)}$$

Aufgabe 1

Begründe, dass man für den Würfel das folgende A/V-Verhältnis (in Abhängigkeit von der Kantenlänge) erhält:

$Q_{W}(a) = \displaystyle\frac{A(a)}{V(a)} = \displaystyle\frac{6}{a}$

Aufgabe 2

(a) Begründe: Je größer die Kantenlänge eines Würfels, desto kleiner ist das A/V-Verhältnis beim Würfel.

(b) Begründe: Für das Heizen (eines Würfel-Gebäudes) ist ein kleines A/V-Verhältnis günstig.

(c) Welche Schlussfolgerung sollte man aus (a) und (b) ziehen, wenn es um die Frage geht, ob man (würfelförmige) kleinere Häuser oder (würfelförmige) größere Gebäudekomplexe errichten soll?

Das A/V-Verhältnis deuten

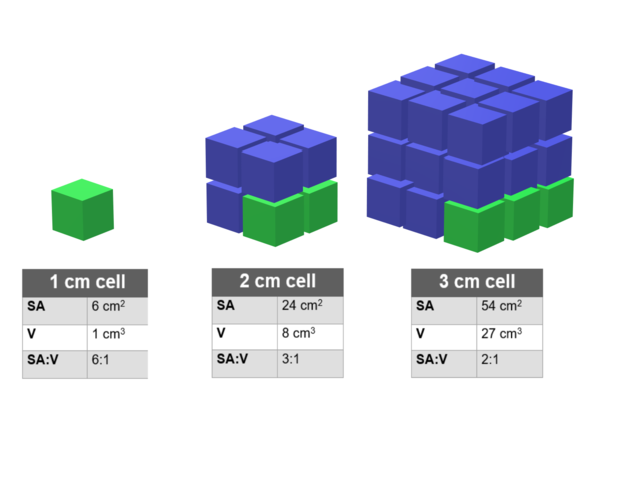
Was soll man sich unter dem A/V-Verhältnis vorstellen? Zur Klärung dieser Frage betrachten wird den Aufbau eines Würfel aus einzelnen Würfelzellen.

Aufgabe 3

Die Variable $a$ beschreibe die Kantenlänge des Würfels (in m) und damit auch die Anzahl der Würfelzellen entlang einer Kante.

Mit $V(a)$ beschreiben wir die Gesamtanzahl der Würfelzellen im Würfel mit der Kantenlänge $a$.

Mit $O(a)$ erfassen wir die Gesamtanzahl der Würfelzellen im Würfel mit der Kantenlänge $a$, die mindestens eine Fläche an der Oberfläche des Würfels haben.

(a) Vervollständige die Tabelle.

a	O(a)	V(a)	O(a) / V(a)
3	26	27	0.963
4	56	64	0.875
5
10
20
100

(b) Begründe: $O(a) = a^3 - (a-2)^3$ bzw. $O(a) = 6a^2 - 6a + 8$.

(c) Verdeutliche anhand von Zahlenwerten: Für größere $a$-Werte (z.B. $a = 20$) entspricht das Verhältnis $O(a)/V(a)$ in etwa dem A/V-Verhälnis $Q_{W}(a) = \displaystyle\frac{6}{a}$ beim Würfel. Das A/V-Verhältnis beim Würfel entspricht somit in etwa dem Anteil der Würfelzellen, die an der Oberfläche liegen, an der Gesamtanzahl der Würfelzellen.

Aufgabe 4

Verdeutliche nochmal die folgenden Begriffe und Zusammenhänge im aktuellen Kontext.

Zusammenfassung