Berechnung mit einer Lösungsformel
Die a-b-c-Formel verwenden
Wir betrachten den Fall, dass die Nullstellen einer quadratischen Funktion gesucht sind.
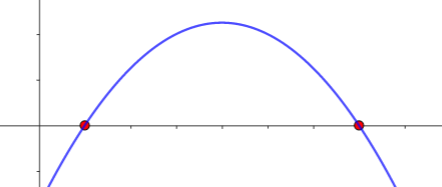
geg.: $f(x) = - x^2 + 8x - 7$
ges.: Nullstellen von $f$
Bed.: $f(x) = 0$
Wir benutzen die a-b-c-Formel:
Die quadratische Gleichung $ax^2 + bx + c = 0$ (mit $a \neq 0$) hat die Lösungen $x_{1,2} = \displaystyle{\frac{-b \pm \sqrt{b^2 - 4ac}}{2a}}$. Beachte, dass hier auch der Fall eintreten kann, dass es keine Lösung gibt, wenn eine negative Zahl unter der Wurzel vorliegt.
Mit $f(x) = \underbrace{(-1)}_{a} x^2 + \underbrace{8}_{b} x + \underbrace{(-7)}_{c}$ erhält man:
$x_{1,2} = \displaystyle{\frac{-8 \pm \sqrt{64-28}}{-2}} = 4 \pm 3$
Ergebnis: Die gesuchten Nullstellen sind $x = 1$ und $x = 7$.
Aufgabe 1
Bestimme analog die Nullstellen der folgenden Funktionen.
- $f(x) = x^2 - 5x + 4$
- $f(x) = x^2 + x -2$
- $f(x) = x^2 - 4x +4$
- $f(x) = \frac{1}{10}x^2 - \frac{3}{2}x +5$
