Ballwechsel

Einen Ballwechsel beschreiben

Zwei Tennisspieler – nennen wir sie A.A. und B.B. – tragen ein Spiel aus. Das Spielfeld sei (etwas vereinfacht) 2-mal 12 Meter lang. Wir betrachten nur den jeweiligen Abstand $s$ des Tennisballs von der Grundlinie G im Feld von A.A.. Wir betrachten also die folgende Zuordnung: Zeit [in s] -> Abstand des Balls von der Grundlinie G [in m].

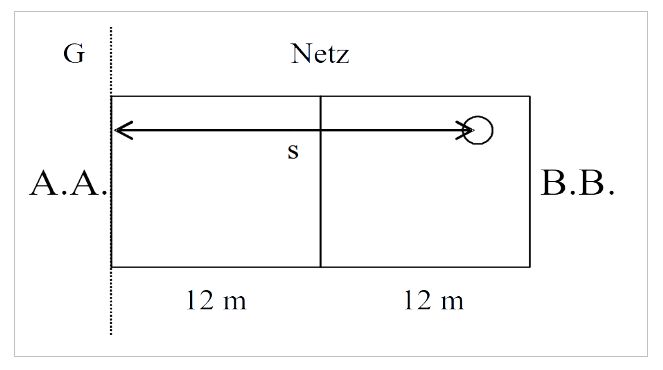
Der erste Ballwechsel lässt sich stark vereinfacht durch folgendes Weg-Zeit-Diagramm graphisch beschreiben. Auf der $x$-Achse ist hier die Zeit $t$ in Sekunden abgetragen, auf der $y$-Achse die Entfernung $s$ von der Grundlinie G („zurückgelegter Weg in Bezug auf G“) in Metern. Der Graph beschreibt die Bewegung des Balls.

Zum Herunterladen: match1.ggb

Aufgabe 1

Kläre folgende Fragen:

• Woran erkennt man, dass A.A. aufschlägt?
• Wie weit fliegt der Ball nach dem Aufschlag?
• Wo etwa könnte B.B. den Ball „returniert“ haben?
• Woran erkennt man, dass der zweite Schlag von A.A. langsamer ist als der Aufschlag?
• Was ist zum Zeitpunkt $t=3$ geschehen?
• Kann man entscheiden, wer den Ballwechsel gewonnen hat?

Aufgabe 2

Der zweite Ballwechsel verläuft wie folgt: B.B. schlägt auf. Es ist bekannt, dass B.B. einen härteren Aufschlag als A.A. hat. A.A. returniert. B.B. schlägt den Ball volley zurück, leider aber ins Aus hinter die Grundlinie. Skizziere einen Graph, der den Spielverlauf in etwa wiedergibt.

Aufgabe 3

Entwickle selbst einen (sinnvollen) Ballwechsel mit Graph und verbaler Beschreibung.

Aufgabe 4

Verdeutliche nochmal die folgenden Begriffe und Zusammenhänge im aktuellen Kontext.

Zusammenfassung