Veranschaulichung mit Spurpunkten
Spurpunkte von Ebenen
Du kennst bereits Spurpunkte von Geraden; dasselbe gibt es auch für Ebenen:
Die Spurpunkte einer Ebene sind die Schnittpunkte einer Ebene mit den Koordinatenachsen.
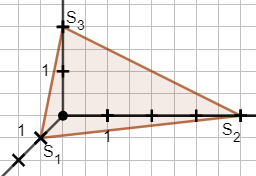
- Der Spurpunkt $S_{1}$ ist der Schnittpunkt der Geraden mit der $x_1$-Achse.
- Der Spurpunkt $S_{2}$ ist der Schnittpunkt der Geraden mit der $x_2$-Achse.
- Der Spurpunkt $S_{3}$ ist der Schnittpunkt der Geraden mit der $x_3$-Achse.
Man nutzt Spurpunkte, um eine Ebene darzustellen.
Aufgabe 1 (Einstieg)
Eigentlich kannst du schon Spurpunkte berechnen, wenn du die Definition genau betrachtest – und das ganz ohne Normalenform oder Koordinatenform.
Eine Ebenengleichung in Koordinatenform geometrisch deuten
Zielsetzung
Spurpunkte hängen eng mit den Zahlen $a, b, c, d$ in der Koordinatenform zusammen. Wir wollen nun diesen Zusammenhang erkunden.
Aufgabe 2 (Einstieg)
Überlege dir mögliche Fragestellungen rund um Spurpunkte. Welche Zusammenhänge zwischen der Koordinatenform und Spurpunkten könnte man untersuchen? Wie könnte man dafür vorgehen?
Aufgabe 3 (Erarbeitung)
Beantworte die in Aufgabe 2 gestellten Fragen mithilfe des Applets unter der Aufgabe.
Auf den kommenden Seiten dieser Lernstrecke werden verschiedene Fragestellungen vorgestellt und in Aufgaben gezeigt, wie man die Fragen beantworten kann. Ein möglicher Weg besteht also darin, nun Seite für Seite durchzugehen und wichtige Fragen zu klären. Alternativ kannst du aber auch erst selbst (am besten in einer Kleingruppe) die Fragen selbst beantworten und die weiteren Seiten nur für einen Vergleich nutzen.
Zum Herunterladen: koordinatenform3.ggb

