Normalendarstellung von Ebenen und Geraden

Worum geht es hier?

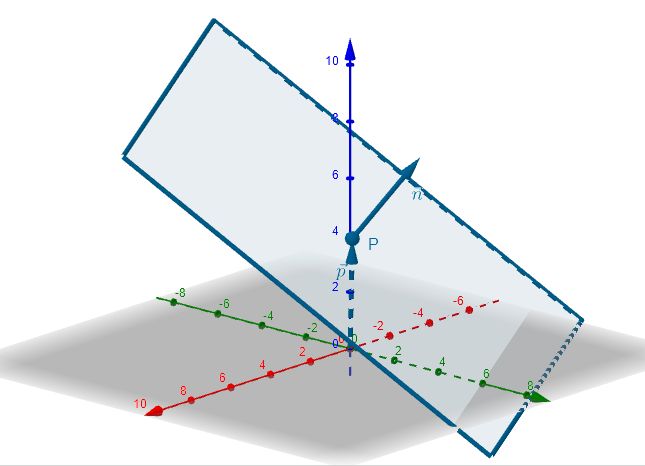
Ebenen im 3D-Raum lassen sich mit Hilfe von Ebenengleichungen in Parameterform vektoriell beschreiben. In diesem Kapitel lernst du eine weitere Möglichkeit zur vektoriellen Beschreibung von Ebenen kennen.

Für dieses Thema musst du wissen, ...

• ... wie man die Orthogonalität von Vektoren mit dem Skalarprodukt überprüft.
• ... wie man Vektoren konstruiert, die zu gegebenen Vektoren orthogonal sind.
• ... wie man eine Ebene in Parameterform angibt.

Hier lernst du, ...

• ... was ein Normalenvektor einer Ebene (bzw. einer 2D-Gerade) ist.
• ... wie man Ebenen (bzw. 2D-Geraden) mit Hilfe eines Stütz- und Normalenvektors beschreibt.

Diese Inhalte findest du hier:

1. Erkundung – Zurück zu den Solarmodulen
2. Strukturierung – Ebenengleichung in Normalenform
3. Vertiefung – Umwandlung von Ebenengleichungen
4. Übungen – Normalendarstellung von Ebenen und Geraden
5. Überprüfung – Alles klar?
6. Zusammenfassung – Normalendarstellung von Ebenen und Geraden