Übungen – Orthogonalität und Lagebeziehungen
Aufgabe 1: Lagebeziehungen untersuchen ★★
Gegeben sind die folgenden geometrischen Objekte:
$E_1 : 3x_1 + 4x_3 = 12$
$E_2 : \left[\vec{x} - \left(\begin{array}{c} 1 \\ 3 \\ 2 \end{array}\right)\right] \cdot \left(\begin{array}{c} 0 \\ 0 \\ 2 \end{array}\right) = 0$
$g : \vec{x} = \left(\begin{array}{c} 4 \\ 0 \\ 0 \end{array}\right) + t \cdot \left(\begin{array}{c} -4 \\ 3 \\ 2 \end{array}\right)$
$E_3 : \vec{x} = \left(\begin{array}{c} 4 \\ 0 \\ 0 \end{array}\right) + r \cdot \left(\begin{array}{c} -4 \\ 3 \\ 2 \end{array}\right) + s \cdot \left(\begin{array}{c} 0 \\ 0 \\ 1 \end{array}\right)$
Untersuche, welche Lagebeziehungen zwischen den Objekten jeweils vorliegt (mit Begründung). Fertige eine Skizze an, in der die Lage der Objekte zueinander verdeutlicht wird.
Aufgabe 2: Eine geometrische Konstellation erstellen ★★
Es wird dir nun eine Ebene vorgegeben und du sollst weitere geometrische Elemente finden, sodass eine bestimmte Situation vorliegt.
(a) Situation 1
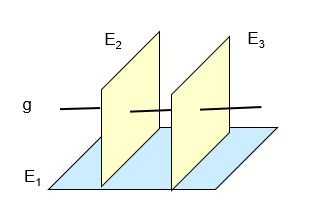
$E_1 : \left[\vec{x} - \left(\begin{array}{c} -2 \\ 1 \\ -1 \end{array}\right)\right] \cdot \left(\begin{array}{c} 2 \\ 0 \\ 1 \end{array}\right) = 0$
- $E_2$ und $E_3$ sollen orthogonal zu $E_1$ sein.
- $E_2$ und $E_3$ sollen echt parallel sein.
- $g$ soll $E_2$ und $E_3$ orthogonal schneiden.
- $g$ soll nicht in $E_1$ liegen.
(b) Situation 2
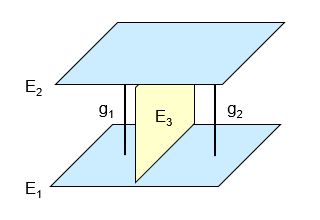
$E_1 : \left[\vec{x} - \left(\begin{array}{c} 4 \\ 0 \\ 1 \end{array}\right)\right] \cdot \left(\begin{array}{c} -1 \\ 1 \\ 2 \end{array}\right) = 0$
- $E_2$ soll echt parallel zu $E_1$ sein.
- $E_3$ soll orthogonal zu $E_1$ sein.
- $g_1$ und $g_2$ sollen $E_1$ orthogonal schneiden.
- $g_1$ und $g_2$ sollen nicht identisch sein.

