Ebene-Ebene
Zielsetzung
Hier wollen wir die Lagebeziehungen zweier Ebenen untersuchen und dafür die Bestandteile einer Ebenengleichung in Normalenform verwenden.
Aufgabe 1 (Einstieg)
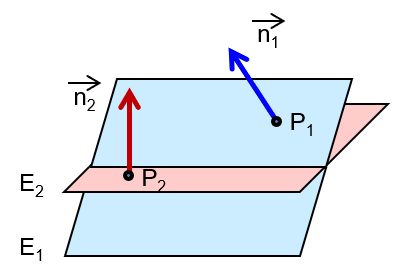
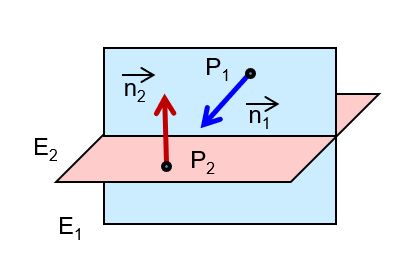
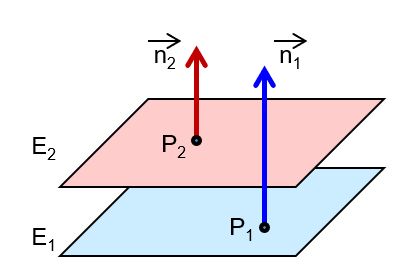
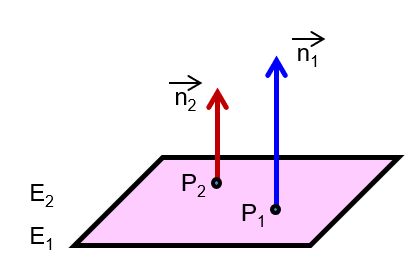
(a) Nenne die möglichen Lagebeziehungen.
(b) Vergleiche mit der nachfolgenden Liste. Es ist eine neue Lagebeziehung ergänzt. Sie ist aber nur ein Spezialfall einer bekannten Lagebeziehung. Erkläre, wovon die Rede ist.
Lagebeziehungen mit Stützpunkten und Normalenvektoren charakterisieren
Wir gehen im Folgenden davon aus, dass zwei Ebenen mit einer Ebenengleichung in Normalenform gegeben sind. Also: $E_1: [\vec{x} - \vec{p_1}] \cdot \vec{n_1} = 0$ und $E_2: [\vec{x} - \vec{p_2}] \cdot \vec{n_2} = 0$.
Aufgabe 2 (Erarbeitung; offen)
Finde für die Lagebeziehungen aus Aufgabe 1 passende Kriterien, wie die Beziehungen rechnerisch überprüfen kann. Nutze dafür die Bestandteile der Ebenengleichungen in Normalenform. Das Applet unter der Aufgabe kann dir bei der Vorstellung helfen.
💡 Hilfestellung
Es hilft, wenn du für jede Lagebeziehung ein Bild vor Augen hast:
| Lagebeziehung | Veranschaulichung | Bedingung |
|---|---|---|
| die Ebenen schneiden sich |  |
|
| die Ebenen schneiden sich orthogonal |  |
|
| die Ebenen sind echt parallel |  |
|
| die Ebenen sind identisch |  |
Zum Herunterladen: ebene_ebene2.ggb
Aufgabe 3 (Erarbeitung; geleitet)
Wir betrachten nun erst konkrete Ebenen und untersuchen diese. Damit findest du einfacher Kriterien.
Gegeben ist die Ebene $E_1$ mit einer Ebenengleichung in Normalenform:
$E_1 : \left[\vec{x} - \left(\begin{array}{c} 2 \\ 1 \\ 3 \end{array}\right)\right] \cdot \left(\begin{array}{c} 2 \\ 0 \\ 1 \end{array}\right) = 0$
Ergänze die Lagebeziehungen der Ebenen $E_1$ und $E_2$ in der Tabelle (mit kurzer Begründung). Überprüfe mit dem Applet unter der Aufgabe.
| Ebene $E_2$ | Lagebeziehung von $E_1$ und $E_2$ | Begründung |
|---|---|---|
| (a) $E_2 : \left[\vec{x} - \left(\begin{array}{c} 3 \\ 0 \\ 0 \end{array}\right)\right] \cdot \left(\begin{array}{c} 4 \\ 0 \\ 2 \end{array}\right) = 0$ | Ebenen sind parallel | $\vec{n_2} = 2\vec{n_1}$; $\vec{n_2}$ und $\vec{n_1}$ sind also parallel; $P_2$ liegt nicht in $E_1$ (überprüft mit einer Punktprobe) |
| (b) $E_2 : \left[\vec{x} - \left(\begin{array}{c} 4 \\ 2 \\ 0 \end{array}\right)\right] \cdot \left(\begin{array}{c} 1 \\ 1 \\ 1 \end{array}\right) = 0$ | ||
| (c) $E_2 : \left[\vec{x} - \left(\begin{array}{c} 2 \\ -1 \\ 4 \end{array}\right)\right] \cdot \left(\begin{array}{c} 0 \\ 1 \\ 0 \end{array}\right) = 0$ | ||
| (d) $E_2 : \left[\vec{x} - \left(\begin{array}{c} 3 \\ 1 \\ 1 \end{array}\right)\right] \cdot \left(\begin{array}{c} -2 \\ 0 \\ -1 \end{array}\right) = 0$ | ||
| (e) $E_2 : \left[\vec{x} - \left(\begin{array}{c} 3 \\ 1 \\ 2 \end{array}\right)\right] \cdot \left(\begin{array}{c} 2 \\ 0 \\ 1 \end{array}\right) = 0$ |
Zum Herunterladen: ebene_ebene2.ggb
Aufgabe 4 (Sicherung)
✏️ Fasse dir die Ergebnisse in diesem Wissensspeicher zusammen.
