Temperaturentwicklung

Aufgabe 1

Das Diagramm verdeutlicht die Erderwärmung in den letzten Jahrzehnten.

(a) Bestimme die mittlere Änderungsrate zur Temperaturentwicklung im Zeitintervall $1959 \leq t \leq 2019$. Deute das Ergebnis.

(b) Die Temperaturentwicklung unterliegt vielen Schwankungen. Verdeutliche dies, indem du die mittlere Änderungsrate für passende Zeitintervalle bestimmst. Interessant sind Phasen mit einem deutlichen Anstieg und Phasen, in denen die Temperatur wieder zurückgegangen ist.

Aufgabe 2

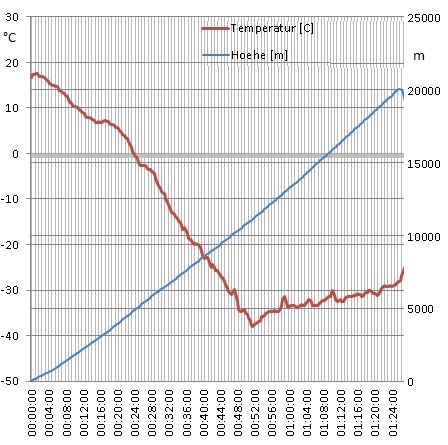
Das Diagramm zeigt Messungen von einer Ballon-Fahrt vom 27. September 2013 ab 12:40 in Stölln/Rhinow.

(a) Betrachte die Zuordnung "Zeit [min] -> Temperatur [°C]". Bestimme die mittlere Änderungsrate für diese Zuordnung im Zeitintervall $0 \leq t \leq 52$. Warum muss ein negativer Wert herauskommen? Begründe kurz.

(b) Aus dem Diagramm kann man auch die Zuordnung "Höhe [m] -> Temperatur [°C]" rekonstruieren. Bestimme die mittlere Änderungsrate für diese Zuordnung im Höhenintervall $0 \leq h \leq 10000$.

(c) Erläutere mit den beiden Aufgabenteilen: Eine Änderungsrate bezieht sich nicht immer auf eine zeitliche Entwicklung. Eine Änderungsrate bzw. Änderungsgeschwindigkeit kann auch auf eine anderen Größe bezogen werden.