Ganzrationale Funktionen vom Grad 3
Das Problem klären
Wir betrachten hier ganzrationale Funktionen vom Grad 3:
Eine ganzrationale Funktion vom Grad 3 ist eine Funktion der Gestalt $f(x) = a_3 x^3 + a_2 x^2 + a_1 x + a_0$ mit reellen Zahlen $a_3, a_2, a_1, a_0$, wobei zusätzlich $a_3 \neq 0$ vorausgesetzt wird.
Folgendes Problem wird hier bearbeitet.
Problem:
Wie sehen die Graphen ganzrationaler Funktionen vom Grad 3 aus? Haben sie immer Hoch- und/oder Tiefpunkte? Haben sie immer Wendepunkte? Wenn ja, wie viele?
Eine Argumentationsstrategie verwenden
Die im letzten Abschnitt benutzte Argumentationsstrategie lässt sich auch zur Bearbeitung des aktuellen Problems nutzen.
$f$: ganzrationale Funktion vom Grad $3$
$\Downarrow$
$f'$: ganzrationale Funktion vom Grad $2$
$\Downarrow$
Gaph $f'$: hat die Eigenschaften ...
$\Downarrow$
Gaph $f$: hat die Eigenschaften ...
Nutze diese Strategie sowie die Argumentationsbasis vom letzten Abschnitt bei der Bearbeitung der folgenden Aufgabe.
Aufgabe 1
(a) Betrachte die im Applet vorgegebene Situation. Begründe mit Hilfe der Argumentationsbasis: Die Ausgangsfunktion f hat genau einen Hoch-, Tief- und Wendepunkt. Blende Graph $f$ zur Kontrolle ein.
(b) Mit dem Schieberegler im unteren Fenster kannst du Graph $f'$ variieren. Zusätzlich kannst du den Scheitelpunkt der Parabel nach oben und unten bewegen. Es ergeben sich hierdurch verschiedene Typen von Graphen. Begründe jeweils mit Hilfe der Argumentationsbasis die Eigenschaften von Graph $f$.
Hinweis: Die $y$-Achse wurde im Applet weggelassen, da sie für die Argumentationen keine Rolle spielz. Mit dem Punkt im oberen Fenster kannst du die Lage der $x$-Achse variieren. Auch diese Lage spielt für die Argumentationen hier keine Rolle.
Zum Herunterladen: grad3.ggb
Eine Übersicht erstellen
In einer Übersicht sollen die möglichen Graphen ganzrationaler Funktionen vom Grad 3 dargestellt werden. Dabei sollen die möglichen Verläufe anhand prototypischer Beispiele verdeutlicht werden.
Aufgabe 2
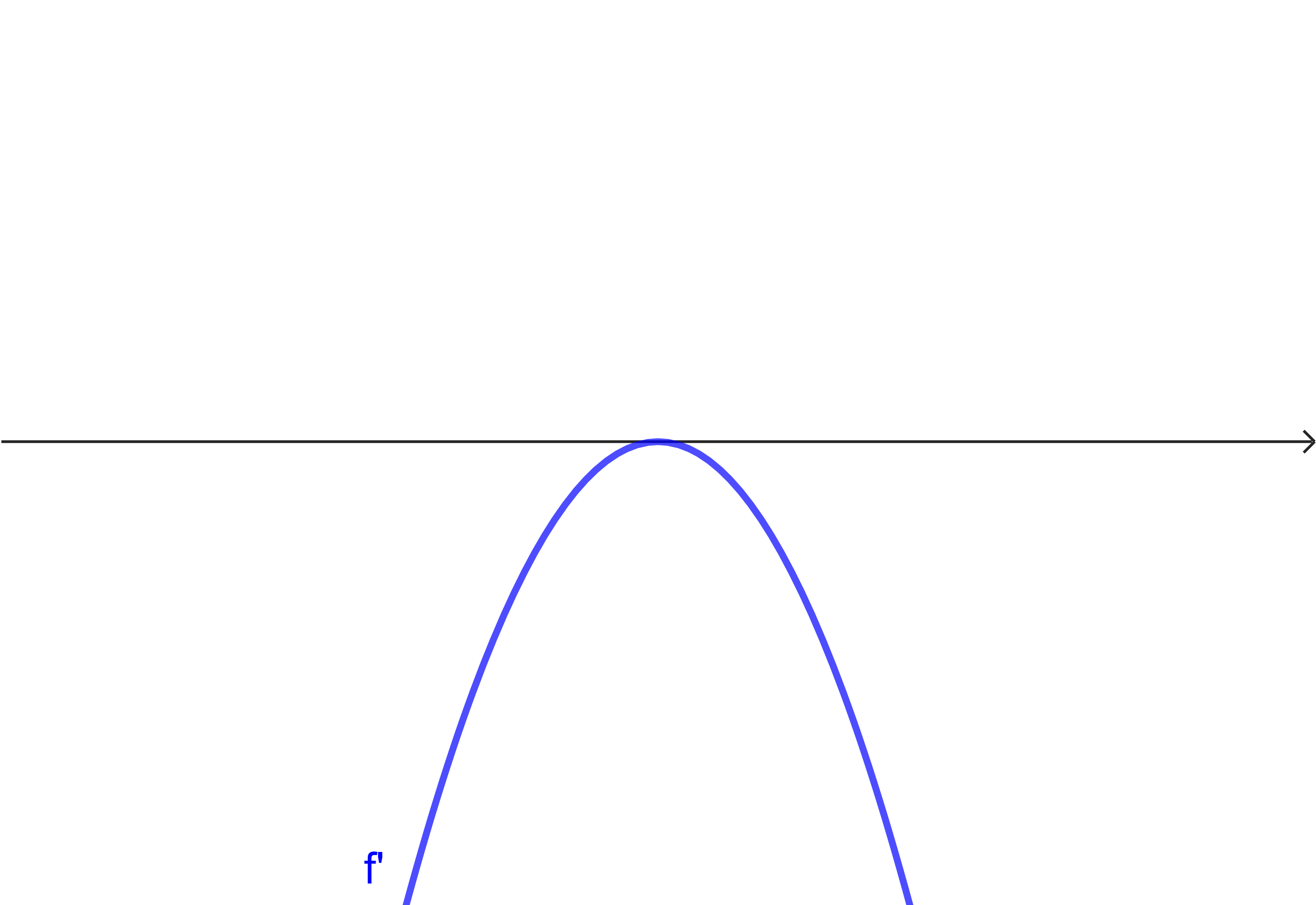
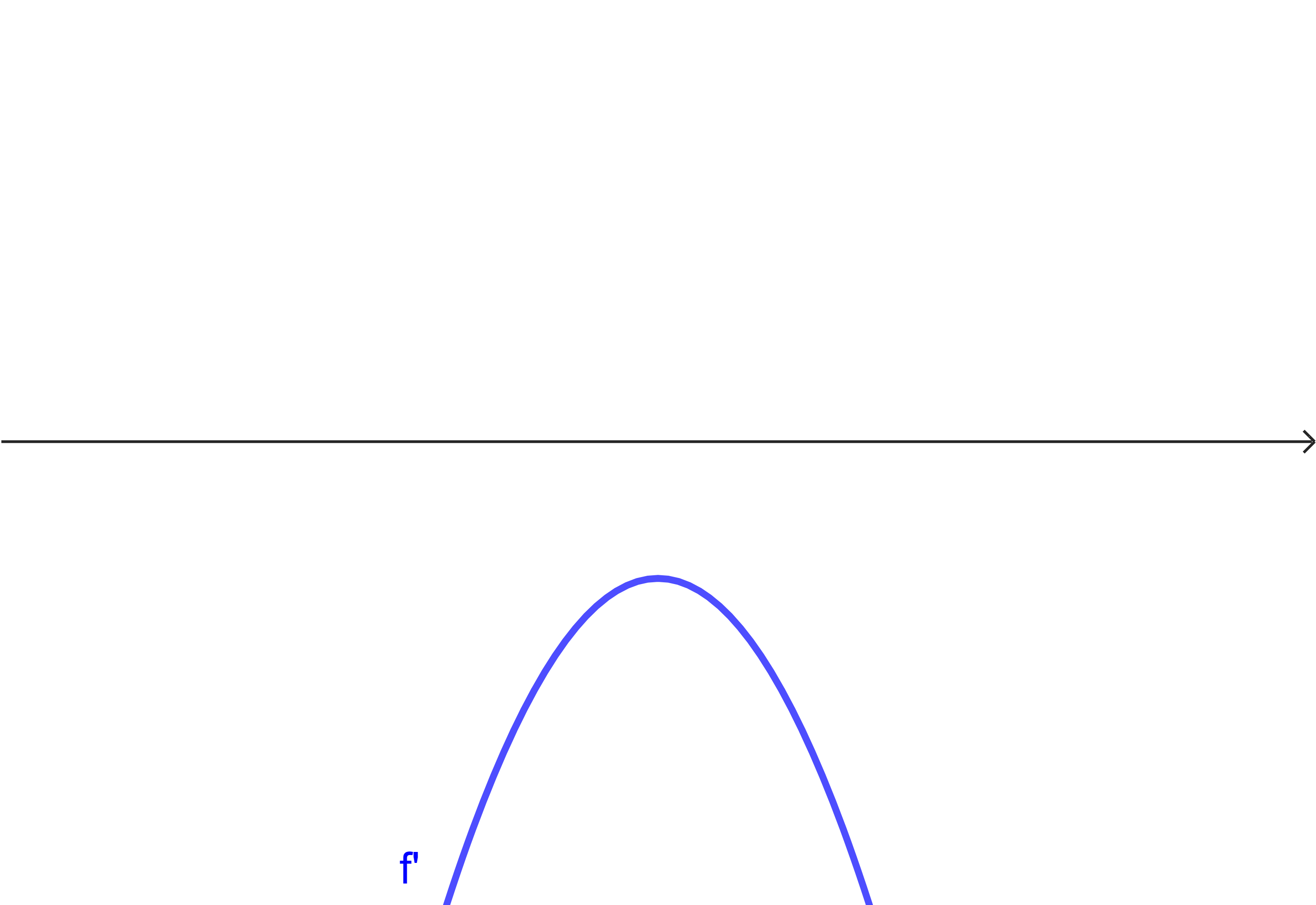
Ergänze in der Tabelle jeweils den Graph der Ausgangsfunktion $f$.
| Situation 1 | Situation 2 | Situation 3 |
 |
|
|
 |
 |
 |
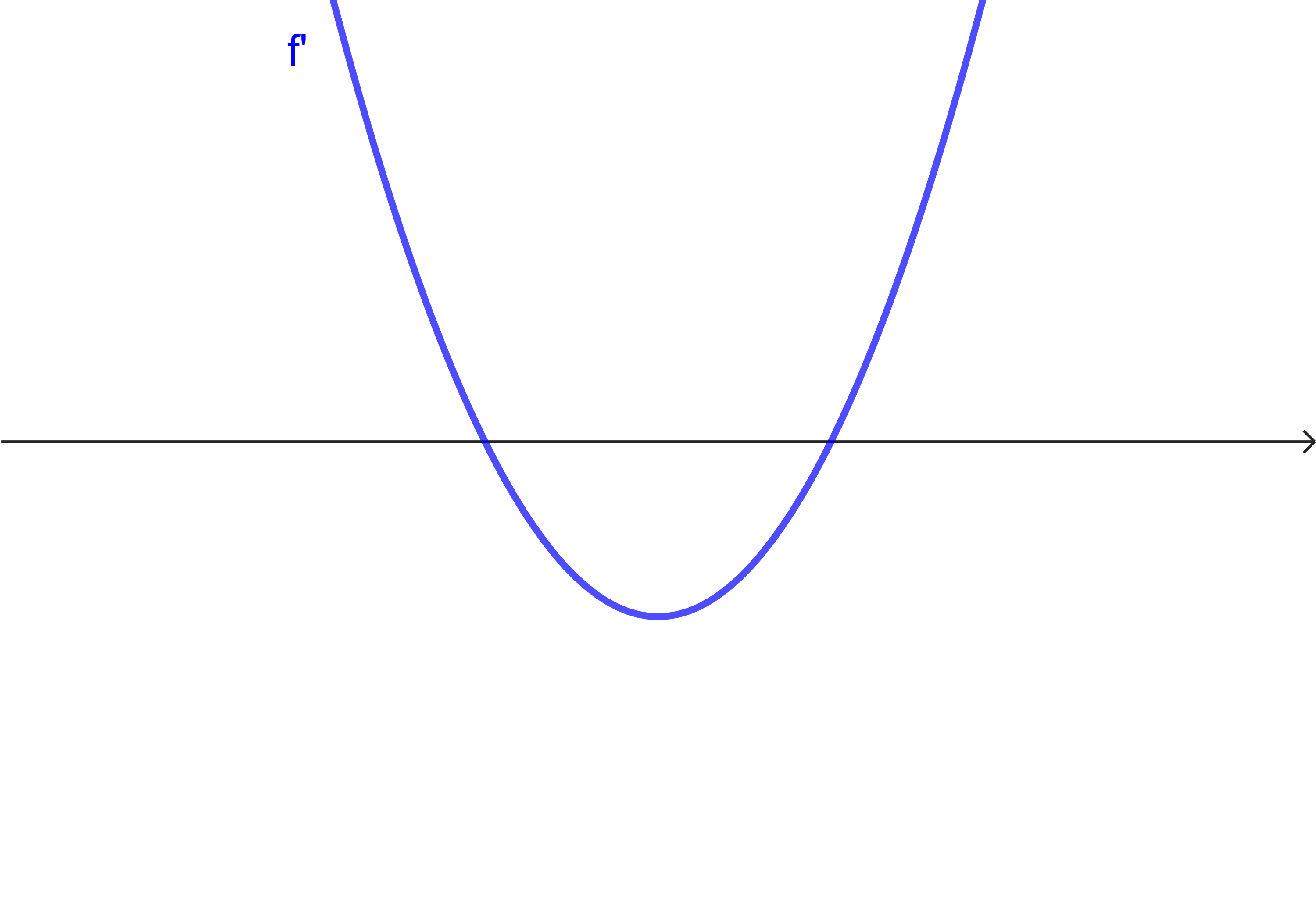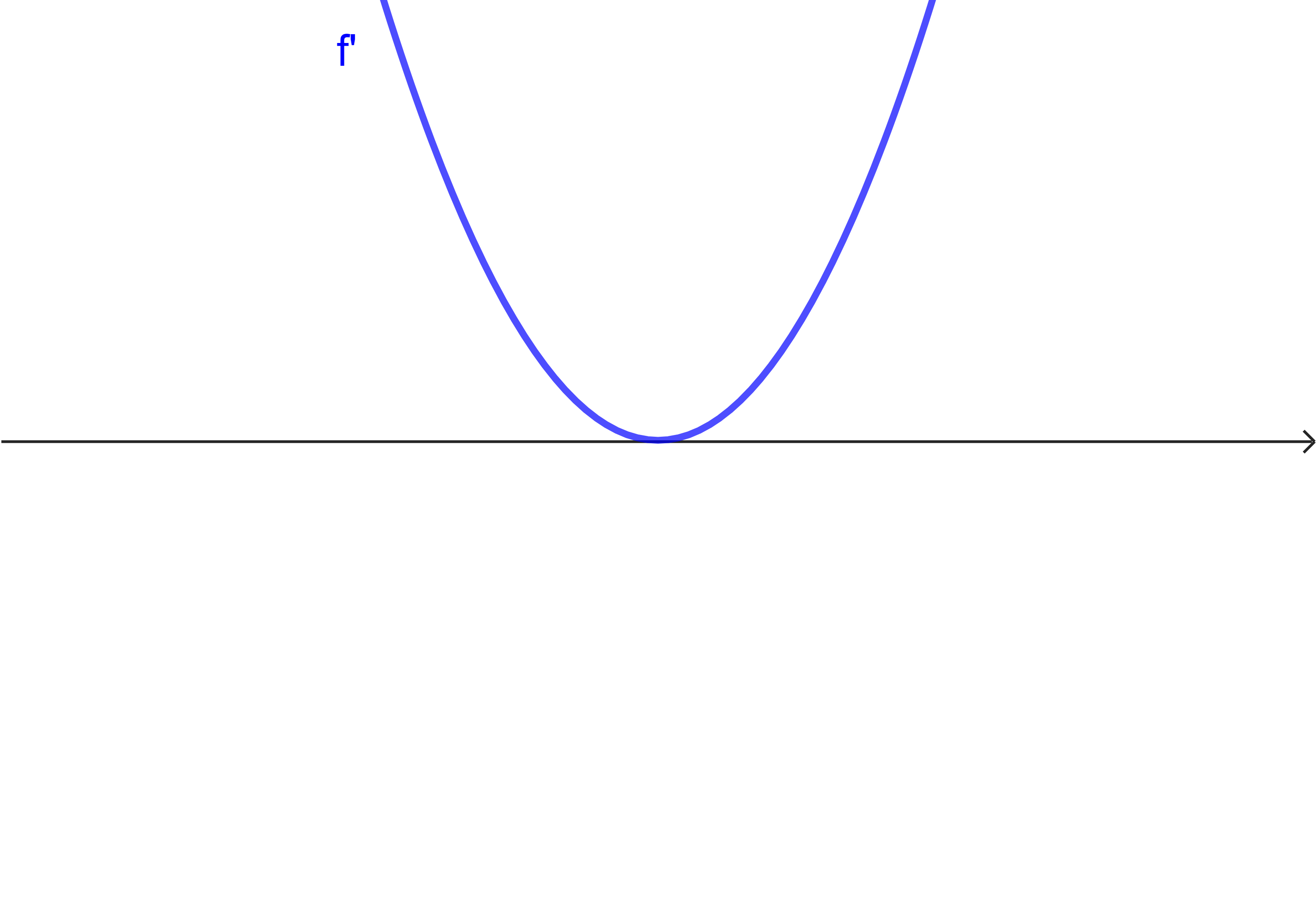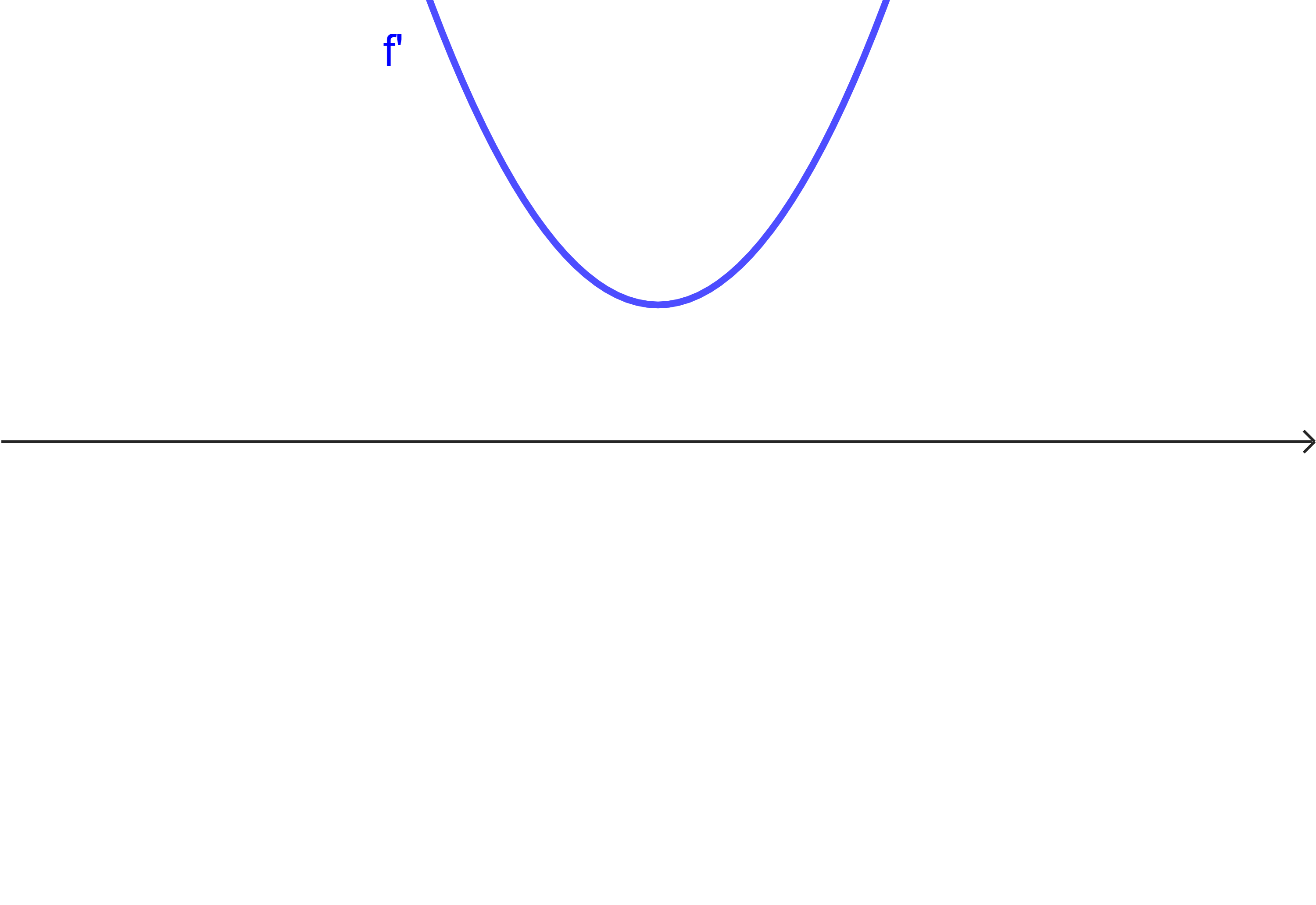| Situation 4 | Situation 5 | Situation 6 |
|
|
|
 |
 |
 |
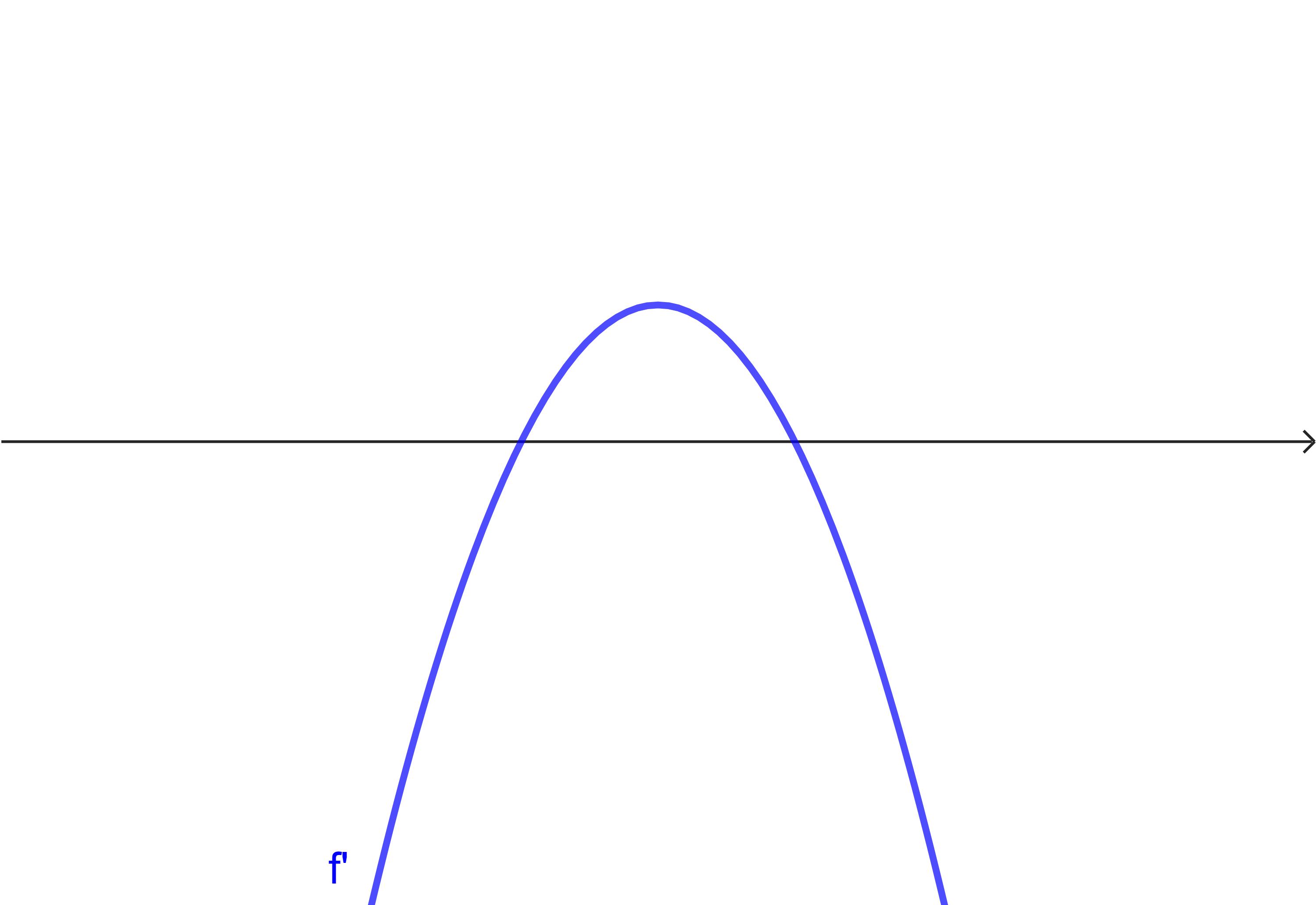Aufgabe 3
Begründe: Jede ganzrationale Funktion vom Grad 3 hat genau einen Wendepunkt.
Gib bei deiner Begründung die Argumentationsbasis an (d.h. die Zusammenhänge, auf die du dich beim Begründen beziehst).
